- 算法核心
- 代码实现
- 负权环
- 判断负权环
- 根据松弛次数
- 根据最短路径上的死循环
SPFA(Shortest Path Faster Algorithm)(队列优化)算法是求单源最短路径的一种算法。它是在Bellman-ford算法的基础上加上一个队列优化,减少了冗余的松弛操作,是一种高效的最短路算法。
Bellman-Ford算法虽然可以处理负环,但是时间复杂度为O(ne),e为图的边数,在图为稠密图的时候,是不可接受的。
Bellman-Ford算法的缺点在于,当某一个迭代求解已经获得了所有的最短路径后,它还是会继续执行没有执行完的迭代求解。但其实不用这样。
分析不难发现,起点s到某一个点的最短路径的第一条边,必定是s与s的邻接点连成的边。所以当我们在第一次松弛(即第一次迭代求解时)时,松弛的边必定包含最短路径的第一条边。
而最短路径的第二条边,必定是s的邻接点与s的邻接点的邻接点连成的边。这样以此类推。
算法核心
因此,可以对算法进行优化。设置一个队列,初始的时候将s放入队列中。
【1】队列出队,出队元素为current,松弛current与其邻接点相连的边,将松弛成功的邻接点放入队列中,这些点中包含其最短路径的第二个点(第一个点为起点)
【2】然后再次队列出队,出队元素为current,松弛current与其邻接点相连的边,但如果已在队列中就不要重复入队了
【3】重复以上步骤
其实这个步骤和无权最短路径算法有点像。
代码实现
from queue import Queue
class Edge():def __init__(self,u,v,cost):self.u = uself.v = vself.cost = cost
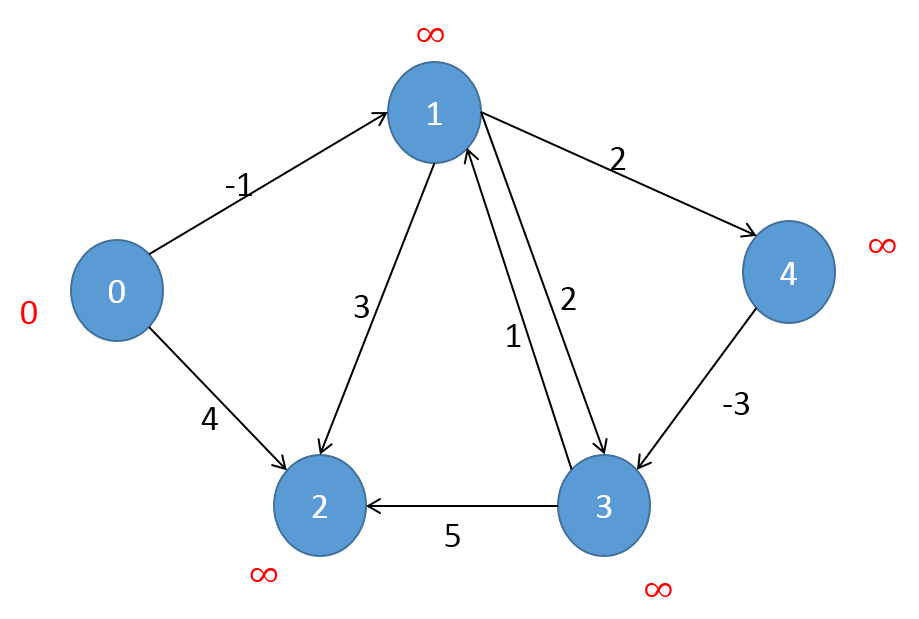
nodenum = 5edgeList = []
dis = [float("inf")]*nodenum
pre = [-1]*nodenum
know = [False]*nodenum#代表已在队列之中edgeList.append(Edge(1,4,2))
edgeList.append(Edge(0,2,4))
edgeList.append(Edge(3,2,5))
edgeList.append(Edge(3,1,1))
edgeList.append(Edge(1,3,2))
edgeList.append(Edge(4,3,-3))
edgeList.append(Edge(0,1,-1))
edgeList.append(Edge(1,2,3))edgenum = len(edgeList)original = 0
def SPFA(original):q = Queue()dis[original] = 0know[original] = Trueq.put(original)while(not q.empty()):current = q.get()know[current] = False#循环遍历current的邻接顶点for edge in edgeList:if(edge.u == current):#current点的邻接边temp = dis[edge.u] + edge.costif(temp < dis[edge.v]):#松弛操作dis[edge.v] = temppre[edge.v] = currentif(not know[edge.v]):q.put(edge.v)know[edge.v] = Trueprint('当前出队的元素为',current)print(dis)print(pre,'\n')SPFA(original)
print('\n',dis)
print(pre)
从运行结果可以看出,程序的执行过程。2出队了两次,说明它也入队了两次。从上到下观察dis数组,可以发现每个点的dis最多被更新两次,有的更新一次就更好好了。
负权环
当图中有负权环时,队列就不会有空的情况了,因为由于负权环的存在,负权环上的点就可以一直被松弛,一直能被松弛就代表着队列会不断反复让负权环上的点入队出队,程序就会死循环。
修改边的权重为:
edgeList.append(Edge(0,1,-1))
edgeList.append(Edge(1,2,3))
edgeList.append(Edge(3,1,1))
edgeList.append(Edge(1,3,2))
edgeList.append(Edge(1,4,2))
edgeList.append(Edge(0,2,4))
#edgeList.append(Edge(3,2,5))
edgeList.append(Edge(2,3,-5))
edgeList.append(Edge(4,3,-3))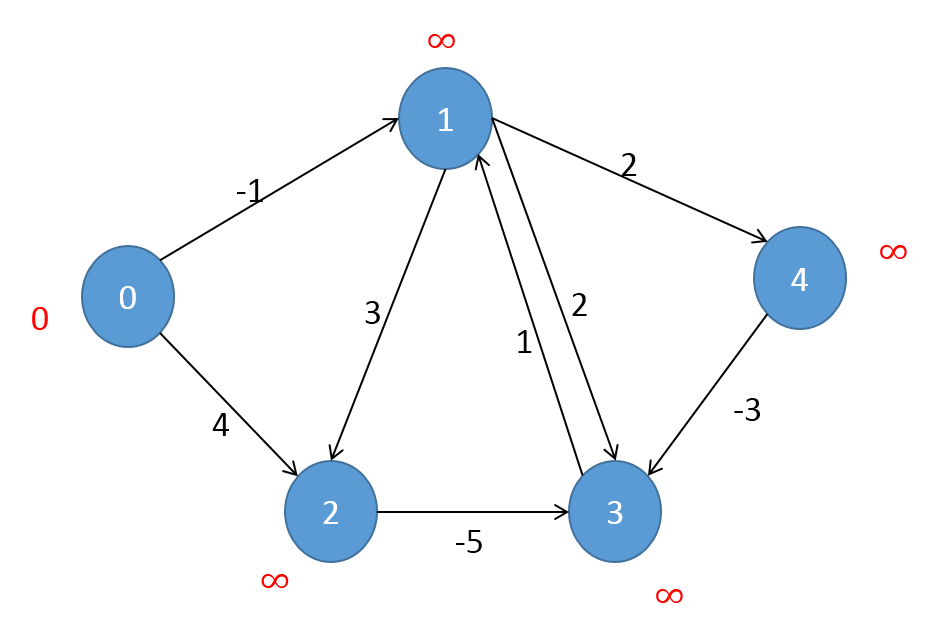
如图所示,形成了123的负权环。
此时,运行结果会无限输出,不停有元素出队入队,所以程序陷入了死循环。
判断负权环
根据松弛次数
n代表节点个数。
根据松弛次数是否大于等于n来判断负权环,是从网上其他博客说的,根据出队次数是否大于等于n来判断,想到的。因为,判断出队次数,是判断更新次数的上界。
用一个n大小的数组来代表每个点的松弛次数。因为SPFA算法里的松弛,和Bellman-ford算法里的松弛一样。Bellman-ford算法里,对同一个点的松弛次数,在极端情况下,可以想象把这些松弛次数分配到每一次迭代求解中去,而迭代求解一共只有n-1次。所以一旦某个点的松弛次数等于了n,那么就说明有负环。
所以,在每次进行松弛后,遍历判断每个点的松弛次数,如果有一个等于n(再执行下去就会大于n),就说明有负环。
#用松弛次数来判断负权环
from queue import Queue
class Edge():def __init__(self,u,v,cost):self.u = uself.v = vself.cost = cost
nodenum = 5edgeList = []
dis = [float("inf")]*nodenum
pre = [-1]*nodenum
know = [False]*nodenum#代表已在队列之中update = [0]*nodenum#代表每个点被更新的次数edgeList.append(Edge(0,1,-1))
edgeList.append(Edge(1,2,3))
edgeList.append(Edge(3,1,1))
edgeList.append(Edge(1,3,2))
edgeList.append(Edge(1,4,2))
edgeList.append(Edge(0,2,4))
#edgeList.append(Edge(3,2,5))
edgeList.append(Edge(2,3,-5))
edgeList.append(Edge(4,3,-3))edgenum = len(edgeList)original = 0
def SPFA(original):q = Queue()dis[original] = 0know[original] = Trueq.put(original)while(not q.empty()):current = q.get()know[current] = Falseflag = False#负环判断标记#循环遍历current的邻接顶点for edge in edgeList:if(edge.u == current):#current点的邻接边temp = dis[edge.u] + edge.costif(temp < dis[edge.v]):#松弛操作dis[edge.v] = temppre[edge.v] = currentupdate[edge.v] += 1for i in update:if(i==nodenum):flag =Trueprint('最后一次出队的是',current)breakif(flag == True):breakif(not know[edge.v]):q.put(edge.v)know[edge.v] = Trueif(flag == True):breakprint('当前出队的元素为',current)print(dis)print(pre,'\n')SPFA(original)
print('dis',dis)
print('pre',pre)
print('update',update)
运行结果并没有全部截图下来,因为中间执行了很多次不该有的出队入队操作(每次出队都输出东西),这里只截了最后结果。可以看到update数组中,有一个等于了5,所以程序就判断有了负权环。
而且读者可以通过所有的输出结果,统计每个点出队次数,会发现,这些点里面出队次数最大也就为4(我用画正字来记的数==)。意思就是,如果程序通过出队次数来判断的话,那么程序还得多执行几次,不该有的出队入队操作。这也证实了,判断出队次数,是判断更新次数的上界。
但通过所有输出结果,还是觉得程序判断出负权环判断得太迟了(中间执行了很多次不该有的出队入队操作),有没有一种更快的方法,可以及早判断出负权环呢。答案是有,如下。
根据最短路径上的死循环
寻找最短路径的方法是通过pre数组:
比如代码实现章节的程序运行后,pre数组为[-1, 0, 1, 4, 1],要寻找从起点0到3的最短路径,步骤如下:
【1】记录下3,路径为=>3
【2】记录下pre[3]=4,路径为=>4=>3
【3】记录下pre[4]=1,路径为=>1=>4=>3
【4】记录下pre[1]=0,路径为=>0=>1=>4=>3
【4】记录下pre[0]=-1,遇到-1,到达终点,返回路径=>0=>1=>4=>3
从起点到某点的最短路径,路径上的点必定都是不重复的。但当有负权环时,这句话就不成立了。
比如负权环章节的程序运行后,pre数组为[-1, 3, 1, 2, 1],寻找从起点0到3的最短路径,会发现,上述步骤会一种进行下去,因为到达不了终点,死循环了(虽然这里程序是用的递归)。
#此程序用pre数组的死循环来判断是否有负环
from queue import Queue
class Edge():def __init__(self,u,v,cost):self.u = uself.v = vself.cost = cost
nodenum = 5edgeList = []
dis = [float("inf")]*nodenum
pre = [-1]*nodenum
know = [False]*nodenum#代表已在队列之中edgeList.append(Edge(0,1,-1))
edgeList.append(Edge(1,2,3))
edgeList.append(Edge(3,1,1))
edgeList.append(Edge(1,3,2))
edgeList.append(Edge(1,4,2))
edgeList.append(Edge(0,2,4))
#edgeList.append(Edge(3,2,5))
edgeList.append(Edge(2,3,-5))
edgeList.append(Edge(4,3,-3))edgenum = len(edgeList)original = 0def if_circle(pre):#判断是否有负权环,返回真假,如有负权环,并返回环prev = -1#设置环的起点circle = []#记录负权环def get(i):circle.append(i)if(i == -1):#到达了正常的终点,判断无负权环return Falseif(i == prev):#到达了不该达到的终点,判断有负权环return Truereturn get(pre[i])for i in pre:if(i == -1):#超出索引限制了continueprev = iif(get(pre[i])):#传入参数直接是i的上一个顶点,直接传入i会出错return (True,circle)circle.clear()return (False,)def SPFA(original):q = Queue()dis[original] = 0know[original] = Trueq.put(original)while(not q.empty()):current = q.get()know[current] = Falseflag = False#循环遍历current的邻接顶点for edge in edgeList:if(edge.u == current):#current点的邻接边temp = dis[edge.u] + edge.costif(temp < dis[edge.v]):#松弛操作dis[edge.v] = temppre[edge.v] = currentif(if_circle(pre)[0]):print('有负环为',if_circle(pre)[1])print(dis)print(pre)flag = Truebreakif(not know[edge.v]):q.put(edge.v)know[edge.v] = Trueif(flag == True):breakprint('当前出队的元素为',current)print(dis)print(pre,'\n')SPFA(original)
print('\n',dis)
print(pre)
通过这种方式,程序可以很快地判断出来负权环(程序只出队了4次就判断出来了)。且得到了负权环的组成的点[2, 1, 3]。