算法思想：

        我们用数组记录每个结点的最短路径估计值，用邻接表来存储图G。

        采取的方法是动态逼近法：

        1、设立一个先进先出的队列用来保存待优化的结点。

        2、优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在当前的队列中，就将v点放入队尾。

        3、这样不断从队列中取出结点来进行松弛操作，直至队列空为止

        因为这个反复松弛的过程使得spfa算法可以求带有负权边的最短路问题，这是与Dijkstra的主要区别

---

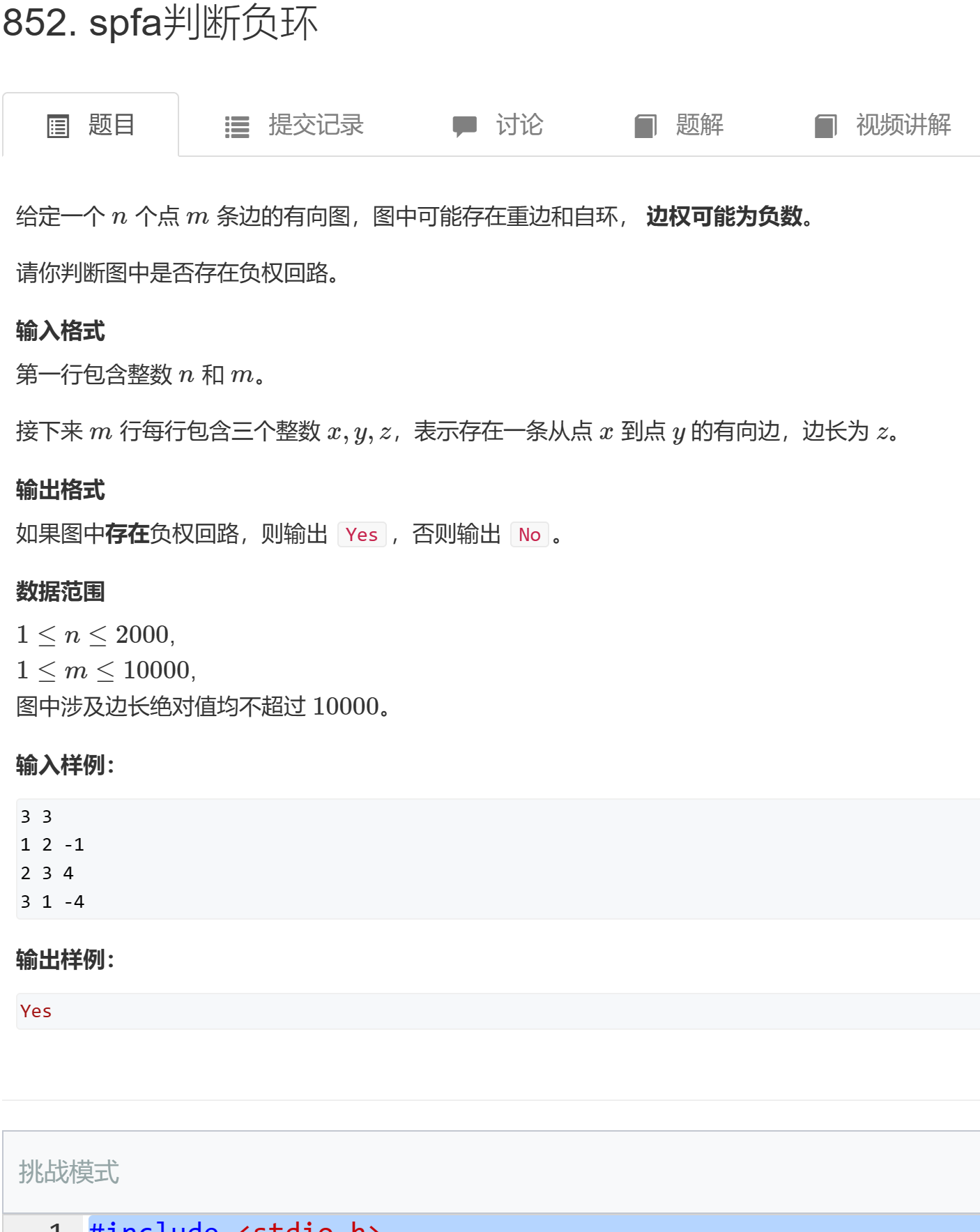
 求负环

        如下图所示的一个图，我们可以轻易发现2,3,4三个节点之间的边组成了一个负环，在spfa算法的迭代中，如果出现了负环会陷入死循环，给一个通俗的解释，要求节点1到节点5的最短距离，如果是1--2--3--5的路线，那么距离是10，显然1--2--3--4--2--3--5 这条路线距离变成了8，所以，为了达到最短路，会在2,3,4之间永远循环下去，所以这个性质就是用来判断最短路的依据

 

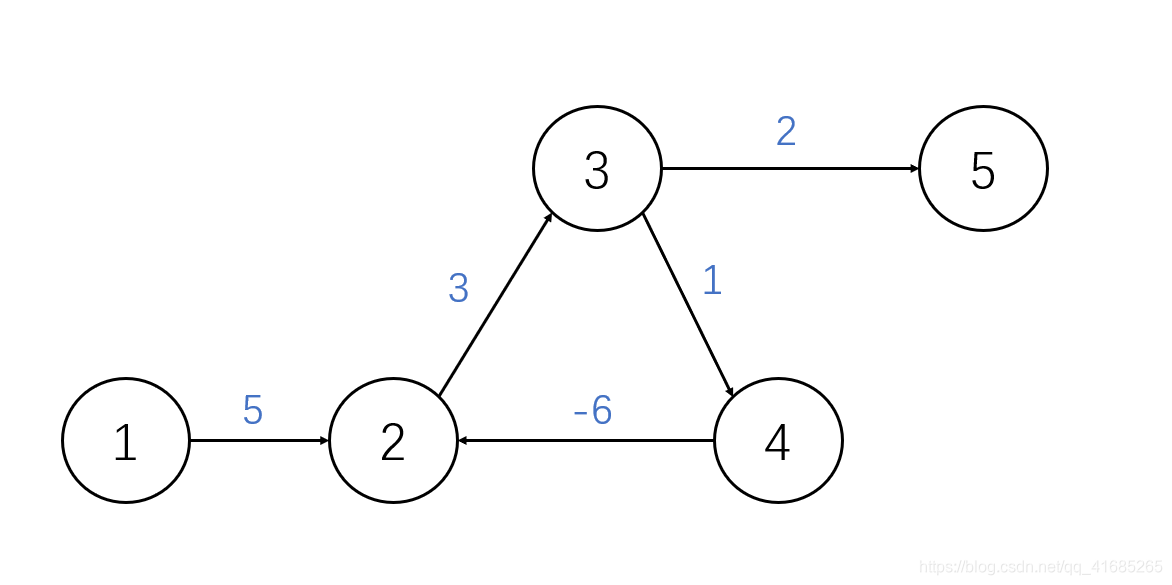
        如果不存在负环的话，每个节点可以通过其他节点作为中间节点然后再到达该节点来进行松弛，所以每个节点最多松弛n次，因此只要某个节点进入队列了超过了n次，那必定存在负环！

 

代码

以该题为例，这是一个最简单的判负环问题：https://www.acwing.com/problem/content/854/

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>using namespace std;
const int N=10010;
int h[N],e[N],ne[N],idx,w[N];
int dist[N];
bool st[N];int n,m;int cnt[N];
void add(int a,int b,int c){e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}int spfa(){memset(dist,0x3f,sizeof dist);dist[1]=0;queue<int>q;for(int i = 1;i<=n;i++)q.push(i),st[i] = true;st[1]=true;while(q.size()){int t = q.front();q.pop();st[t] = false;for(int i = h[t];i!=-1;i = ne[i]){int j = e[i];if(dist[j]>dist[t]+w[i]){dist[j] = dist[t]+w[i];cnt[j] ++; //可以优化为cnt[j] = cnt[t] + 1;if(cnt[j]>=n)return 1;if(!st[j]){q.push(j);st[j] = true;}}}}return 0;
}int main(){cin>>n>>m;memset(h,-1,sizeof h);while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);}int t=spfa();if(t==1)cout<<"Yes";else cout<<"No";return 0;
}