适用情景
SPFA算法一般运用在求最短路问题当中的单源最短路中存在负权边的情况(正权边如果出题人没有特别恶心去卡的话,也是ok的),SPFA算法还可以去判断图中是否存在负环。
时间复杂度
一般来讲是O(m),m就是图当中的边数,最坏的情况是O(nm)。
算法解释 I (SPFA求单源最短路)
首先是对于图的存储,可以用邻接表去存储图,也可以用邻接矩阵去存储图。这边就不像之前的Bellman-Ford算法,那个算法的话对于边的存储十分的随意,因为每一次循环的话,我只要保证能够遍历到每一条边就可以。而在SPFA算法当中,不能去随便的遍历所有边,详情见下。还有add函数的话也是会的吧,值得注意的是这边有个小坑的地方,对于h的初始化-1,这一步的操作必须放在插入边之前,这看似是小儿科,但是这个错误我感觉还是很容易犯。
#define N 100010
int h[N];
int e[N];
int ne[N];
int w[N];
int idx;
void add(int a, int b, int c)
{e[idx]=b;ne[idx]=h[a];h[a]=idx;w[idx]=c;idx++;
}
memset(h,0xff,sizeof(h));然后当然也得创建一个dist数组,用来存储每一个点到一号点之间的最短路距离,在初始化的时候,默认每一个点都是无穷大(当然,一号点除外)。
int dist[N];
memset(dist,0x3f,sizeof(dist));
dist[1]=0;还要创建一个队列,这个队列就是来记录当前有哪些点到一号点的最短路距离已经是被更新过了的,那些最短路距离已经被更新过了的点就是要放到队列里面,然后这些受到更新的点再去更新其他点的最短路距离,然后那些点等会儿也会进到队列里面,如此往复。当然在最初始状态,很容易就知道一号点到一号点的最短路距离就是0,因此可以理解成一号点已经被更新过了,所以最开始一号点先入队。
int queue[N];
int hh;
int tt;
queue[0]=1;那等会儿在具体的算法过程中,该如何去判断有哪些点已经是被更新过了(或者说通俗来讲的话,就是说有哪些点已经是在这个队列里面),这时候你只需要去再创建一个数组st,就是做标记作用,标记一下有哪些点已经是在队列里面。当然,一号点的话到一号点的距离就是0,所以说也相当于是更新过了它的最短路距离,所以在最初始状态的话,我们知道一号点是入队了的,所以在这边标记的时候,得给一号点标记一下,说明他此时已经在队列里面了。
int st[N];
st[1]=1;必须要弄懂的是:SPFA算法的精髓就在于:一旦我该点的最短路被更新了是吧(相当于别人恶心了我,那我也就去恶心别人,并且恶心一遍接触到的人之后,我就悄咪咪滚蛋了,队头元素开始去恶心别人),我就去更新我所连接到的那些图当中的点的最短路距离,其实就是去判断dist[ b ]与dist[ a ]+c (从a指向b,权重为c)。遍历一边以该点为出发点的所有边,遍历一圈之后,该点就从队头弹出,然后在遍历的过程当中,如果有点的最短路距离被我更新了,那么此时此刻他如果不在队列里面的话,那就入队,在的话那就不说了。就这样循环往复,到最后队列为空为止。
while(hh<=tt)
{int num=queue[hh];hh++;st[num]=0;for (int i=h[num];i!=-1;i=ne[i]){int k=e[i];if (dist[k]>dist[num]+w[i]){dist[k]=dist[num]+w[i];if (st[k]==0){st[k]=1;queue[++tt]=k;}}}
}然后在最后,如果说等到队列都空了,此时此刻dist[ n ]还是不动如山如之前初始化一模一样,这就说明是从一号点是走不到n号点的
if (dist[n]==0x3f3f3f3f)
{printf("impossible\n");
}
else
{printf("%d\n",dist[n]);
}例题
来源:AcWing
851. spfa求最短路 - AcWing题库

#include <stdio.h>
#include <string.h>
#define N 100010
int n,m;
int h[N];
int e[N];
int ne[N];
int w[N];
int idx;
void add(int a, int b, int c)
{e[idx]=b;ne[idx]=h[a];h[a]=idx;w[idx]=c;idx++;
}
int dist[N];
int queue[N];
int hh;
int tt;
int st[N];
int main()
{memset(h,0xff,sizeof(h));memset(dist,0x3f,sizeof(dist));dist[1]=0;queue[0]=1;st[1]=1;scanf("%d %d",&n,&m);int a,b,c;while(m--){scanf("%d %d %d",&a,&b,&c);add(a,b,c);}while(hh<=tt){int num=queue[hh];hh++;st[num]=0;for (int i=h[num];i!=-1;i=ne[i]){int k=e[i];if (dist[k]>dist[num]+w[i]){dist[k]=dist[num]+w[i];if (st[k]==0){st[k]=1;queue[++tt]=k;}}}}if (dist[n]==0x3f3f3f3f){printf("impossible\n");}else{printf("%d\n",dist[n]);}return 0;
}算法解释 II (SPFA判断图中是否有负环)
首先必须弄清楚负权边与负环的概念,负环是一种特殊的负权边,也就是说这条边的权重是负的,并且从自己这个点出发,结果还是指向自己这个点。
SPFA算法的精髓在于:如果受到更新,就入队;然后等着去更新别人,遍历自己势力范围一圈后,出队;其他点也一样,如果受到更新,就入队
图的邻接表存储,道理还是一样的
#define N 2020
#define M 10010
int h[N];
int e[M];
int ne[M];
int w[M];
int idx;
memset(h,0xff,sizeof(h));
void add(int a, int b, int c)
{e[idx]=b;ne[idx]=h[a];h[a]=idx;w[idx]=c;idx++;
}这边与之前的SPFA算法求最短路有一些区别,首先对于队列,在初始状态就把所有的点全部放到队列里面(因为如果只放一个点的话,可能这个负环不在以该点为起点的路途网中)。那既然在最初状态所有的点都在队列当中,所以说对于标记数组st而言,所有的元素值最初都为1
int st[N];
int queue[10000000];
int hh;
int tt=-1;
for (int i=1;i<=n;i++)
{queue[++tt]=i;st[i]=1
}由于现在每一个点好像似乎都成为了“起点”,所以dist数组中的值最初全为0
int dist[N];这边还得额外定义一个cnt数组,这个数组表示在以某一点为终点的最短路当中整个路当中的边的总数量,由于现在每一个点好像似乎都成为了起点,所以在最短路当中可以理解为从自己走向自己,那么边数为0,所以一开始cnt的值全为0.
int cnt[N];然后接下来就是通过循环去执行SPFA算法的精髓,什么时候第一个if条件会进去呢,只要这时候存在负权边(a, b, c c<0 ),这时候就会去更新dist[ b ]。与此同时,最短路走通,在原先的基础之上又多加了一条边, cnt[ b ] = cnt [ a ] + 1 。如果单单是负权边倒还问题不大,如果说这时候是负环,也就意味着当我出队,但是我又把自己给更新了,于是乎我又马上又入队了,然后到时候我又出队,然后我又入队,如此循环往复,但是每一次的话cnt都会加1,直到有一天cnt大于n了,说明在最短路当中从起点到该点有n条边,那么就意味着有n+1个点,那么就意味着必然存在环,最短路,最短路,正环不可能,也就是说存在着负环
while(hh<=tt)
{int num=queue[hh];st[num]=0;hh++;for (int i=h[num];i!=-1;i=ne[i]){int k=e[i];if (dist[k]>dist[num]+w[i]){dist[k]=dist[num]+w[i];cnt[k]=cnt[num]+1;if (cnt[k]>n){printf("Yes\n");return 0;}if (st[k]==0){st[k]=1;queue[++tt]=k; }}}
}
printf("No\n");例题
来源:AcWing
852. spfa判断负环 - AcWing题库
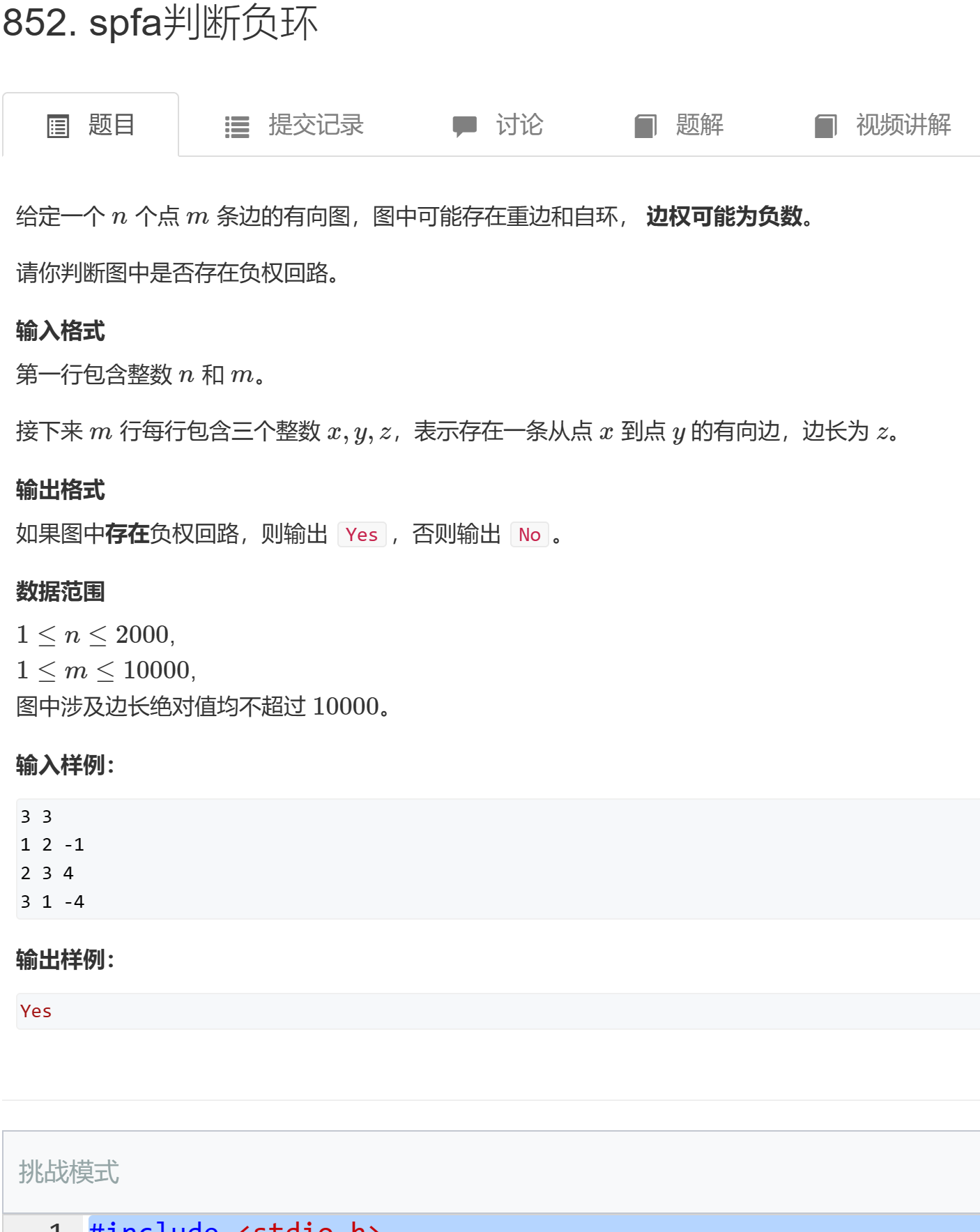
#include <stdio.h>
#include <string.h>
#define N 2020
#define M 10010
int n,m;
int h[N];
int e[M];
int ne[M];
int w[M];
int idx;
int cnt[N];
void add(int a, int b, int c)
{e[idx]=b;ne[idx]=h[a];h[a]=idx;w[idx]=c;idx++;
}
int st[N];
int queue[10000000];
int hh;
int tt=-1;
int dist[N];
int main()
{scanf("%d %d",&n,&m);memset(h,0xff,sizeof(h));int a,b,c;while(m--){scanf("%d %d %d",&a,&b,&c);add(a,b,c);}for (int i=1;i<=n;i++){queue[++tt]=i;st[i]=1;}while(hh<=tt){int num=queue[hh];st[num]=0;hh++;for (int i=h[num];i!=-1;i=ne[i]){int k=e[i];if (dist[k]>dist[num]+w[i]){dist[k]=dist[num]+w[i];cnt[k]=cnt[num]+1;if (cnt[k]>n){printf("Yes\n");return 0;}if (st[k]==0){st[k]=1;queue[++tt]=k; }}}}printf("No\n");return 0;
}