题目地址

https://leetcode-cn.com/problems/sudoku-solver/

题目描述：解数独

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

空白格用 ‘.’ 表示。

示例：

一个数独。

答案被标成红色。

Note:

1. 给定的数独序列只包含数字 1-9 和字符 ‘.’ 。
2. 你可以假设给定的数独只有唯一解。
3. 给定数独永远是 9x9 形式的。

解答

方法一：枚举法。

对于每个格子，可以填入 1 ~ 9 个数字，共有 9 * 9 个格子，因此一共有 9^{81} 种组合方法。

将上述组合方法列举出来，选择满足条件的一个即可。

上述方法虽然理论上可行，但运行时间太大，现实中不可能使用该方法。

方法二：dfs + 回溯

我们将 9 个“宫”按照以下标记划分：

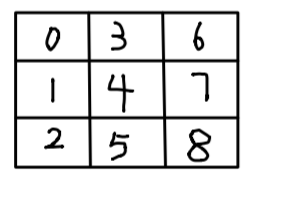
首先遍历数组，记录每组/每行/每宫中已经出现的数字，并据此求出每行/每列/每宫中可以放置的数字，将其存入哈希表中。

例如：

第一行还能放置的数字有：1,2,4,6,8,9;

第三列还能放置的数字有：1,2,3,4,5,6,7,8,9;

第一宫还能放置的数字有：1,2,4,7.

随后开始 dfs, 对于每一个没有放置数字的格子，依次检查是否可以放置数字 1~9, 若可以放置，则放置该数字，并在对应的哈希表中删去该数字。若不能放置，则证明需要回溯。

例如：在上例中，对于位置 [0,3], 依照哈希表，我们可以将 1,2,4 三个数字放入其中。

什么时候需要回溯？

例如：

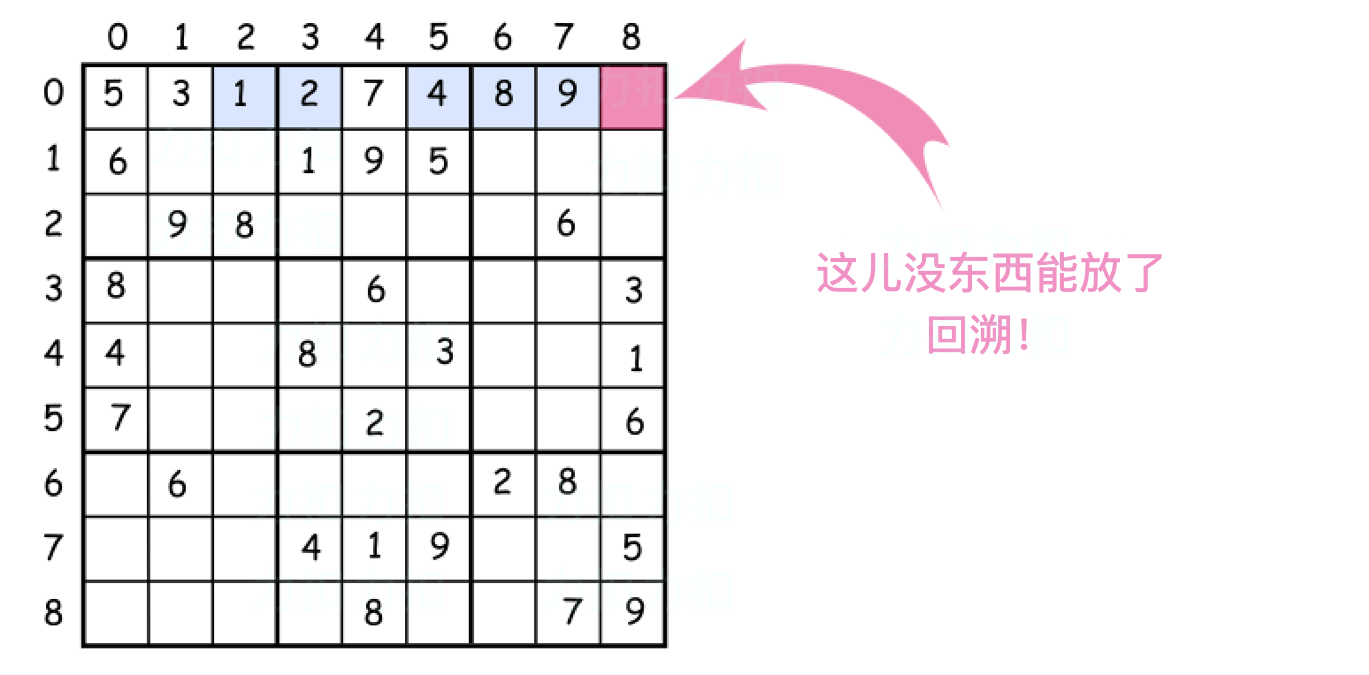
在 [0,8] 位置上, 已经无元素可放（元素 ‘6’ 不能放在这里，因为第 8 列/ 第 6 块 已经存在元素 ‘6’），此时需要回溯。这时证明之前的放置序列并不正确，我们在此时 return 出当前函数（即返回上一层递归中）。

即返回到 [0,7] 位置处，对于 1 ~ 9, 已经遍历到 ‘9’, 因此此处也不能放置除 ‘9’ 以外的数字，再返回上一层。

在 [0,6] 位置处，可以放置 ‘8’ 和 ‘9’, 由于 ‘8’ 已经证明不可行，因此尝试放置 ‘9’.

以上过程即回溯。

代码：

class Solution {
public:// line, column, block 分别存储每行、每列、每宫中可用的数字vector<set<int>> line, column, block;//哈希更新每行/列/宫中可以使用的数字void update( vector<vector<char>>& board){set<int> compare = {1,2,3,4,5,6,7,8,9};//a 行；b 列；c 宫for( int i = 0; i < 9; i++)line.push_back( compare), column.push_back( compare), block.push_back( compare); for( int i = 0; i < 9; i++)for( int j = 0; j < 9; j++)if( board[i][j] != '.'){int t = board[i][j] - '0';line[i].erase( t),  column[j].erase(t), block[i / 3 + j / 3 * 3].erase(t); }return ;}//检查该位置处字符是否可以放到该处bool check( vector<vector<char>>& board, const int& i, const int& j, int num){if( line[i].find( num) != line[i].end()&& column[j].find( num) != column[j].end()&& block[i/3 + j/3*3].find( num) != block[i/3 + j/3*3].end())return true;return false;}//标记int flag = 0;//dfs + 回溯void dfs( vector<vector<char>>& board, int count){if( count == 81){flag = 1;return ;}int i = count / 9, j = count % 9;if( board[i][j] == '.'){//检查 1 ～ 9 中数字哪一个可以放入该位置for( int k = 1; k < 10; k++)if( check( board, i, j, k)){line[i].erase( k), column[j].erase( k), block[ i /3 + j/3*3].erase( k);board[i][j] = k + '0';dfs( board, count + 1);if( !flag){line[i].insert( k), column[j].insert( k), block[ i /3 + j/3*3].insert( k);board[i][j] = '.';}elsereturn ;}}elsedfs( board, count + 1);return ;}void solveSudoku(vector<vector<char>>& board) {update( board);//show( line, column, block);dfs( board, 0);}
};

代码拆开看有点长且繁琐，若把函数拿出来单独看：

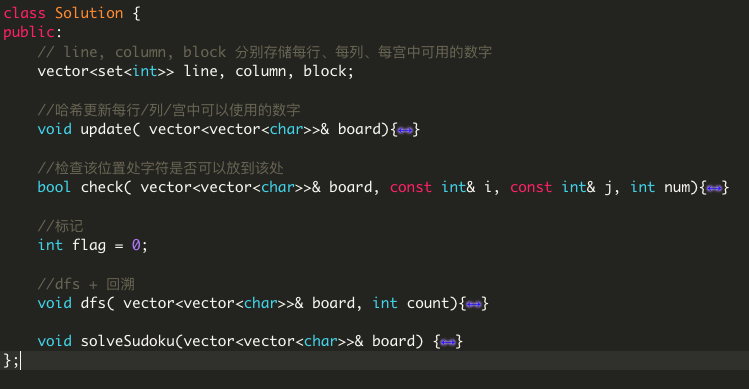
这样就好多了（自我感觉写的很好看，不接受反驳/批评）