使用java解数独

article/2025/10/2 1:27:24

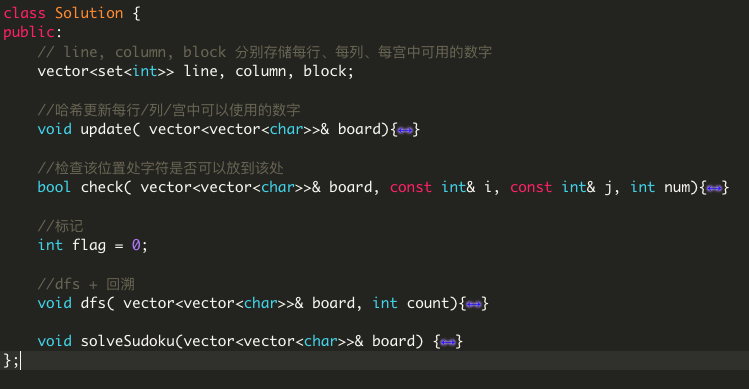
说明

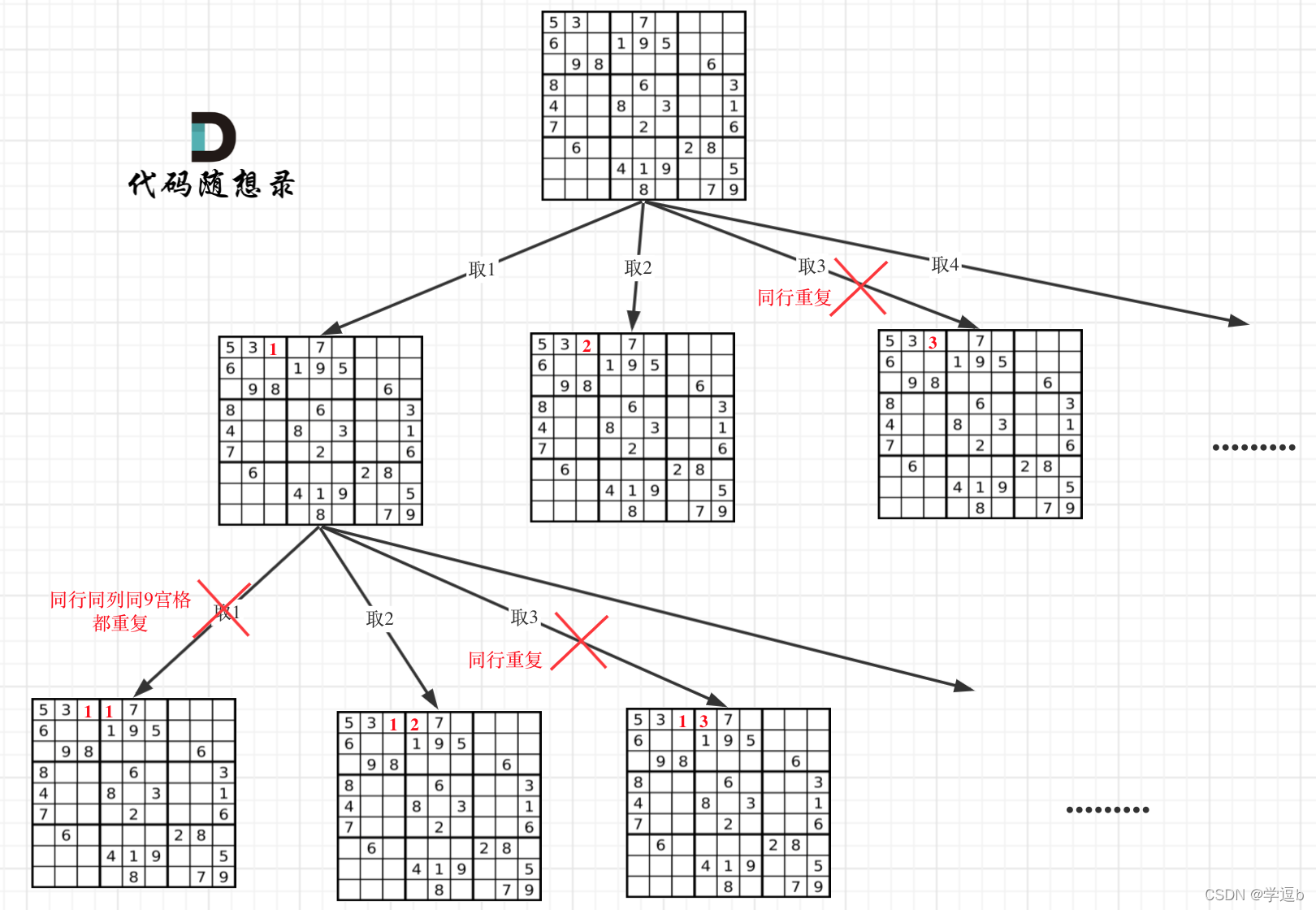
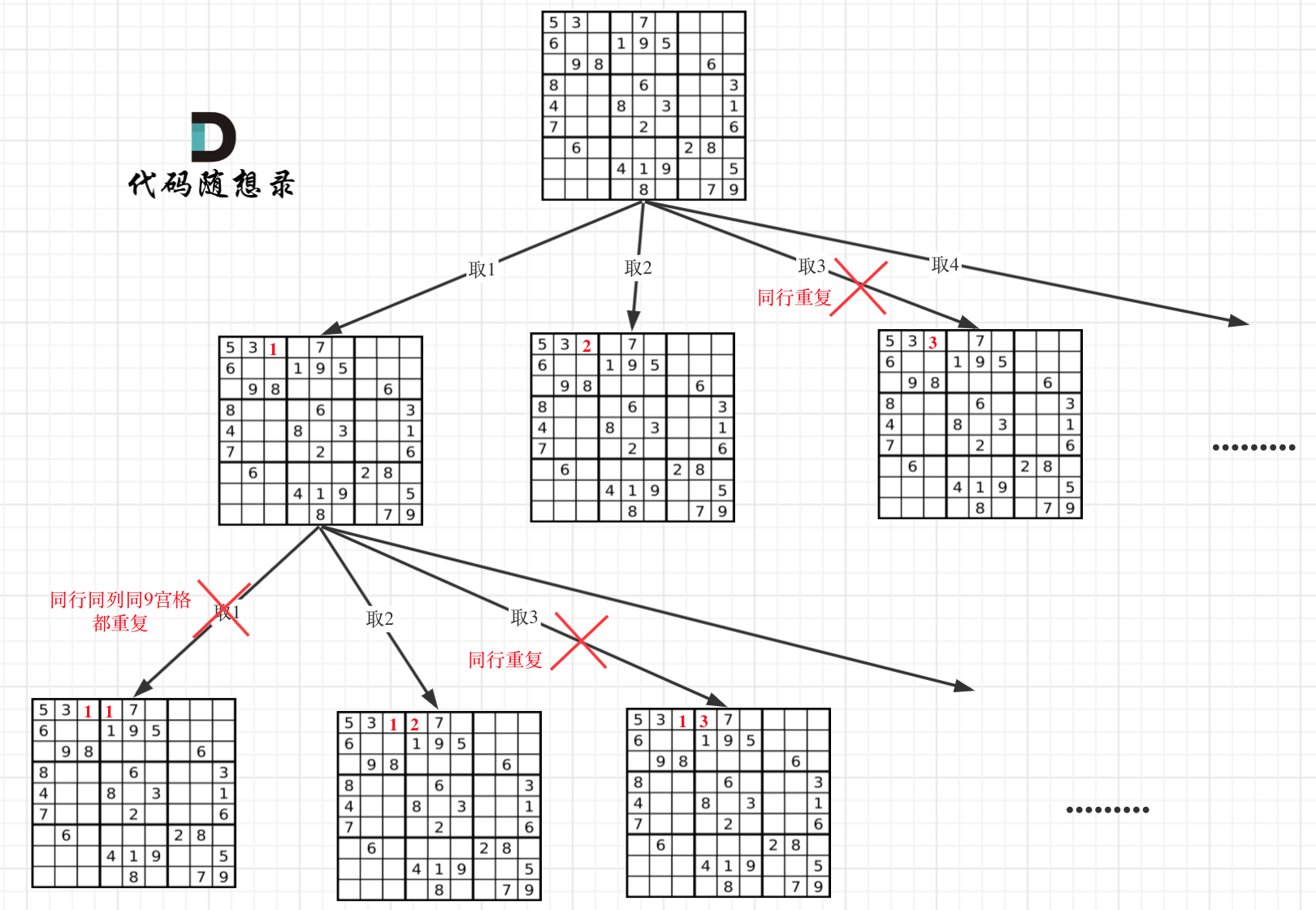
  • 先根据规则解数独,
    • 规则1: 如果备选数字只有一个, 那么就填入这个数字
    • 规则2: 如果在3*3单元格中, 或者一行, 或者一列中, 某个备选数字在所有的备选数字中只出现了一次, 那么就填入这个数字.
  • 再暴力破解数独, 依次填入备选数字, 如果不能解开, 换下一个备选数字, 直到数独完全解开.

代码

package com.example.springboot01;import org.junit.Test;
import org.junit.platform.commons.util.StringUtils;import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
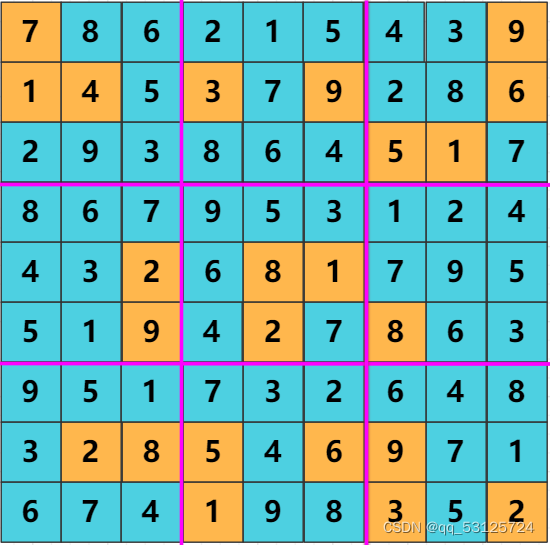
import java.util.Set;public class Test0805 {/*** 解数独* @param board 待解数独*/public void solveSudoku(char[][] board) {// 存储备选数字,全部都是null时,表示数独完全解析出来了String[][] newBoard = new String[9][9];// 统计备选数字solveSudoku1(board, newBoard);// 使用规则1和规则2解数独boolean isContinue = true;while (isContinue) {isContinue = solveSudoku2(board, newBoard) || solveSoduko3(board, newBoard);}// 暴力破解数独, 破解速度和备选数字的先后排序有很大关联int result = checkSodukoState(newBoard);if (2 == result) {solveSudoku4(0, 0, board, newBoard);}printStringArr(newBoard);}/*** 统计备选数字* @param board 待解数独* @param newBoard 剩余备选数字*/public void solveSudoku1(char[][] board, String[][] newBoard) {// 初始化备选数字for (int i = 0; i < 9; i++) {for (int j = 0; j < 9; j++) {if ('.' == board[i][j]) {newBoard[i][j] = "123456789";}}}// 从备选数字中排除掉确定数组for (int i = 0; i < 9; i++) {for (int j = 0; j < 9; j++) {if ('.' != board[i][j]) {cleaNum(i, j, board[i][j]+"", newBoard);}}}}/*** 使用待选数字排除法,直到待选数字只剩一个* @param board 待解数独* @param newBoard 剩余备选数字*/public boolean solveSudoku2(char[][] board, String[][] newBoard) {boolean isContinue = false;// 使用待选数字排除法,直到待选数字只剩一个for (int i = 0; i < 9; i++) {for (int j = 0; j < 9; j++) {if ('.' == board[i][j] && newBoard[i][j].length() == 1) {char item = newBoard[i][j].charAt(0);board[i][j] = item;newBoard[i][j] = null;isContinue = true;// 清除备选数字cleaNum(i, j, item + "", newBoard);}}}return isContinue;}/*** 清除行,列,3*3单元格内的指定备选数字* @param i 行* @param j 列* @param item 待清除数字* @param newBoard 备选数字*/private void cleaNum(int i, int j, String item, String[][] newBoard) {// 清除备选数字// 3*3单元格起始坐标(左上角)int blockRow = (i / 3) * 3;int blockCol = (j / 3) * 3;for (int m = 0; m < 9; m++) {// 清除掉行里面的备选数字itemif (newBoard[i][m] != null) {newBoard[i][m] = newBoard[i][m].replace(item, "");}// 清除掉列里面的备选数字itemif (newBoard[m][j] != null) {newBoard[m][j] = newBoard[m][j].replace(item, "");}// 清除掉3*3单元格里面的备选数字itemint x = blockRow + (m/3);int y = blockCol + (m%3);if (newBoard[x][y] != null) {newBoard[x][y] = newBoard[x][y].replace(item, "");}}}/*** 一个3*3单元格,一行或者一列的所有备选数字中,如果某个数只出现了一次,那么这个数就是最终数字* @param board 待解数独* @param newBoard 剩余备选数字* @return 是否成功解开一个数字*/private boolean solveSoduko3(char[][] board, String[][] newBoard) {boolean isContinue = false;// 行for (int i = 0; i < 9; i++) {Map<Character, Integer> numToRegion = new HashMap<>();Map<Character, Integer> map = new HashMap<>();for (int j = 0; j < 9; j++) {if (newBoard[i][j] != null) {char[] chars = newBoard[i][j].toCharArray();for (char item : chars) {numToRegion.put(item, j);if (map.containsKey(item)) {map.put(item, map.get(item) + 1);} else {map.put(item, 1);}}}}for (char item : map.keySet()) {if (map.get(item) == 1) {isContinue = true;int j = numToRegion.get(item);board[i][j] = item;newBoard[i][j] = null;// 清除备选数字cleaNum(i, j, item+"", newBoard);}}}// 列for (int j = 0; j < 9; j++) {Map<Character, Integer> numToRegion = new HashMap<>();Map<Character, Integer> map = new HashMap<>();for (int i = 0; i < 9; i++) {if (newBoard[i][j] != null) {char[] chars = newBoard[i][j].toCharArray();for (char item : chars) {numToRegion.put(item, i);if (map.containsKey(item)) {map.put(item, map.get(item) + 1);} else {map.put(item, 1);}}}}for (char item : map.keySet()) {if (map.get(item) == 1) {isContinue = true;int i = numToRegion.get(item);board[i][j] = item;newBoard[i][j] = null;// 清除备选数字cleaNum(i, j, item+"", newBoard);}}}// 3*3单元格,一共9个for (int x = 0; x < 9; x++) {int row = (x/3)*3;int col = (x%3)*3;// 存储每个备选数字对应的坐标Map<Character, String> numToRegion = new HashMap<>();// 存储备选数字的个数Map<Character, Integer> map = new HashMap<>();for (int i = row; i < row+3; i++) {for (int j = col; j < col+3; j++) {if (newBoard[i][j] != null) {char[] chars = newBoard[i][j].toCharArray();for (char item : chars) {numToRegion.put(item, i + "," + j);if (map.containsKey(item)) {map.put(item, map.get(item) + 1);} else {map.put(item, 1);}}}}}for (char item : map.keySet()) {// 如果备选个数为1,那么就填入这个数字if (map.get(item) == 1) {String[] location = numToRegion.get(item).split(",");int i = Integer.parseInt(location[0]);int j = Integer.parseInt(location[1]);board[i][j] = item;newBoard[i][j] = null;isContinue = true;// 清除备选数字cleaNum(i, j, item+"", newBoard);}}}return isContinue;}/*** 暴力拆除法,依次尝试备选数字* @param board1 待解数独* @param newBoard1 剩余备选数字* @return 处理结果,返回 1 表示解数独完成,返回 2 表示没有解, 返回 3 表示备份数字错误,需要继续尝试下一个*/private int solveSudoku4(int startRow, int startCol, char[][] board1, String[][] newBoard1) {// 复制char[][] board = new char[9][9];String[][] newBoard = new String[9][9];for (int m = 0; m < 9; m++) {for (int n = 0; n < 9; n++) {board[m][n] = board1[m][n];newBoard[m][n] = newBoard1[m][n];}}// 随机选择一个备选数字for (int i = startRow; i < 9; i++) {for (int j = startCol; j < 9; j++) {if (StringUtils.isNotBlank(newBoard[i][j])) {int length = newBoard[i][j].length();for (int k = 0; k < length; k++) {char item = newBoard[i][j].charAt(k);board[i][j] = item;newBoard[i][j] = null;cleaNum(i, j, item+"", newBoard);boolean isContinue2 = true;while (isContinue2) {isContinue2 = solveSudoku2(board, newBoard) || solveSoduko3(board, newBoard);}int result = checkSodukoState(newBoard);if (1 == result) {// 复制最终结果for (int m = 0; m < 9; m++) {for (int n = 0; n < 9; n++) {board1[m][n] = board[m][n];newBoard1[m][n] = newBoard[m][n];}}return 1;} else if (2 == result) {int result2 = solveSudoku4(i, j, board, newBoard);if (1 == result2) {for (int m = 0; m < 9; m++) {for (int n = 0; n < 9; n++) {board1[m][n] = board[m][n];newBoard1[m][n] = newBoard[m][n];}}return 1;}}// 当最后一个备份数字也不符合时,需要修改前面一位备份数字if (k == length-1 && result == 3) {return 3;}// 回退到上一步,尝试下一个字符for (int m = 0; m < 9; m++) {for (int n = 0; n < 9; n++) {board[m][n] = board1[m][n];newBoard[m][n] = newBoard1[m][n];}}}}}}return 3;}/*** 判断数独状态* 1.newBoard值全为null, 表示全部解开* 2.newBoard里面有数字, 表示未完全解开* 3.newBoard里面没有数字,存在空字符串,表示数独不存在唯一解* @param newBoard 备选数字* @return 数独状态*/private int checkSodukoState(String[][] newBoard) {boolean isAllNull = true;for (int i=0; i<9; i++) {for (int j=0; j<9; j++) {if (newBoard[i][j] != null) {isAllNull = false;if ("".equals(newBoard[i][j])) {return 3;}}}}return isAllNull ? 1 : 2;}private final String[] ten = new String[]{"1","2","3","4","5","6","7","8","9"};private String getRestNum(String str) {String retStr = "";for (String item : ten) {if (!str.contains(item)) {retStr += item;}}return retStr;}private void printArr(char[][] chars) {System.out.println("===============================================================================");for (int i=0; i<9; i++) {for (int j=0; j<9; j++) {System.out.print(chars[i][j] + "\t");}System.out.println();}System.out.println("===============================================================================");}private void printStringArr(String[][] strs) {System.out.println("===============================================================================");for (int i=0; i<9; i++) {for (int j=0; j<9; j++) {System.out.print(strs[i][j] + "\t");}System.out.println();}System.out.println("===============================================================================");}@Testpublic void testLikou() {Set<Integer> temp = new HashSet<>();temp.add(1);temp.add(2);temp.remove(1);//temp.remove(2);long startTime = System.currentTimeMillis();int n=8;int k=8;if (k > n) {return;}if (k == 0) {return;}//combine4(n, k);//System.out.println(allCombineList.size());/*char[][] chars = new char[][]{{'.','.','9','7','4','8','.','.','.'},{'7','.','.','.','.','.','.','.','.'},{'.','2','.','1','.','9','.','.','.'},{'.','.','7','.','.','.','2','4','.'},{'.','6','4','.','1','.','5','9','.'},{'.','9','8','.','.','.','3','.','.'},{'.','.','.','8','.','3','.','2','.'},{'.','.','.','.','.','.','.','.','6'},{'.','.','.','2','7','5','9','.','.'}};*//*char[][] chars = new char[][]{{'5','.','2','.','6','.','.','.','.'},{'.','.','.','4','.','.','.','8','2'},{'.','.','.','.','.','2','.','.','1'},{'.','.','.','8','.','.','.','5','.'},{'.','.','3','.','.','.','6','.','.'},{'.','7','.','.','.','9','.','.','.'},{'8','.','.','2','.','.','.','.','.'},{'2','4','.','.','.','1','.','.','.'},{'.','.','.','.','3','.','2','.','7'}};*//*char[][] chars = new char[][]{{'.','.','8','.','.','.','2','.','.'},{'.','3','.','8','.','2','.','6','.'},{'7','.','.','.','9','.','.','.','5'},{'.','5','.','.','.','.','.','1','.'},{'.','.','4','.','.','.','6','.','.'},{'.','2','.','.','.','.','.','7','.'},{'4','.','.','.','8','.','.','.','6'},{'.','7','.','1','.','3','.','9','.'},{'.','.','1','.','.','.','8','.','.'}};*/// 专家级/*char[][] chars = new char[][]{{'8','.','6','.','5','.','3','.','.'},{'.','5','.','.','.','4','.','.','2'},{'4','.','.','.','.','.','.','1','.'},{'.','.','.','3','.','.','2','.','9'},{'7','.','5','.','.','.','.','.','.'},{'.','.','.','.','8','1','.','.','.'},{'.','.','8','2','.','.','9','.','.'},{'.','.','.','4','.','.','.','.','8'},{'.','2','.','.','6','3','.','.','.'},};*//*char[][] chars = new char[][]{{'6','.','.','.','.','.','5','.','.'},{'.','1','.','.','.','2','.','.','4'},{'.','.','7','.','3','.','.','6','.'},{'.','.','.','.','.','4','.','2','.'},{'.','.','.','.','6','1','.','.','.'},{'9','3','.','.','.','.','4','8','.'},{'.','8','.','7','1','.','.','9','.'},{'.','2','.','.','.','.','.','.','7'},{'7','.','.','.','5','.','.','.','.'},};*/// 世上最难数独char[][] chars = new char[][]{{'8','.','.','.','.','.','.','.','.'},{'.','.','3','6','.','.','.','.','.'},{'.','7','.','.','9','.','2','.','.'},{'.','5','.','.','.','7','.','.','.'},{'.','.','.','.','4','5','7','.','.'},{'.','.','.','1','.','.','.','3','.'},{'.','.','1','.','.','.','.','6','8'},{'.','.','8','5','.','.','.','1','.'},{'.','9','.','.','.','.','4','.','.'}};/*char[][] chars = new char[][]{{'.','.','.','.','5','.','.','3','.'},{'.','.','.','.','4','.','.','.','.'},{'.','9','.','.','.','.','.','.','2'},{'.','.','.','.','.','.','.','.','.'},{'6','.','.','.','.','.','.','4','.'},{'.','.','.','8','.','2','.','.','7'},{'5','.','.','.','.','.','.','.','.'},{'3','.','4','.','6','.','.','.','.'},{'.','.','.','7','.','.','2','.','9'}};*/solveSudoku(chars);printArr(chars);System.out.println("耗时: " + (System.currentTimeMillis() - startTime));}}

结果

在这里插入图片描述

  • 这边用了递归, 试了几个数独, 都能在1秒之内解开, 相比较而言, 数独只有九宫格, 所以暴力算法不算太耗时间.
  • 数独只知道这两个规则, 其他的没弄明白, 看百度百科上面介绍了一堆, 应该还能更快一点.
  • 暴力破解的速度很大程度上受到备选数字排序的影响.

参考

力扣解数独


http://chatgpt.dhexx.cn/article/8eBwC2e1.shtml

相关文章

力扣 37. 解数独

力扣 37. 解数独

一、题目描述 编写一个程序&#xff0c;通过填充空格来解决数独问题。 数独的解法需遵循如下规则&#xff1a; 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。数独部分空格内已填入了数字&#xf…
阅读更多...
LeetCode算法 —— 解数独

LeetCode算法 —— 解数独

题目如下所示&#xff1a; 编写一个程序&#xff0c;通过已填充的空格来解决数独问题。 一个数独的解法需遵循如下规则&#xff1a; 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。 空白格用 ‘.…
阅读更多...
C语言——解数独程序[源码]

C语言——解数独程序[源码]

用C语言写的解数独的程序。在linux下测试成功运行。 效果如图&#xff1a; 这是带解的数独&#xff0c;需要填写的部分用数字0代替。 这是程序运行后的效果图。看看&#xff0c;数独已经搞定啦&#xff5e;&#xff5e;&#xff5e; 程序源码如下&#xff1a; #include <…
阅读更多...
用 Python 解数独（Sudoku）

用 Python 解数独（Sudoku）

芬兰数学家因卡拉花费3个月时间设计出的世界上迄今难度最大的数独。数独是 9 横 9 竖共有 81 个格子&#xff0c;同时又分为 9 个九宫格。规则很简单&#xff1a;每个空格填入 1~9 任意一个数字&#xff0c;需要保证每个横排和竖排以及九宫格内无相同数字。 解数独是一个可有可…
阅读更多...
解数独c++

解数独c++

解数独 编写一个程序&#xff0c;通过填充空格来解决数独问题。 数独的解法需 遵循如下规则&#xff1a; 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。&#xff08;请参考示例图&#xff09; 数…
阅读更多...
MATLAB 解数独

MATLAB 解数独

数独是一种较为常见的游戏&#xff0c;一般有4乘4、6乘6、9乘9几种&#xff0c;就像下面这种&#xff0c;本文也是主要求解此类数独。 此外还有一些奇形怪状的&#xff0c;如下图两种&#xff0c;均是不规则的&#xff0c;在此并不会涉及&#xff0c;但会在以后发布代码以及过程…
阅读更多...
Leetcode 解数独

Leetcode 解数独

解数独 题目描述&#xff1a; 编写一个程序&#xff0c;通过填充空格来解决数独问题。一个数独的解法需遵循如下规则&#xff1a;数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。提示&#xff1a;…
阅读更多...
再战leetcode （解数独）

再战leetcode （解数独）

37. 解数独 题目描述 回溯法 leetcode题解 代码 public class Test {public static void main(String[] args) {char[][] board {{5, 3, ., ., 7, ., ., ., .},{6, ., ., 1, 9, 5, ., ., .},{., 9, 8, ., ., ., ., 6, .},{8, ., ., ., 6, ., ., ., 3},{4, ., ., 8, ., 3, .…
阅读更多...
回溯算法解数独问题（java版）

回溯算法解数独问题（java版）

下面来详细讲一下如何用回溯算法来解数独问题。 下图是一个数独题&#xff0c;也是号称世界上最难的数独。当然了&#xff0c;对于计算机程序来说&#xff0c;只要算法是对的&#xff0c;难不难就不知道了&#xff0c;反正计算机又不累。回溯算法基本上就是穷举&#xff0c;解这…
阅读更多...
014. 解数独

014. 解数独

1.题目链接&#xff1a; 37. 解数独 2.解题思路&#xff1a; 2.1.题目要求&#xff1a; 暂时的理解就是&#xff0c;编写一个程序然后自动填完数独&#xff0c;填完返回&#xff08;不用求解各种不同的数独组合&#xff09; 填的时候&#xff0c;数字要满足的规则&#xff1…
阅读更多...
回溯算法—解数独

回溯算法—解数独

什么是回溯法&#xff1f; 回溯法&#xff08;探索与回溯法&#xff09;是一种选优搜索法&#xff0c;又称为试探法&#xff0c;按选优条件向前搜索&#xff0c;以达到目标。但当探索到某一步时&#xff0c;发现原先选择并不优或达不到目标&#xff0c;就退回一步重新选择&…
阅读更多...
解数独--难的一批

解数独--难的一批

1题目 编写一个程序&#xff0c;通过填充空格来解决数独问题。 数独的解法需 遵循如下规则&#xff1a; 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。&#xff08;请参考示例图&#xff09; 数…
阅读更多...
解数独 — Python

解数独 — Python

文章目录 解数独1、程序简介示例&#xff1a;输入&#xff1a;输出&#xff1a;解释&#xff1a;提示&#xff1a; 2、程序代码3、运行结果 解数独 1、程序简介 编写一个程序&#xff0c;通过填充空格来解决数独问题。 数独的解法需 遵循如下规则&#xff1a; 数字 1-9 在每…
阅读更多...
【每日刷题】解数独

【每日刷题】解数独

题目地址 https://leetcode-cn.com/problems/sudoku-solver/ 题目描述&#xff1a;解数独 编写一个程序&#xff0c;通过已填充的空格来解决数独问题。 一个数独的解法需遵循如下规则&#xff1a; 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-…
阅读更多...
算法学习：37. 解数独

算法学习：37. 解数独

解数独 题目链接&#xff1a;力扣题目链接 难度&#xff1a;困难 编写一个程序&#xff0c;通过填充空格来解决数独问题。 数独的解法需 遵循如下规则&#xff1a; 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫…
阅读更多...
数独解题方法大全

数独解题方法大全

数独这个数字解谜游戏&#xff0c;完全不必要用到算术&#xff01;会用到的只是推理与逻辑。解题方法分两大类&#xff1a;直观法和候选数法。 直观法就是不需要任何辅助工具&#xff0c;从接到数独谜题的那一刻起就可以立即开始解题。绝不猜测。数独直观法解题技巧主要有&…
阅读更多...
37.解数独

37.解数独

37. 解数独&#xff08;难度&#xff1a;困难&#xff09; 题目链接&#xff1a;https://leetcode-cn.com/problems/sudoku-solver/ 编写一个程序&#xff0c;通过已填充的空格来解决数独问题。 一个数独的解法需遵循如下规则&#xff1a; 数字 1-9 在每一行只能出现一次。数…
阅读更多...
安装搜狗输入法成功，每次都折腾，记录一下这次的成功经验。

安装搜狗输入法成功，每次都折腾，记录一下这次的成功经验。

1&#xff1a;卸载fcitx sudo apt-get --purge fcitx* 2&#xff1a;清理系统内的无用的软件包 sudo apt-get --purge autoremove 3&#xff1a;到搜狗官网下载搜狗拼音输入法&#xff0c;选择你系统对应的软件包&#xff0c;我系统是64位的&#xff0c;所以我选择了amd64的 ht…
阅读更多...
Ubuntu16.04 python2.7升级python3.5

Ubuntu16.04 python2.7升级python3.5

原文地址&#xff1a;https://www.cnblogs.com/wmr95/p/7637077.html Ubuntu16.04 python2.7升级python3.5 正常情况下&#xff0c;你安装好ubuntu16.04版本之后&#xff0c;系统会自带 python2.7版本&#xff0c;如果需要下载新版本的python3.5&#xff0c;就需要进行更新。下…
阅读更多...
（转）解决Ubuntu2.6.31-20内核更新问题：Unable to mount root fs on unknown-block(x,x)

（转）解决Ubuntu2.6.31-20内核更新问题：Unable to mount root fs on unknown-block(x,x)

原文章&#xff1a;http://hi.baidu.com/%D2%BB%B5%E3%C7%E7/blog/item/d3b0df30da10a115ebc4afa3.html Ubuntu2.6.31-20内核更新问题&#xff1a;Unable to mount root fs on unknown-block(x,x) WUBI装的ubuntu。在更新了最信的内核 2.6.31-20&#xff0c;启动时出现提示&a…
阅读更多...
推荐文章

Copyright @ 2022~2023