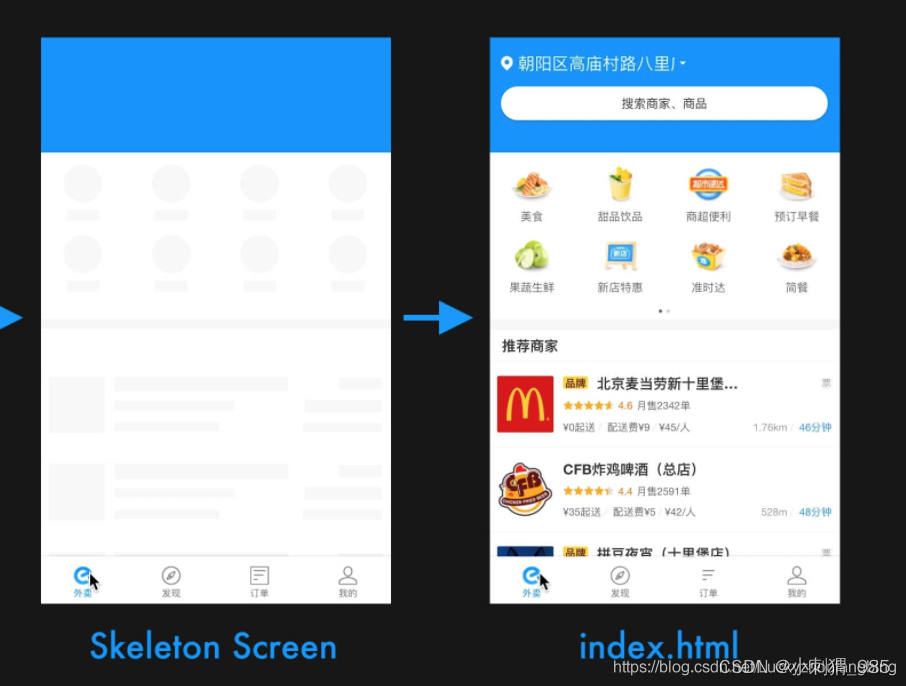
(一)什么是骨架屏
骨架屏可以理解为是当数据还未加载进来前,页面的一个空白版本。在页面完全渲染完成之前,用户会看到一个样式简单,描绘了当前页面的大致框架的页面,然后骨架屏中各个占位部分被实际资源完全替换,这个过程中用户会觉得内容正在逐渐加载即将呈现,降低了用户的焦躁情绪,使得加载过程主观上变得流畅。(先占位,内容逐渐呈现)
简单来说,骨架屏就是在页面内容未加载完成的时候,先使用一些图形进行占位,待内容加载完成之后再把它替换掉。
骨架屏会在感官上觉得内容出现的流畅而不突兀,体验更加优良。
(二)图片
(三)骨架屏用途
作为spa中路由切换的 loading, 结合组件的生命周期和ajax请求返回的时机来使用.( 作为loading 使用)。作为与用户联系最为密切的前端开发者,用户体验是最值得关注的问题。关于页面loading状态的展示,主流的主要有loading图和进度条两种。除此之外,越来越多的APP采用了“骨架屏”的方式去展示未加载内容,给予了用户焕然一新的体验。
作为首屏渲染的优化
(四)一个简单的骨架屏模拟
<!DOCTYPE html>
<html><head><meta charset="UTF-8" /><meta name="viewport" content="width=device-width, initial-scale=1.0" /><meta http-equiv="X-UA-Compatible" content="ie=edge" /><link href="https://cdn.bootcss.com/weui/2.1.2/style/weui.min.css" rel="stylesheet" /><title>Skeletons</title><style>img {width: 100%;}.media-box-img {width: 60px;height: 60px;}/* 阻止Skeletons点击事件 */.pointer-stop {pointer-events: none;}/* Skeletons效果 */.skeletons {position: relative;display: block;overflow: hidden;height: 100%;min-height: 20px;background-color: #ededed;}.skeletons:empty::after {display: block;content: '';position: absolute;width: 100%;height: 100%;-webkit-transform: translateX(-100%);transform: translateX(-100%);background: linear-gradient(90deg, transparent, rgba(216, 216, 216, 0.753), transparent);-webkit-animation: loading 1.5s infinite;animation: loading 1.5s infinite;}@-webkit-keyframes loading {100% {-webkit-transform: translateX(100%);transform: translateX(100%);}}@keyframes loading {100% {-webkit-transform: translateX(100%);transform: translateX(100%);}}</style></head><body><div class="weui-panel weui-panel_access"><div class="weui-panel__hd"><span class="weui-panel-title skeletons"></span></div><div class="weui-panel__bd"><a href="javascript:void(0);" class="weui-media-box weui-media-box_appmsg pointer-stop"><div class="weui-media-box__hd"><div class="media-box-img skeletons"></div></div><div class="weui-media-box__bd"><div class="weui-media-box__title skeletons"></div><p class="weui-media-box__desc"><span class="media-box-desc skeletons"></span></p></div></a></div></div><script>function renderCard() {var cardImage = document.querySelector('.weui-panel-title')cardImage.textContent = '标题'cardImage.classList.remove('skeletons')var listData = [{img:'data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAHgAAAB4CAMAAAAOusbgAAAAeFBMVEUAwAD///+U5ZTc9twOww7G8MYwzDCH4YcfyR9x23Hw+/DY9dhm2WZG0kbT9NP0/PTL8sux7LFe115T1VM+zz7i+OIXxhes6qxr2mvA8MCe6J6M4oz6/frr+us5zjn2/fa67rqB4IF13XWn6ad83nxa1loqyirn+eccHxx4AAAC/klEQVRo3u2W2ZKiQBBF8wpCNSCyLwri7v//4bRIFVXoTBBB+DAReV5sG6lTXDITiGEYhmEYhmEYhmEYhmEY5v9i5fsZGRx9PyGDne8f6K9cfd+mKXe1yNG/0CcqYE86AkBMBh66f20deBc7wA/1WFiTwvSEpBMA2JJOBsSLxe/4QEEaJRrASP8EVF8Q74GbmevKg0saa0B8QbwBdjRyADYxIhqxAZ++IKYtciPXLQVG+imw+oo4Bu56rjEJ4GYsvPmKOAB+xlz7L5aevqUXuePWVhvWJ4eWiwUQ67mK51qPj4dFDMlRLBZTqF3SDvmr4BwtkECu5gHWPkmDfQh02WLxXuvbvC8ku8F57GsI5e0CmUwLz1kq3kD17R1In5816rGvQ5VMk5FEtIiWislTffuDpl/k/PzscdQsv8r9qWq4LRWX6tQYtTxvI3XyrwdyQxChXioOngH3dLgOFjk0all56XRi/wDFQrGQU3Os5t0wJu1GNtNKHdPqYaGYQuRDfbfDf26AGLYSyGS3ZAK4S8XuoAlxGSdYMKwqZKM9XJMtyqXi7HX/CiAZS6d8bSVUz5J36mEMFDTlAFQzxOT1dzLRljjB6+++ejFqka+mXIe6F59mw22OuOw1F4T6lg/9VjL1rLDoI9Xzl1MSYDNHnPQnt3D1EE7PrXjye/3pVpr1Z45hMUdcACc5NVQI0bOdS1WA0wuz73e7/5TNqBPhQXPEFGJNV2zNqWI7QKBd2Gn6AiBko02zuAOXeWIXjV0jNqdKegaE/kJQ6Bfs4aju04lMLkA2T5wBSYPKDGF3RKhFYEa6A1L1LG2yacmsaZ6YPOSAMKNsO+N5dNTfkc5Aqe26uxHpx7ZirvgCwJpWq/lmX1hA7LyabQ34tt5RiJKXSwQ+0KU0V5xg+hZrd4Bn1n4EID+WkQdgLfRNtvil9SPfwy+WQ7PFBWQz6dGWZBLkeJFXZGCfLUjCgGgqXo5TuSu3cugdcTv/HjqnBTEMwzAMwzAMwzAMwzAMw/zf/AFbXiOA6frlMAAAAABJRU5ErkJggg==',desc: '内容内容内容内容'}]var html = ''var cardImage1 = document.querySelectorAll('.media-box-img')var cardImage2 = document.querySelectorAll('.weui-media-box')var cardImage3 = document.querySelectorAll('.weui-media-box__title')var cardImage4 = document.querySelectorAll('.media-box-desc')for (var i = 0; i < listData.length; i++) {cardImage2[i].classList.remove('pointer-stop')cardImage1[i].classList.remove('skeletons')cardImage3[i].classList.remove('skeletons')cardImage4[i].classList.remove('skeletons')cardImage1[i].innerHTML = "<img src='" + listData[i].img + "' />"cardImage3[i].innerHTML = '一段标题'cardImage4[i].innerHTML = '一段描述'}}setTimeout(function() {renderCard()}, 4000)</script></body>
</html>