内容来自《计算机图形学》第四版 第14章-样条表示

---

---

• 样条：通过一组指定点集生成平滑曲线的柔型带
• 样条曲线：计算机图形学中，样条曲线指多项式曲线段连接而成的曲线

[1] 样条的种类

给定一组控制点，可以生成一条样条曲线，这些点给出了曲线的大致形状。根据这些控制点位置，可以使用以下两种方法之一选取分段连续参数多项式函数。

1. 插值样条

当选取的多项式使得曲线通过每个控制点，则所得曲线称为该组控制点的插值（interpolate）样条曲线。插值曲线常用于数字化绘图或指定路径。

方法包括：

• 自然三次样条
• Hermite 插值
• Cardinal 样条
• Kochanek-Bartels 样条

2. 逼近样条

另一情况，当选取的多项式使部分或全部控制点不在生成的曲线上，则所得曲线称为该组控制点的逼近（approximate）样条曲线。逼近曲线一般作为设计工具来构造对象形体。

方法包括

• Bezier曲线
• B样条
• Beta样条
• 有理样条

[2] 参数连续性条件

为保证分段参数曲线从一段到另一段连续过渡，可以在连接点处要求各种连续性条件（continuity conditions），如样条的每一部分以参数方程描述：

$x=x(u),y=y(u),z=z(u),u\in [u_1,u_2]$

则通过曲线段公共部分匹配连接的参数导数，从而建立参数连续性（parametric continuity）。

0阶参数连续性 $C^0$ 简单地表示曲线相连；

一阶参数连续性 $C^1$ 说明代表两条相邻曲线段的方程在相交点处有相同的一阶导数：如连接点$u_0$两侧曲线的参数方程分别为$x_1(u),y_1(u)$和$x_2(u),y_2(u)$，那么$x_1^{\prime }(u)=x_2^{\prime }(u)$且$y_1^{\prime }(u)=y_2^{\prime }(u)$时达到一阶参数连续性，其中’表示对参数$u$求导。

二阶参数连续性 $C^2$ 同理，表示交点处切向量的变化率相等。

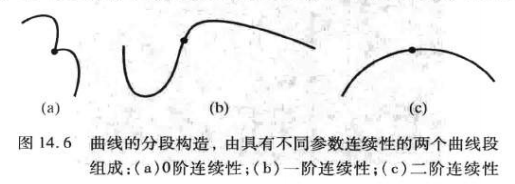
[2] 几何连续性条件

0阶几何连续性 $G^0$ 和一阶参数连续性$C^0$含义相同，表示曲线相连；

一阶几何连续性 $G^1$ 说明代表两条相邻曲线段的方程在相交点处的参数导数成比例：如连接点$u_0$两侧曲线的参数方程分别为$x_1(u),y_1(u)$和$x_2(u),y_2(u)$，那么$x_1^{\prime }(u)/y_1^{\prime }(u)=x_2^{\prime }(u)/y_2^{\prime }(u)$时达到一阶几何连续性，其中’表示对参数$u$求导。实际上，即不用参数表达曲线时，曲线写成$y=f(x)$，交点两侧曲线y对x导数相等。

二阶几何连续性 $G^2$ 同理。

[3] 样条描述

以三次样条为例，有以下三种等价描述：

1. 列出一组施加在样条上的边界条件

列出参数表达式，以x为例：

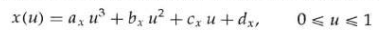
曲线的边界条件可以设为端点坐标$x(0)$和$x(1)$及端点处的一次导数$x^{\prime }(0)$和$x^{\prime }(1)$，这四个边界条件即可充分确定四个系数。

2. 列出描述样条特征的行列式

将上述参数方程重写为矩阵型

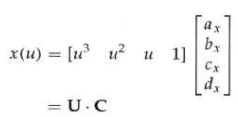
U是参数u的幂次行矩阵，C是系数列矩阵。C可通过边界条件解方程求得：

$M_{geom}$是包含样条上几何约束值（边界条件，包括控制点坐标值和其他已指定的几何约束）的四元素列矩阵，$M_{spline}$将几何约束值转化称多项式系数。从而可以得到

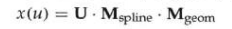
$M_{spline}$描述了一个样条表示，称为基本矩阵。

3. 列出一组混合函数或基函数

最后，通过特征方程，可以得到关于坐标x的几何约束参数多项式表示：

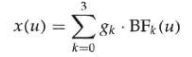
$g_k$是约束参数，类似控制点坐标和控制点处的曲线斜率，$B{F}_k$是混合函数或称为基函数。

[4] 三次样条插值方法

1. 自然三次样条 Natural Cubic Spline

在使用公式表示一个自然三次样条时，需要两个相邻曲线段正在公共边界处有相同的一阶和二阶导数，即自然三次样条具有$C^2$连续性。

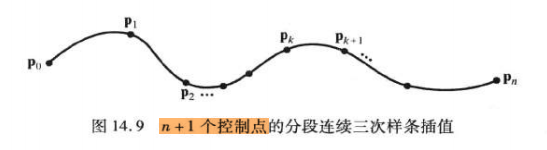
如图，以参数方程$x(u)$为例，有n+1个控制点，n段曲线，每段曲线4个系数，共有4n个多项式系数待定。

分析约束数量：除去首末控制点，共n-1个内部控制点，每个内部控制点需要满足四个约束，包括左右两端曲线经过该控制点、左右两端对参数一阶导数和二阶导数相等。这样出现4n-4个约束。 对于首末控制点，各有一个位置约束，则共有4n-2个约束。还需两个约束条件，这时有两种解决方案：

• 指定首末控制点处二阶导数=0
• 增加两个隐含控制点，分别位于原首末控制点的外侧。这时，所有控制点都成为内部控制点，即满足4n个约束条件。

自然三次样条的主要缺陷： 若控制点中的任意一个发生了变动，则整条曲线都要受到影响，即不支持“局部控制”。

2. Hermite 插值

指定每个曲线段的控制点的位置和一阶导数，那么对每个内部控制点，有4个约束：两侧曲线经过该控制点、两侧曲线导数等于给定值；对于首末控制点，各有2个约束，分别是位置约束和导数约束。那么共计4(n-1)+2*2 = 4n个约束。

这样，Hermite样条支持局部调整，因为每个曲线段仅依赖其端点的约束。

记每一段曲线的约束为端点$p_k,p_{k+1}$和端点斜率$D{p}_k,D{p}_{k+1}$，则参考[3]-2，可以通过约束计算系数，带入曲线表达式可得：

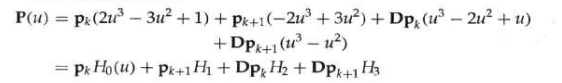
实际上，在这里，H即为基函数，也成为混合函数。

但是，除了控制点坐标之外，更好的处理方法是不需要处理输入曲线的斜率或其它几何信息即能生成样条曲线，Cardinal 样条和Kochanek-Bartels 样条可以满足这样的要求。

3. Cardinal 样条

在Cardinal样条中，一个控制点的一阶导数值可以由两个相邻控制点的坐标进行计算。

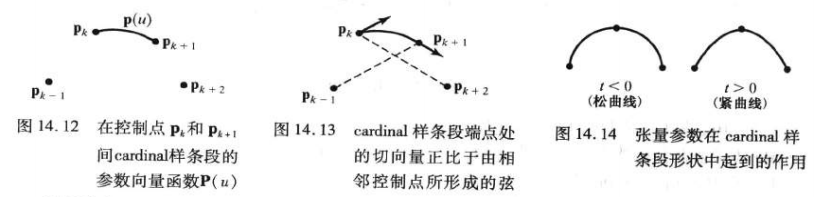
一个Cardinal样条完全由四个连续控制点给出，中间两个控制点是曲线端点，另外两个点用于计算端点斜率。

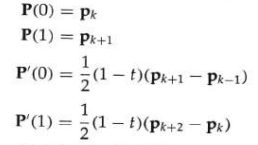
控制点$p_k$和$p_{k+1}$处的一阶导数和弦$p_{k-1}{p}_{k+1}$、$p_k{p}_{k+2}$成正比。参数t称为张量（tension）参数，控制样条与输入控制点之间的松紧程度。当t=0时，这样的曲线称为Catmull-Rom样条或Overhauser样条。

4. Kochanek-Bartels 样条

Kochanek-Bartels 样条是Cardinal样条的扩展，将两个附加参数引入到约束方程中，从而为调整曲线形状提供更多方便。

t是张量参数，b是偏离参数，c为连续性参数。

即通过其他控制点控制某控制点的导数的方式更复杂一些，可以产生更多控制效果。