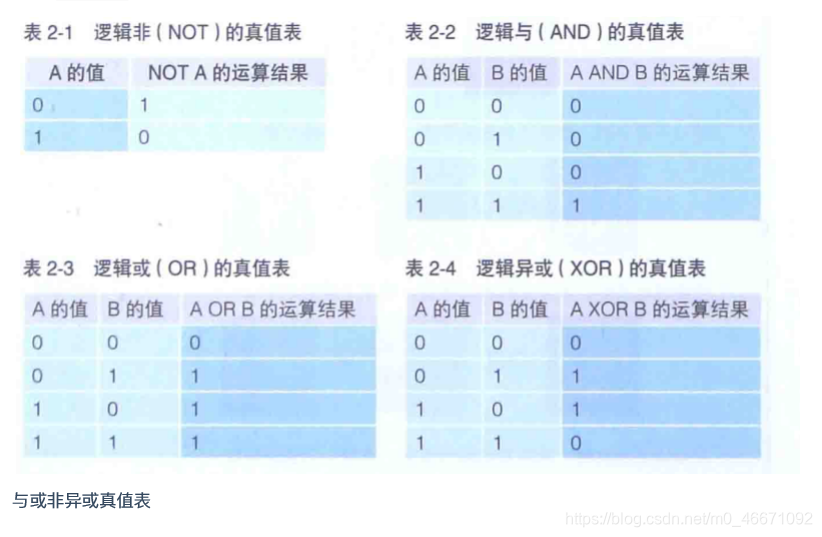
需求
近期在做公司上位机产品规划与实验,参考了Blender软件的布局风格,希望能用WPF也做一个类似布局的上位机。于是开始寻找资源,很快就发现了AvalonDock。
AvalonDock简介
AvalonDock是Xceed公司 Wpf.Toolkit 中的一款收费产品,其中还包括很多其他控件的收集整理,感兴趣的自行研究。
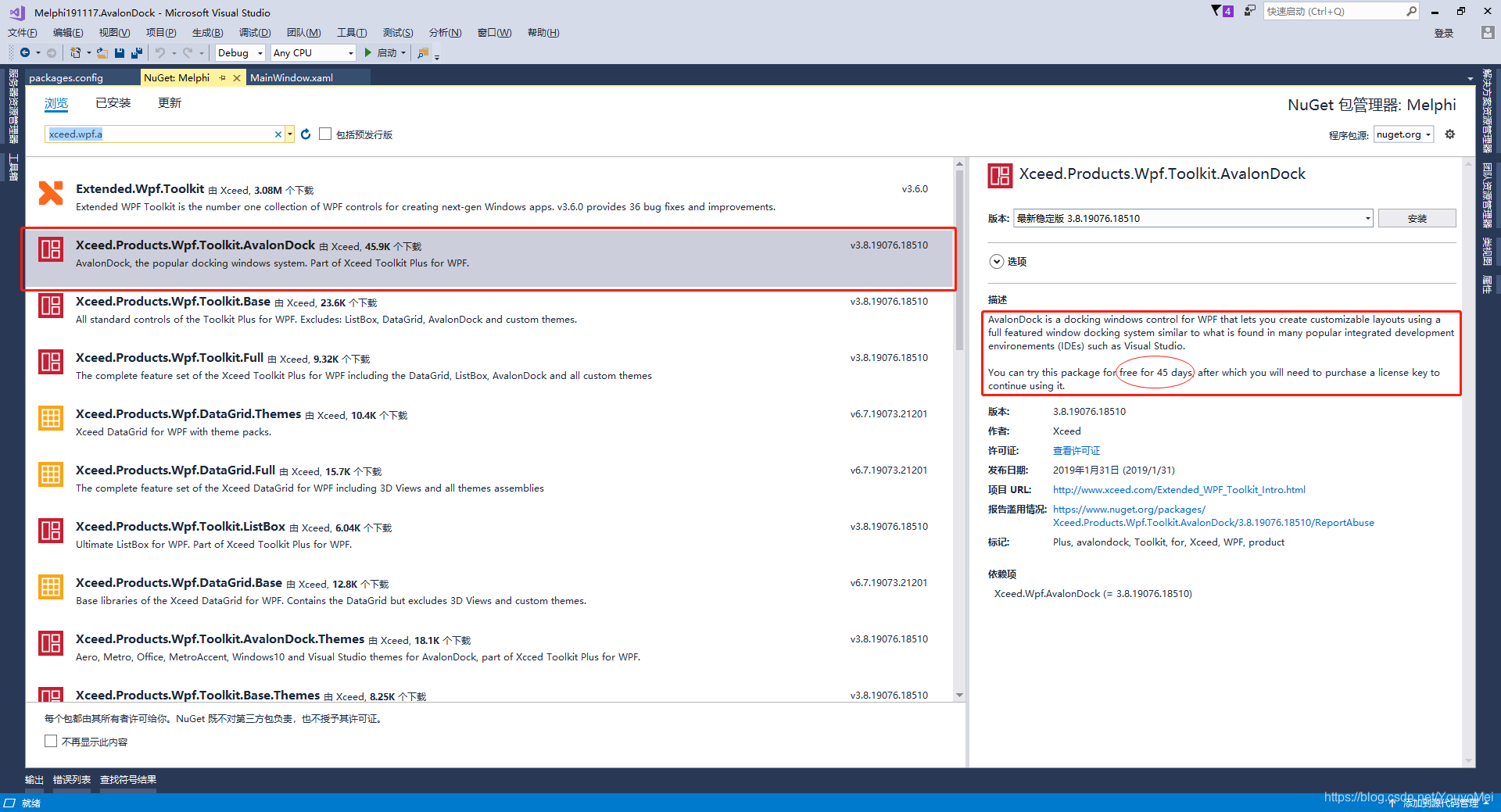
但是万能的Nuget里面有许多免费的版本,并且GitHub开源。下面就给列举一个自己使用的Dirkster.AvalonDock。
使用
1.创建我们自己的WPF项目
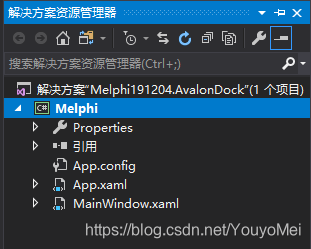
2.使用NuGet引入Dirkster.AvalonDock资源库
步骤:右键项目(Melphi)-->管理NuGet程序包-->浏览-->输入"Dirkster.AvalonDock"-->选择"Dirkster.AvalonDock"点击安装即可
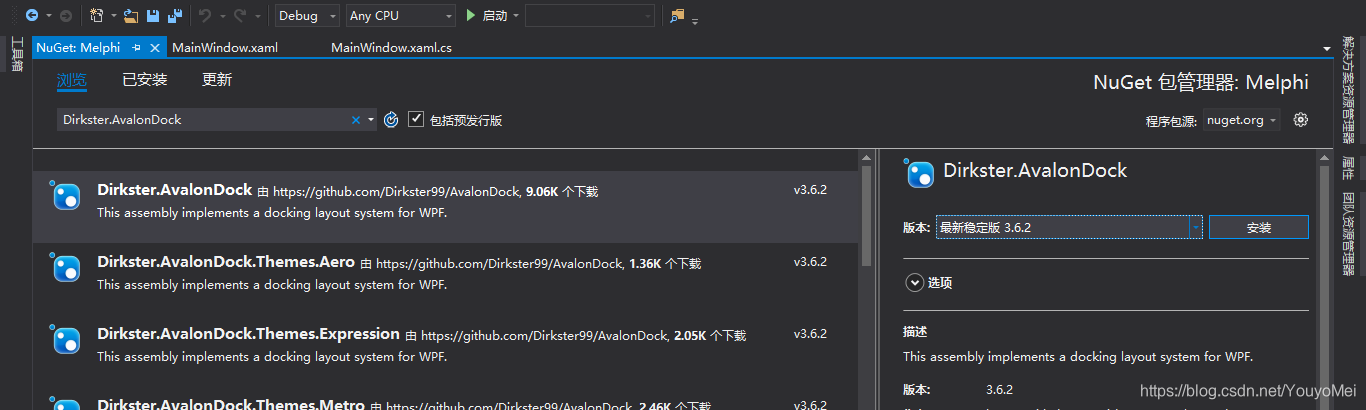
3.使用
这里只是为了演示效果,我就直接把代码贴出来了,不做解释。控件如何使用,请查看其源码:https://github.com/Dirkster99/AvalonDock或者其他博主。
<Window x:Class="Melphi.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d="http://schemas.microsoft.com/expression/blend/2008"xmlns:mc="http://schemas.openxmlformats.org/markup-compatibility/2006"xmlns:local="clr-namespace:Melphi"xmlns:avalon="http://schemas.xceed.com/wpf/xaml/avalondock"mc:Ignorable="d"Title="MainWindow" Height="450" Width="800"><Grid><Grid.RowDefinitions><RowDefinition Height="Auto"/><RowDefinition Height="*"/><RowDefinition Height="Auto"/></Grid.RowDefinitions><Menu><MenuItem Header="File"><MenuItem Header="New"/><MenuItem Header="Open"/></MenuItem><MenuItem Header="Edit"><MenuItem Header="Undo"/><MenuItem Header="Cut"/><MenuItem Header="Copy"/></MenuItem><MenuItem Header="View"><MenuItem Header="Explorer"/><MenuItem Header="Open"/></MenuItem><MenuItem Header="Tool"><MenuItem Header="Extentions"/><MenuItem Header="Options"/></MenuItem><MenuItem Header="Help"><MenuItem Header="Welcome"/><MenuItem Header="Support"/><MenuItem Header="About"/></MenuItem></Menu><avalon:DockingManager Grid.Row="1"><avalon:DockingManager.Theme><avalon:GenericTheme></avalon:GenericTheme></avalon:DockingManager.Theme><avalon:LayoutRoot><avalon:LayoutPanel Orientation="Horizontal"><avalon:LayoutAnchorablePaneGroup DockWidth="150" FloatingWidth="240"><avalon:LayoutAnchorablePane x:Name="panelLeft"><avalon:LayoutAnchorable Title="Tool"></avalon:LayoutAnchorable><avalon:LayoutAnchorable Title="Team"></avalon:LayoutAnchorable></avalon:LayoutAnchorablePane></avalon:LayoutAnchorablePaneGroup><avalon:LayoutPanel Orientation="Vertical"><avalon:LayoutDocumentPaneGroup><avalon:LayoutDocumentPane x:Name="panelTop"><avalon:LayoutDocument Title="MainWindow.xaml"></avalon:LayoutDocument><avalon:LayoutDocument Title="MainWindow.xaml.cs"></avalon:LayoutDocument></avalon:LayoutDocumentPane></avalon:LayoutDocumentPaneGroup><avalon:LayoutAnchorablePaneGroup DockMinHeight="30" DockHeight="100" FloatingHeight="180"><avalon:LayoutAnchorablePane x:Name="panelBottom"><avalon:LayoutAnchorable Title="Output"></avalon:LayoutAnchorable><avalon:LayoutAnchorable Title="Exception"></avalon:LayoutAnchorable><avalon:LayoutAnchorable Title="Error"></avalon:LayoutAnchorable></avalon:LayoutAnchorablePane></avalon:LayoutAnchorablePaneGroup></avalon:LayoutPanel><avalon:LayoutAnchorablePaneGroup DockMinWidth="50" DockWidth="150" FloatingWidth="270"><avalon:LayoutAnchorablePane x:Name="panelRight" DockWidth="240" FloatingWidth="240"><avalon:LayoutAnchorable Title="Solution"></avalon:LayoutAnchorable><avalon:LayoutAnchorable Title="Property"></avalon:LayoutAnchorable></avalon:LayoutAnchorablePane></avalon:LayoutAnchorablePaneGroup></avalon:LayoutPanel></avalon:LayoutRoot></avalon:DockingManager><Border Grid.Row="2" Background="AliceBlue" Height="20"></Border></Grid>
</Window>
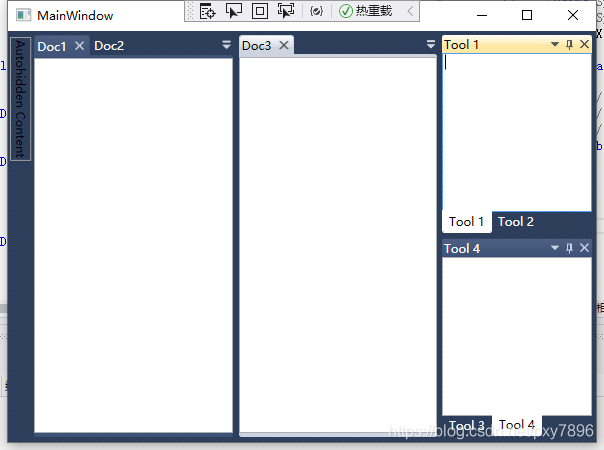
4.效果
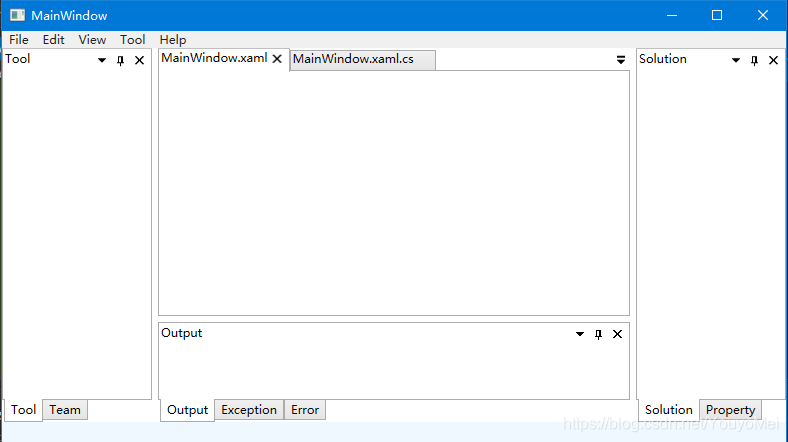
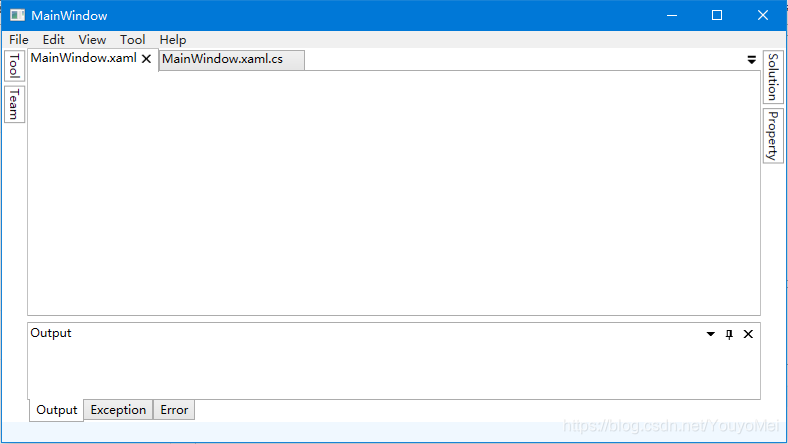
总结
学会查找资料,那将是你尽快抵达下一站的不二捷径。
Over
每次记录一小步...点点滴滴人生路...