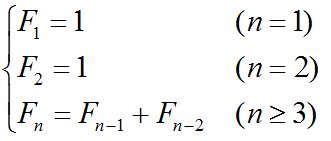一、什么是Fibonacci数列

• 斐波那契数列指的是这样一个数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
• 用文字来说，就是从第3项开始，每一项都等于前两项之和。
• 至于包不包括0，一番查阅后没有得到证实… 不过重要的是“第3项开始，每一项都等于前两项之和”这个定义。

二、简单递归

1. 设计递归方程

• 斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
• 递归定义：
  $$F(n)=\{\begin{array}{ll}1& n=1\\ 1& n=2\\ F(n-1)+F(n-2)& n>2\end{array}$$
• 当 n=1 || n=2 时，结束递归。

2. 编写程序代码

// 【递归】Fibonacci数列（斐波那契数列）
#include<iostream>
using namespace std;int fibonacci(int num);int main()
{int num = 0; // 项数cout << "Fibonacci数列，请输入项数（正整数）：";cin >> num;cout << "此项为：" << fibonacci(num) << endl;	//输出结果return 0;
}int fibonacci(int num)
{if (num <= 2)return 1;		// F(1)=1，F(2)=1elsereturn fibonacci(num - 1) + fibonacci(num - 2);	// F(n)=F(n-1)+F(n-2)
}

3. 运行结果

三、动态规划

1. 再次分析上述递归算法

• 我们举例研究一下上面的递归算法：计算F(5)

    F(5) = F(4) + F(3);-> F(4) = F(3) + F(2);-> F(3) = F(2) + F(1);-> F(2) = 1;-> F(1) = 1;-> F(3) = F(2) + F(1); // 重复计算了 F(3)-> F(2) = 1;-> F(1) = 1;

• 从F(5)的例子中可以明显看到在递归中F(3)被我们重复计算了；
  少次循环中这并不明显，但可以想象，当递归层数非常大时，我们将会进行非常大量的重复计算，浪费大量的时间和资源。
• 我们很容易想到：既然重复计算了，那我们把计算过的值保存一下就好了嘛。

2. 动态规划

• 动态规划的基本思想是：将原问题拆分为若干子问题，自底向上的求解。
• 是自底向上的求解，即是先计算子问题的解，再得出原问题的解。动态规划详情–>详情

3. 备忘录法

• 备忘录法是自顶向下的算法，控制结构与直接递归相似，但其维护了一个记录子问题的表，以此避免了子问题的重复求解。

4. 程序实现

（1）动态规划 - 自底向上

// 【动态规划】Fibonacci数列（斐波那契数列）
#include<iostream>
using namespace std;int main()
{// 项数int n;cout << "Fibonacci数列，请输入项数：";cin >> n;// 保存计算过的值int* F = new int[n];F[1] = 1; // F(1)=1F[2] = 1; // F(2)=1// 自底向上计算for (int i = 3;i < n;i++)F[i] = F[i - 1] + F[i - 2];// 输出结果cout << F[n] << endl;delete[] F;return 0;
}

（2）备忘录法 - 自顶向下

// 【备忘录法】Fibonacci数列（斐波那契数列）
#include<iostream>
using namespace std;int F[256] = { 0 };	// 保存子问题解的表int fibonacci(int n);int main()
{// 项数int n;cout << "Fibonacci数列，请输入项数（正整数）：";cin >> n;// 保存子问题解的表，前两个数为 1F[1] = 1;F[2] = 1;// 自顶向下计算，并保存子问题的解；输出结果cout << fibonacci(n) << endl;return 0;
}int fibonacci(int n)
{if (F[n] > 0)return F[n];elsereturn (F[n] = fibonacci(n - 1) + fibonacci(n - 2));
}

• 运行结果都一样，如上图。

三、友情链接~

• 其它一些常见算法请参阅此链接~

---

最后，非常欢迎大家来讨论指正哦！