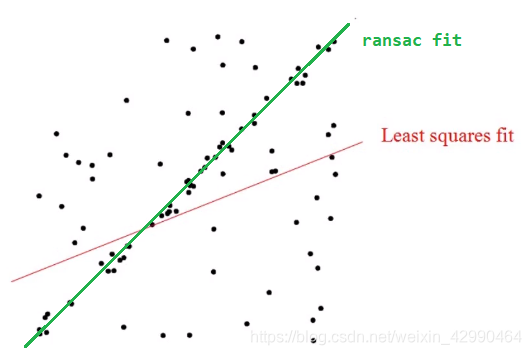
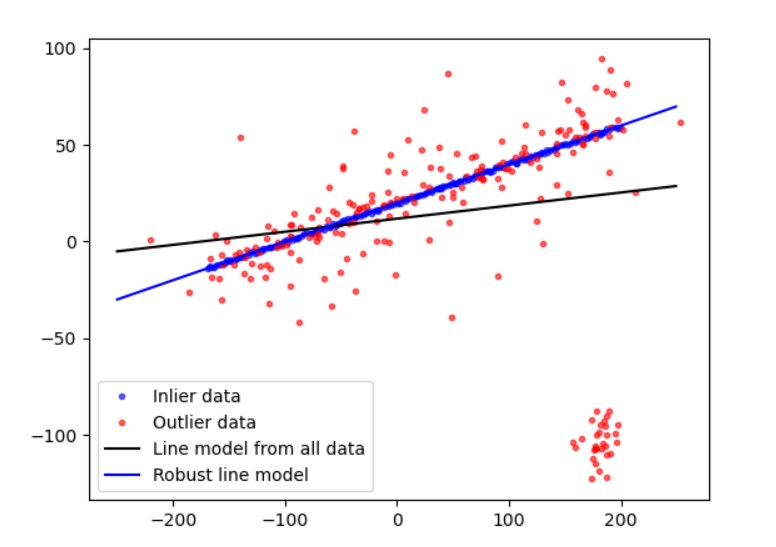
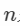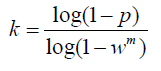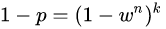一、RANSAC算法
1.参考资料
[1]题目来源与解析:商汤科技SLAM算法岗的RANSAC编程题
[2]牛客网题目:[编程题]线性回归
[3]牛客网解答参考:商汤科技某算法岗的编程题有点过分了啊
[4]RANSAC算法原理:RANSAC翻译、经典RANSAC以及其相关的改进的算法小结
[5]参考代码(只进行两点的估计):RANSAC 直线拟合算法
[6]最小二乘拟合直线原理:最小二乘法直线拟合:Ax+By+C=0
[7]最小二乘拟合直线代码:Ax+By+C=0 直线一般式拟合 c++/python
[8]最小二乘原理推导:最小二乘法求回归直线方程的推导过程
2.题目要求
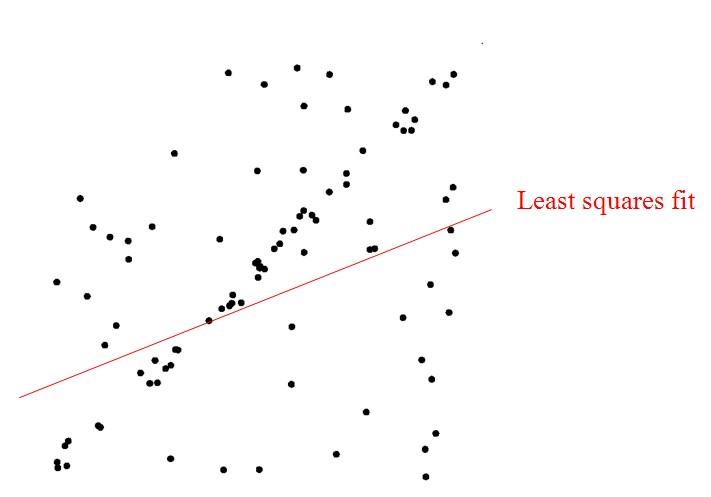
拟合二维平面中的带噪音直线,
其中有不超过10%的样本点远离了直线,另外90%的样本点可能有高斯噪声的偏移
要求输出为
ax+by+c=0的形式
其中a > 0 且 a^2 + b^2 = 1
输入描述:
第一个数n表示有多少个样本点 之后n*2个数 每次是每个点的x 和y
输出描述:
输出a,b,c三个数,至多可以到6位有效数字
示例1
输入
5
3 4
6 8
9 12
15 20
10 -10
输出
-0.800000 0.600000 0.000000
说明
本题共有10个测试点,每个点会根据选手输出的参数计算非噪音数据点的拟合误差E,并根据E来对每个数据点进行评分0-10分
输入数据的范围在-10000
3.RANSAC算法伪代码(转自[4])
伪码形式的算法如下所示:
输入:
data —— 一组观测数据
model —— 适应于数据的模型
n —— 适用于模型的最少数据个数
k —— 算法的迭代次数
t —— 用于决定数据是否适应于模型的阀值
d —— 判定模型是否适用于数据集的数据数目
输出:
best_model —— 跟数据最匹配的模型参数(如果没有找到好的模型,返回null)
best_consensus_set —— 估计出模型的数据点
best_error —— 跟数据相关的估计出的模型错误
iterations = 0
best_model = null
best_consensus_set = null
best_error = 无穷大
while ( iterations < k )maybe_inliers = 从数据集中随机选择n个点maybe_model = 适合于maybe_inliers的模型参数consensus_set = maybe_inliersfor ( 每个数据集中不属于maybe_inliers的点 )if ( 如果点适合于maybe_model,且错误小于t )将点添加到consensus_setif ( consensus_set中的元素数目大于d )已经找到了好的模型,现在测试该模型到底有多好better_model = 适合于consensus_set中所有点的模型参数this_error = better_model究竟如何适合这些点的度量if ( this_error < best_error )我们发现了比以前好的模型,保存该模型直到更好的模型出现best_model = better_modelbest_consensus_set = consensus_setbest_error = this_error增加迭代次数
返回 best_model, best_consensus_set, best_error3.最小二乘求解直线
公共内容:
| 变量名 | 计算公式 |
| mX | |
| mY | |
| sXX | |
| sXY | |
| sYY |
解法1:
参考资料[6]
解法2:
拟合直线 :
最小化点到直线的平方和:
函数f对参数a求导,并令其为0
求得
将上式带入f,对参数b求导,并令其为0,有
或者f对参数b求导后,将带入方程有
本文采用第一种形式
注意,采用同样的参数
int k = 50; //最大迭代次数
int n = 2; //适用于模型的最少数据个数
double t = 0.01; //用于决定数据是否适应于模型的阀值
int d = data_size*0.5; //判定模型是否适用于数据集的数据数目
解法1的通过率为100%
解法2的通过率为77.78%
暂时不明白为什么……
解法3:
根据参考资料[6],转换为二次型求最小值问题
第一种方法使用特征值分解,选取最小特征值对应的特征向量
第二种方法在二次型中,使用替换待求量,求解参数方程
后续有时间的话会补上程序
4.算法实现
可以通过自定义模型,将该代码移植到其他程序中
/*************************************************
Author: SayheyheyheyDate:2019-7-4Description:根据伪代码实现通用的RANSAC模板自定义线性模型,实现两种方式的直线拟合
**************************************************/#include <random>
#include <iostream>
#include <time.h>
#include <set>
#include <cassert>
#include <limits.h>using namespace std;
//数据点类型
struct st_point{st_point(){};st_point(double X, double Y) :x(X), y(Y){};double x;double y;
};
/*** @brief 线性模型** Ax+By+C = 0;
*/
class linearModel{
public://待估计参数double A, B, C;
public:linearModel(){};~linearModel(){};//使用两个点对直线进行初始估计void Update(vector<st_point> &data, set<int> &maybe_inliers){assert(maybe_inliers.size() == 2); //初始化的点不为2个,报错//根据索引读取数据vector<int> points(maybe_inliers.begin(), maybe_inliers.end());st_point pts1 = data[points[0]];st_point pts2 = data[points[1]];//根据两个点计算直线参数(得到其中一组解,可以任意比例缩放)double delta_x = pts2.x - pts1.x;double delta_y = pts2.y - pts1.y;A = delta_y;B = -delta_x;C = -delta_y*pts2.x + delta_x*pts2.y;}//返回点到直线的距离double computeError(st_point point){double numerator = abs(A*point.x + B*point.y + C);double denominator = sqrt(A*A + B*B);return numerator / denominator;}//根据一致点的集合对直线进行重新估计double Estimate(vector<st_point> &data, set<int> &consensus_set){assert(consensus_set.size() >= 2);//求均值 meansdouble mX, mY;mX = mY = 0;for (auto &index : consensus_set){mX += data[index].x;mY += data[index].y;}mX /= consensus_set.size();mY /= consensus_set.size();//求二次项的和 sumdouble sXX, sYY, sXY;sXX = sYY = sXY = 0;for (auto &index : consensus_set){st_point point;point = data[index];sXX += (point.x - mX)*(point.x - mX);sYY += (point.y - mY)*(point.y - mY);sXY += (point.x - mX)*(point.y - mY);}/*//解法1:求y=kx+b的最小二乘估计,然后再转换成一般形式//参考 https://blog.csdn.net/hookie1990/article/details/91406309bool isVertical = sXY == 0 && sXX < sYY;bool isHorizontal = sXY == 0 && sXX > sYY;bool isIndeterminate = sXY == 0 && sXX == sYY;double k = NAN;double b = NAN;if (isVertical){A = 1;B = 0;C = mX;}else if (isHorizontal){A = 0;B = 1;C = mY;}else if (isIndeterminate){A = NAN;B = NAN;C = NAN;}else{k = (sYY - sXX + sqrt((sYY - sXX) * (sYY - sXX) + 4.0 * sXY * sXY)) / (2.0 * sXY); //斜率b = mY - k * mX; //截距//正则化项,使得A^2+B^2 = 1;double normFactor = 1 / sqrt(1 + k*k);A = normFactor * k;B = -normFactor;C = normFactor*b;}//返回残差if (isIndeterminate){return NAN;}double error = A*A*sXX + 2 * A*B*sXY + B*B*sYY;error /= consensus_set.size();return error;*///解法2:if(sXX == 0){A = 1; B = 0;C = -mX;}else{A = sXY/sXX;B = -1;C = mY - A*mX;//归一化令A^2+B^2 = 1;double normFactor = sqrt(A*A+B*B);A /= normFactor;B /= normFactor;C /= normFactor;}double error = A*A*sXX + 2 * A*B*sXY + B*B*sYY;error /= consensus_set.size(); //求平均误差return error;}
};/**
* @brief 运行RANSAC算法
*
* @param[in] data 一组观测数据
* @param[in] n 适用于模型的最少数据个数
* @param[in] k 算法的迭代次数
* @param[in] t 用于决定数据是否适应于模型的阀值
* @param[in] d 判定模型是否适用于数据集的数据数目
* @param[in&out] model 自定义的待估计模型,为该函数提供Update、computeError和Estimate三个成员函数
* 运行结束后,模型参数被设置为最佳的估计值
* @param[out] best_consensus_set 输出一致点的索引值
* @param[out] best_error 输出最小损失函数
*/
template<typename T, typename U>
int ransac(vector<T> &data, int n, int k, double t, int d,U &best_model,set<int> &best_consensus_set, double &best_error){//1.初始化int iterations = 0; //迭代次数U maybe_model; //使用随机选点初始化求得的模型U better_model; //根据符合条件的一致点拟合出的模型int isFound = 0; //算法成功的标志set<int> maybe_inliers; //初始随机选取的点(的索引值)//best_error = DBL_MAX; //初始化为最大值best_error = 1.7976931348623158e+308;default_random_engine rng(time(NULL)); //随机数生成器uniform_int_distribution<int> dist(0, data.size()-1); //采用均匀分布//2.主循环while (iterations < k){//3.随机选点maybe_inliers.clear(); while (1){int index = dist(rng);maybe_inliers.insert(index);if (maybe_inliers.size() == n){break;}}//4.计算初始值maybe_model.Update(data, maybe_inliers); //自定义函数,更新模型set<int> consensus_set(maybe_inliers.begin(),maybe_inliers.end()); //选取模型后,根据误差阈值t选取的内点(的索引值)//5.根据初始模型和阈值t选择内点 for (int i = 0; i < data.size(); i++){double error_per_item = maybe_model.computeError(data[i]);if (error_per_item < t){consensus_set.insert(i);}}//6.根据全部的内点重新计算模型if (consensus_set.size() > d){double this_error = better_model.Estimate(data, consensus_set); //自定义函数,(最小二乘)更新模型,返回计算出的误差//7.若当前模型更好,则更新输出量if (this_error < best_error){best_model = better_model;best_consensus_set = consensus_set;best_error = this_error;}isFound = 1;}++iterations;}return isFound;
}int main(){//1.读入数据int data_size; //输入第一行表示数据大小cin >> data_size; vector<st_point> Points(data_size);for (int i = 0; i < data_size; i++){cin >> Points[i].x >> Points[i].y;}//测试用//vector<st_point> Points{ st_point(3, 4), st_point(6, 8), st_point(9, 12), st_point(15, 20), st_point(10,-10)};//int data_size = Points.size();//2.设置输入量int k = 50; //最大迭代次数int n = 2; //适用于模型的最少数据个数double t = 0.01; //用于决定数据是否适应于模型的阀值int d = data_size*0.5; //判定模型是否适用于数据集的数据数目 //3.初始化输出量linearModel best_model; //最佳线性模型set<int> best_consensus_set; //记录一致点索引的setdouble best_error; //最小残差//4.运行RANSAC int status = ransac(Points, n, k, t, d, best_model, best_consensus_set, best_error);//5.输出cout << best_model.A << " " << best_model.B << " " << best_model.C << endl;return 0;
}
运行结果:
k = 50, n=2, t=0.01, d = data_size*0.5时
解法1:
您的代码已保存
答案正确:恭喜!您提交的程序通过了所有的测试用例解法2:
您的代码已保存
答案错误:您提交的程序没有通过所有的测试用例
case通过率为77.78%简单解法:
可将Estimate的步骤注释掉进行实验,根据consensus_set计算this_error
您的代码已保存
答案正确:恭喜!您提交的程序通过了所有的测试用例