RANSAC全程Random sample consensus，中文即“随机抽样一致算法”，该方法采用迭代的方式从一组包含离群（outlier或者错误数据）的被观测数据中估算出数学模型的参数，相比最小二乘方法，它融合了剔除不合格数据的思想，因此对于有部分错误数据的数据样本，能够更快更准的给出辨识结果。该算法首先由Fischler和Bolles 于1981提出，他们采用该方法来解决图像定位问题(LDP)。目前在图像以及辨识等领域广泛应用。

1 最小二乘算法的缺陷

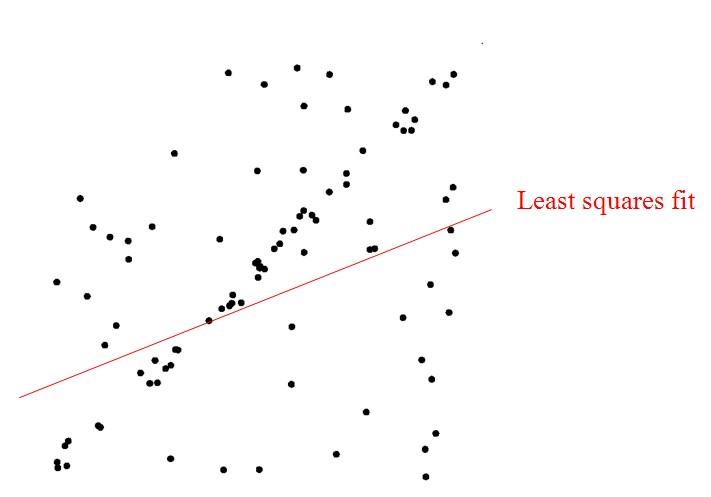
最小二乘方法，即通过最小化误差的平方和寻找数据的最佳函数匹配，广泛应用于数据辨识领域，但是其对于某些数据的拟合有一定的缺陷，最小二乘得到的是针对所有数据的全局最优，但是并不是所有数据都是适合去拟合的，也就是说数据可能存在较大的误差甚至差错，而这种差错的识别是需要一定的代价的，如下示意图（仅示意）就是一个典型的例子：

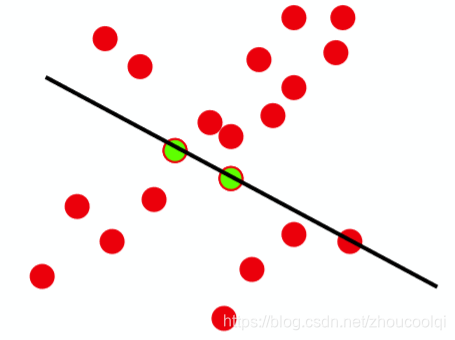
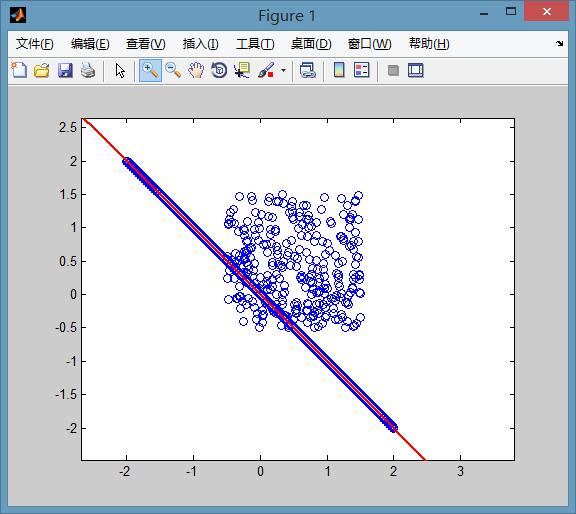
很显然，上述线性拟合的结果并不是我们想要的，我们真正需要的是一下拟合的效果：

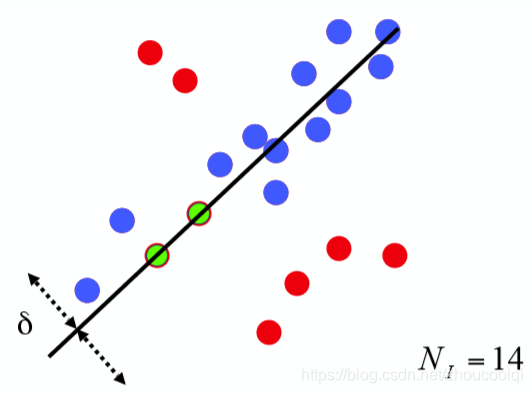
这正是RANSAC算法的拟合效果！因为剔除了不想被参与拟合的红点而选择在一定范围内的蓝点，这样保证了样本数据的干净，保证拟合效果更接近真实。

2 RANSAC算法

2.1 原理

通用的RANSAC算法的工作流程如下[2]:

给定如下:
data – 一组观测数据组.
model – 拟合模型（例如线性、二次曲线等等）.
n – 用于拟合的最小数据组数.
k – 算法规定的最大遍历次数.
t – 数据和模型匹配程度的阈值，在t范围内即inliers，在范围外即outliers.
d – 表示模型合适的最小数据组数.

返回如下:
bestFit – 一组最匹配的模型参数，即model的参数

以上前提中，data和model以及model的参数我们很容易理解，但是n、k、t、d的含义可能有点模糊，不妨先放一放，容后续慢慢理解。

函数体的伪代码如下：

参数初始化：
iterations = 0 /// 遍历次数
bestFit = nul
bestErr = something really large ///

/// 遍历
while iterations < k domaybeInliers := n /// 从数据中随机选择n个拟合的数据组maybeModel := model parameters fitted to maybeInliers /// 根据以上n个数据获得模型的参数alsoInliers := empty set  /// 初始化空数据组for every point in data not in maybeInliers do  /// 遍历：将处maybeInliers外的其他数据组一一与模型进行比较if point fits maybeModel with an error smaller than t /// 如果比较下来误差在t范围内，则调价到inliers集合中add point to alsoInliersend forif the number of elements in alsoInliers is > d then /// 如果当前得到的Inliers集合中的数据组数量大于d// This implies that we may have found a good model ///意味着该模型是个“好”模型（即好参数）// now test how good it is.betterModel := model parameters fitted to all points in maybeInliers and alsoInliersthisErr := a measure of how well betterModel fits these points/// 如果当前模型的与Inliers中数据的误差比之前得到的最小误差更小，则更新最小误差，/// 最优模型参数设置为当前模型参数if thisErr < bestErr thenbestFit := betterModelbestErr := thisErrend ifend ifincrement iterations  /// 继续遍历
end while

多看两边以上的以上的伪代码，相信应该是可以理解四个参数的含义了，如果还不理解，没关系，还有更实际的例子。往下看:

2.2 实例

以下是用MATLAB实现的一个采用RANSAC算法模型选为线性函数的函数与实例。

function [bestParameter1,bestParameter2] = ransac_demo(data,num,iter,threshDist,inlierRatio)% data: a 2xn dataset with #n data points% num: the minimum number of points. For line fitting problem, num=2% iter: the number of iterations% threshDist: the threshold of the distances between points and the fitting line% inlierRatio: the threshold of the number of inliers %% Plot the data pointsfigure;plot(data(1,:),data(2,:),'o');hold on;number = size(data,2); % Total number of pointsbestInNum = 0; % Best fitting line with largest number of inliersbestParameter1=0;bestParameter2=0; % parameters for best fitting linefor i=1:iter%% Randomly select 2 pointsidx = randperm(number,num); sample = data(:,idx);   %% Compute the distances between all points with the fitting line kLine = sample(:,2)-sample(:,1);% two points relative distancekLineNorm = kLine/norm(kLine);normVector = [-kLineNorm(2),kLineNorm(1)];%Ax+By+C=0 A=-kLineNorm(2),B=kLineNorm(1)distance = normVector*(data - repmat(sample(:,1),1,number));%% Compute the inliers with distances smaller than the thresholdinlierIdx = find(abs(distance)<=threshDist);inlierNum = length(inlierIdx);%% Update the number of inliers and fitting model if better model is found     if inlierNum>=round(inlierRatio*number) && inlierNum>bestInNumbestInNum = inlierNum;parameter1 = (sample(2,2)-sample(2,1))/(sample(1,2)-sample(1,1));parameter2 = sample(2,1)-parameter1*sample(1,1);bestParameter1=parameter1; bestParameter2=parameter2;endend%% Plot the best fitting linexAxis = -number/2:number/2; yAxis = bestParameter1*xAxis + bestParameter2;plot(xAxis,yAxis,'r-','LineWidth',2);
end%% Generate random data for test
data = 150*(2*rand(2,100)-1); data = data.*rand(2,100);
ransac_demo(data,2,100,10,0.1);

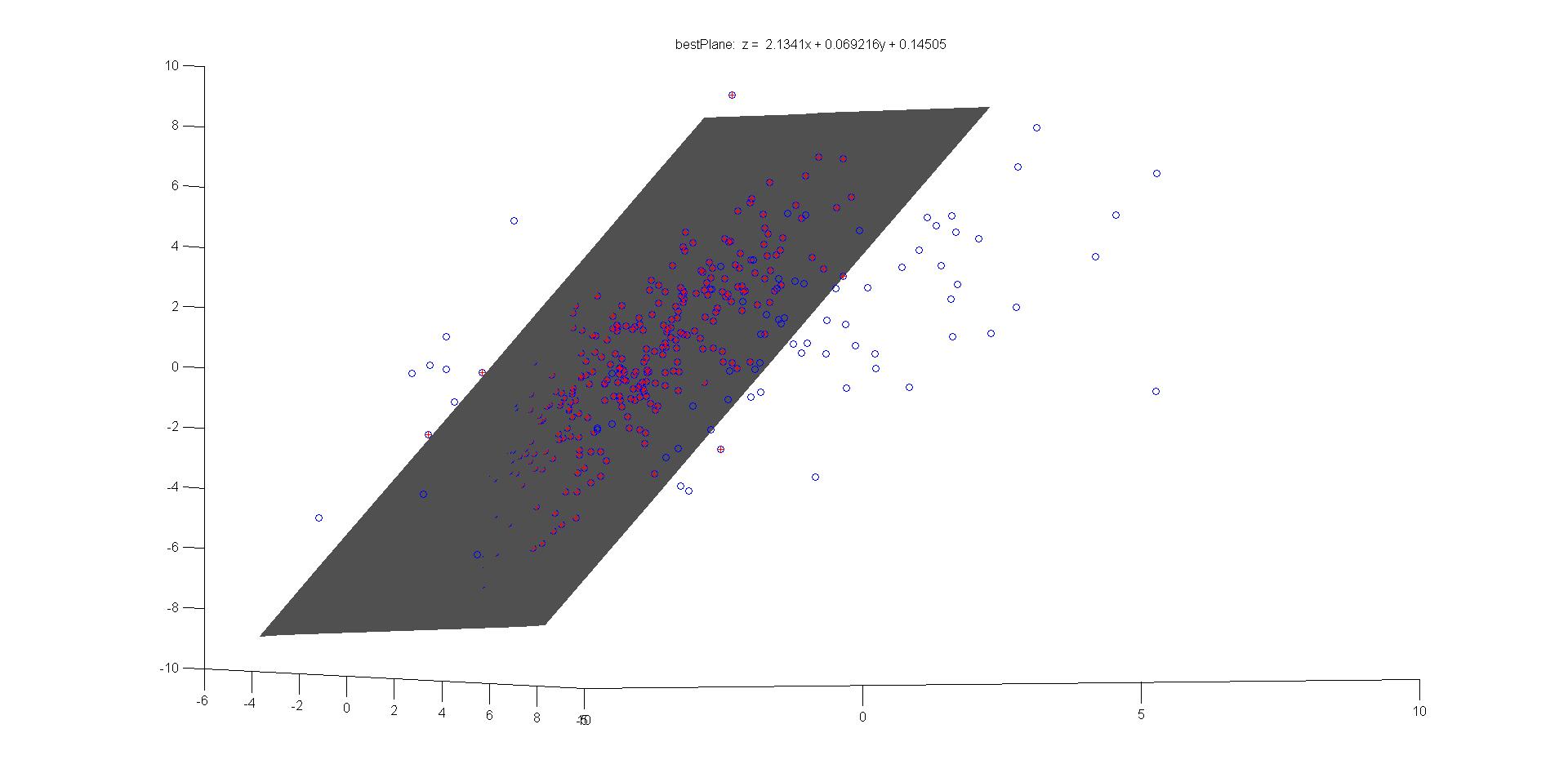
结果如下：

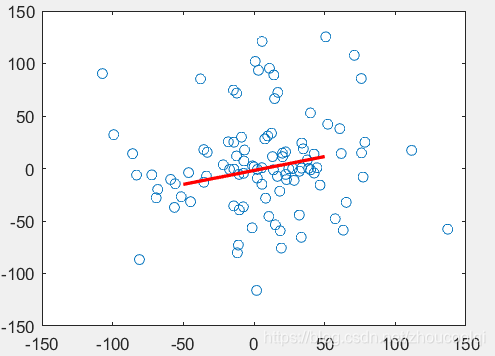
这里，数据(data )集随机产生的100组(x,y)数据集，模型(model)为y=ax+b,需要辨识的参数即a和b， 即n为2，遍历次数k为100（数据量本身较少，可以全部遍历），t为10，即只有满足到直线y=ax+b的距离小于10的点才会被认为是inliers，d指的是认定模型及参数为好的inliers集的最小数量值，这里采用比值表示，0.1表示100的十分之一即数据量达到10即可认为已经满足要求。

2.3 参数

可以看到，RANSAC算法除了选择合适的数据和模型外，还需要选择合适的4个参数n、k、t、d，其中n、t、d可根据经验得到，那么k可以根据如下公式计算:

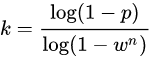
其中，$p$表示为RANSAC算法结果有用的概率，$w$为数据在inliers集中的概率，那么对于模型拟合一次需要的n个数据，其均在inliers集中的概率为$w^n$（放回取样概率），不在inliers集中的概率则为$1-w^n$，因此k次迭代的结果满足：

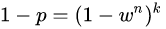
从而可有得到k的计算公式。

事实上在MATLAB中也存已有的函数ransac，该函数设计的更加通用，感兴趣的可以自己学习。

最后，本文的例子和原理主要参考自：《Random sample consensus》。

参考

1. 维基百科：《Random sample consensus》。
2. Martin A. Fischler and Robert C. Bolles (June 1981). “Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography”. Comm. of the ACM 24: 381–395. doi:10.1145/358669.358692.
3. MATLAB官网关于RANSAC的介绍: https://www.mathworks.com/discovery/ransac.html

感谢阅读