RANSAC介绍（Matlab版直线拟合+平面拟合）

本人邮箱：sylvester0510@163.com，欢迎交流讨论，
欢迎转载，转载请注明网址http://blog.csdn.net/u010128736/

一、RANSAC介绍

随机抽样一致算法（RANdom SAmple Consensus,RANSAC）,采用迭代的方式从一组包含离群的被观测数据中估算出数学模型的参数。维基百科中的RANSAC该算法最早由Fischler和Bolles于1981年提出。RANSAC算法假设数据中包含正确数据和异常数据（或称为噪声）。正确数据记为内点（inliers），异常数据记为外点（outliers）。同时RANSAC也假设，给定一组正确的数据，存在可以计算出符合这些数据的模型参数的方法。该算法核心思想就是随机性和假设性，随机性是根据正确数据出现概率去随机选取抽样数据，根据大数定律，随机性模拟可以近似得到正确结果。假设性是假设选取出的抽样数据都是正确数据，然后用这些正确数据通过问题满足的模型，去计算其他点，然后对这次结果进行一个评分。
RANSAC算法被广泛应用在计算机视觉领域和数学领域，例如直线拟合、平面拟合、计算图像或点云间的变换矩阵、计算基础矩阵等方面，使用的非常多。本文将在对RANSAC介绍完后，附两段直线拟合以及平面拟合的matlab代码。关于计算机视觉中基于RANSAC框架的矩阵求解问题，在OpenCV中都有对应的函数接口，如果以后有机会再把这个整理出来。

二、算法基本思想

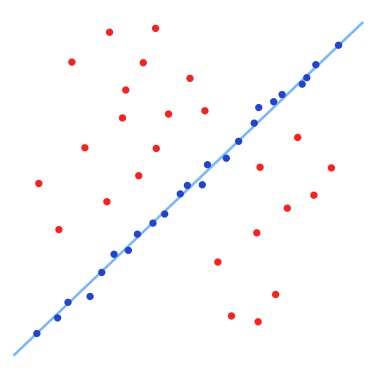
如下图所示，存在很多离散的点，而我们认为这些点构成了一条直线。当然，人眼能很清晰地拟合出这条直线，找到外点。但要让计算机找到这条直线，在很久之前是很难的，RACSAC的出现是通过数学之美解决这一难题的重要发明。
这里写图片描述

通过实例对算法基本思想进行描述：

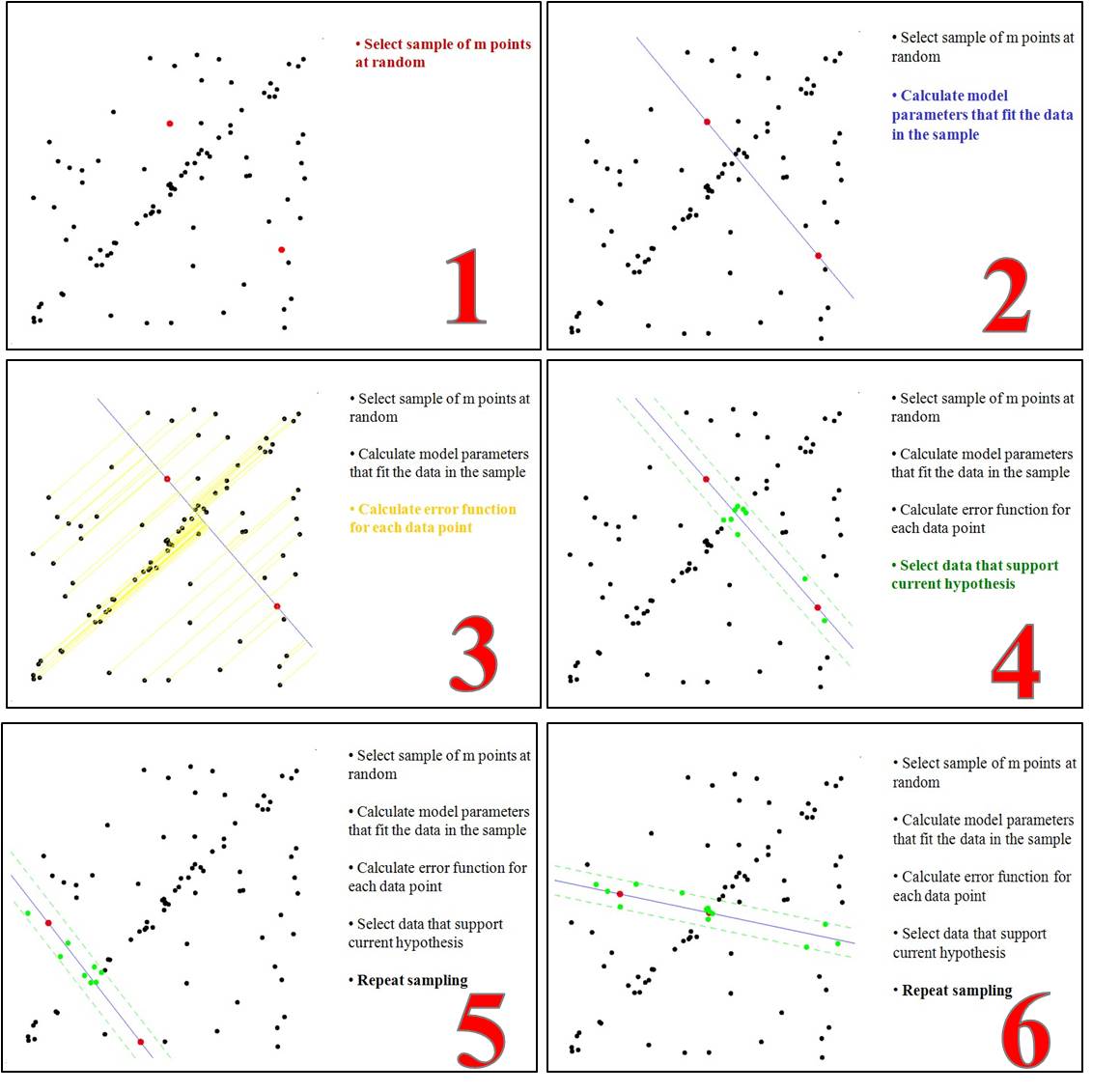
（1）首先，我们知道要得到一个直线模型，我们需要两个点唯一确定一个直线方程。所以第一步我们随机选择两个点。
（2）通过这两个点，我们可以计算出这两个点所表示的模型方程y=ax+b。
（3）我们将所有的数据点套到这个模型中计算误差。
（4）我们找到所有满足误差阈值的点，第4幅图中可以看到，只有很少的点支持这个模型。
（5）然后我们再重复（1）~（4）这个过程，直到达到一定迭代次数后，我们选出那个被支持的最多的模型，作为问题的解。如下图所示：
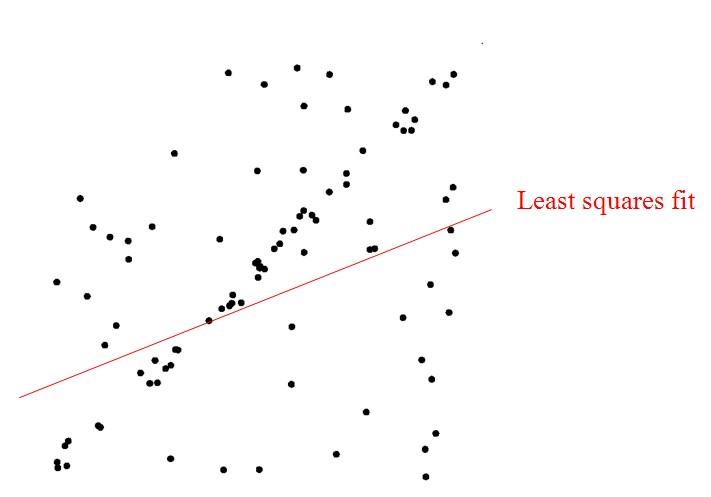
这里写图片描述

以上是对RANSAC算法的基本思想的介绍，我们可以发现，虽然这个数据集中外点和内点的比例几乎相等，但是RANSAC算法还是能找到最合适的解。试想一下，这个问题如果使用最小二乘法进行优化，由于噪声数据的干扰，我们得到的结果肯定是一个错误的结果，如下图所示。这是由于最小二乘法是一个将外点参与讨论的代价优化问题，而RANSAC是一个使用内点进行优化的问题。经实验验证，对于包含80%误差的数据集，RANSAC的效果远优于直接的最小二乘法。
这里写图片描述

三、RANSAC的数学推导

我们假设内点在整个数据集中的概率为t，即：

t = n i n l i e r s n i n l i e r s + n o u t l i e r s

$t = \frac{n_{inliers}}{n_{inliers} + n_{outliers}}$
确定该问题的模型需要n个点，这个n是根据问题而定义的，例如拟合直线时n为2，平面拟合时n=3，求解点云之间的刚性变换矩阵时n=3，求解图像之间的射影变换矩阵是n=4，等等。k表示迭代次数，即随机选取n个点计算模型的次数。P为在这些参数下得到正确解的概率。为方便表示，我们可以得到，n个点都是内点的概率为

tn $t^n$ ，则n个点中至少有一个是外点的概率为

1 - t n

$1-t^n$

（1−tn）k $（1-t^n）^k$ 表示k次随机抽样中都没有找到一次全是内点的情况，这个时候得到的是错误解，也就是：

P = 1 - (1 - t n) k

$P = 1 - (1-t^n)^k$
内点概率t是一个先验值，可以给出一些鲁棒的值。同时也可以看出，即使t给的过于乐观，也可以通过增加迭代次数k，来保证正确解的概率P。同样的，我们可以通过上面式子计算出来迭代次数k，即我们假设需要正确概率为P（例如我们需要99%的概率取到正确解），则：

k = l o g ( 1 - P ) l o g ( 1 - t n )

$k = \frac{log(1-P)}{log(1-t^n)}$

四、利用RANSAC拟合直线

clc;clear all;close all;%%%二维直线拟合
%%%生成随机数据
%内点
mu=[0 0];  %均值
S=[1 2.5;2.5 8];  %协方差
data1=mvnrnd(mu,S,200);   %产生200个高斯分布数据
%外点
mu=[2 2];
S=[8 0;0 8];
data2=mvnrnd(mu,S,100);     %产生100个噪声数据
%合并数据
data=[data1',data2'];
iter = 100; %%% 绘制数据点figure;plot(data(1,:),data(2,:),'o');hold on; % 显示数据点number = size(data,2); % 总点数bestParameter1=0; bestParameter2=0; % 最佳匹配的参数sigma = 1;pretotal=0;     %符合拟合模型的数据的个数for i=1:iter%%% 随机选择两个点idx = randperm(number,2); sample = data(:,idx); %%%拟合直线方程 y=kx+bline = zeros(1,3);x = sample(:, 1);y = sample(:, 2);k=(y(1)-y(2))/(x(1)-x(2));      %直线斜率b = y(1) - k*x(1);line = [k -1 b]mask=abs(line*[data; ones(1,size(data,2))]);    %求每个数据到拟合直线的距离total=sum(mask<sigma);              %计算数据距离直线小于一定阈值的数据的个数if total>pretotal            %找到符合拟合直线数据最多的拟合直线pretotal=total;bestline=line;          %找到最好的拟合直线end  end%显示符合最佳拟合的数据
mask=abs(bestline*[data; ones(1,size(data,2))])<sigma;    
hold on;
k=1;
for i=1:length(mask)if mask(i)inliers(1,k) = data(1,i);k=k+1;plot(data(1,i),data(2,i),'+');end
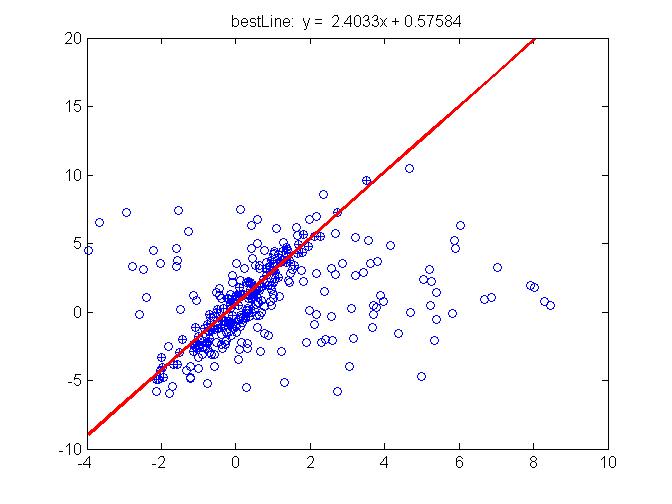
end%%% 绘制最佳匹配曲线bestParameter1 = -bestline(1)/bestline(2);bestParameter2 = -bestline(3)/bestline(2);xAxis = min(inliers(1,:)):max(inliers(1,:));yAxis = bestParameter1*xAxis + bestParameter2;plot(xAxis,yAxis,'r-','LineWidth',2);title(['bestLine:  y =  ',num2str(bestParameter1),'x + ',num2str(bestParameter2)]);

结果如图所示：

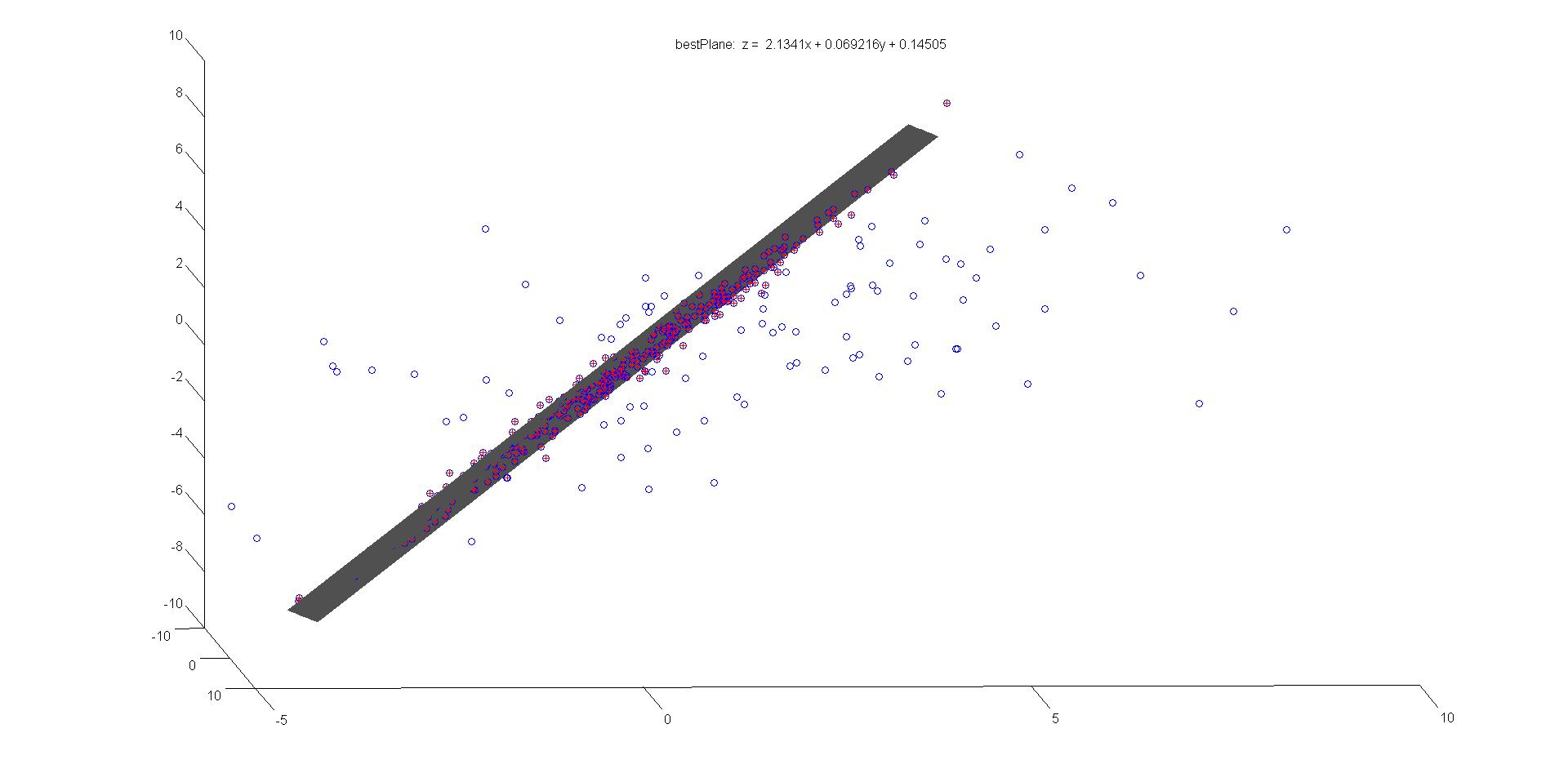
这里写图片描述

五、利用RANSAC拟合平面

clc;clear all;close all;%%%三维平面拟合
%%%生成随机数据
%内点
mu=[0 0 0];  %均值
S=[2 0 4;0 4 0;4 0 8];  %协方差
data1=mvnrnd(mu,S,300);   %产生200个高斯分布数据
%外点
mu=[2 2 2];
S=[8 1 4;1 8 2;4 2 8];  %协方差
data2=mvnrnd(mu,S,100);     %产生100个噪声数据
%合并数据
data=[data1',data2'];
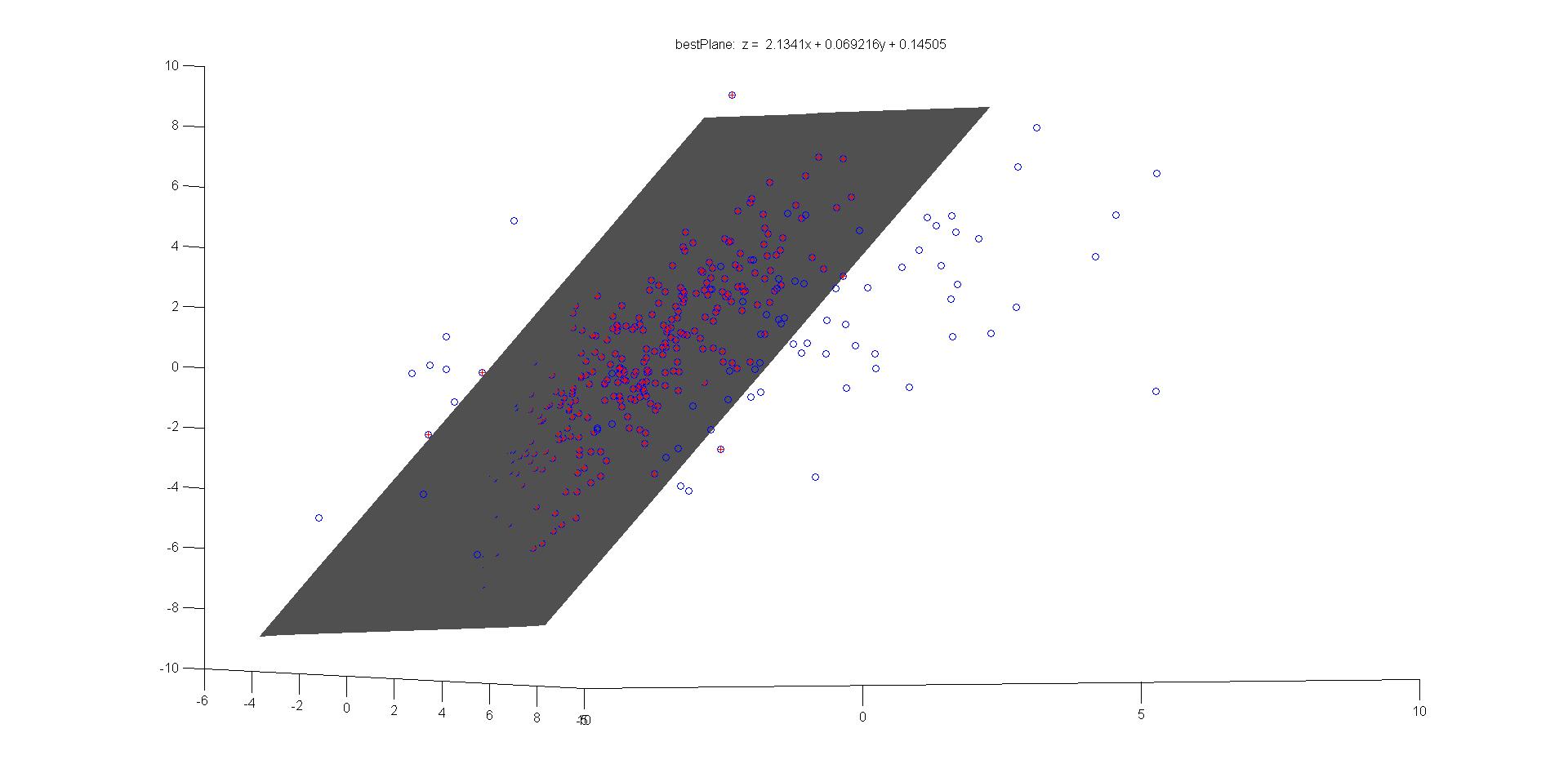
iter = 1000; %%% 绘制数据点figure;plot3(data(1,:),data(2,:),data(3,:),'o');hold on; % 显示数据点number = size(data,2); % 总点数bestParameter1=0; bestParameter2=0; bestParameter3=0; % 最佳匹配的参数sigma = 1;pretotal=0;     %符合拟合模型的数据的个数for i=1:iter%%% 随机选择三个点idx = randperm(number,3); sample = data(:,idx); %%%拟合直线方程 z=ax+by+cplane = zeros(1,3);x = sample(:, 1);y = sample(:, 2);z = sample(:, 3);a = ((z(1)-z(2))*(y(1)-y(3)) - (z(1)-z(3))*(y(1)-y(2)))/((x(1)-x(2))*(y(1)-y(3)) - (x(1)-x(3))*(y(1)-y(2)));b = ((z(1) - z(3)) - a * (x(1) - x(3)))/(y(1)-y(3));c = z(1) - a * x(1) - b * y(1);plane = [a b -1 c]mask=abs(plane*[data; ones(1,size(data,2))]);    %求每个数据到拟合平面的距离total=sum(mask<sigma);              %计算数据距离平面小于一定阈值的数据的个数if total>pretotal            %找到符合拟合平面数据最多的拟合平面pretotal=total;bestplane=plane;          %找到最好的拟合平面end  end%显示符合最佳拟合的数据
mask=abs(bestplane*[data; ones(1,size(data,2))])<sigma;    
hold on;
k = 1;
for i=1:length(mask)if mask(i)inliers(1,k) = data(1,i);inliers(2,k) = data(2,i);plot3(data(1,i),data(2,i),data(3,i),'r+');k = k+1;end
end%%% 绘制最佳匹配平面bestParameter1 = bestplane(1);bestParameter2 = bestplane(2);bestParameter3 = bestplane(4);xAxis = min(inliers(1,:)):max(inliers(1,:));yAxis = min(inliers(2,:)):max(inliers(2,:));[x,y] = meshgrid(xAxis, yAxis);z = bestParameter1 * x + bestParameter2 * y + bestParameter3;surf(x, y, z);title(['bestPlane:  z =  ',num2str(bestParameter1),'x + ',num2str(bestParameter2),'y + ',num2str(bestParameter3)]);