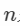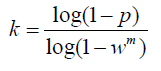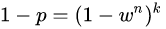精匹配——RANSAC算法思想及优缺点

---

前言

基于特征的图像匹配中会存在误匹配对，因此为提高匹配率，在粗匹配的基础上实现精匹配，可采用下面两种方法：

---

以下是本篇文章正对RANSAC的学习记录

一、RANSAC简介

RANSAC(RANdom SAmple Consensus随机采样一致性算法)，是在一组含有“外点”的数据中，不断迭代，最终正确估计出最优参数模型的算法。

• 主要解决样本中的外点问题，最多可处理50%的外点情况。
• 内点：符合最优参数模型的点。
• 外点：不符合最优参数模型的点，一般指的数据中的噪声或无效点，比如说匹配中的误匹配对和估计曲线中的离群点。
• 外点检测算法
• 应用：在计算机视觉的匹配问题中广泛应用，以寻找最佳的匹配模型，达到去除误匹配对，实现精匹配的效果。

二、RANSAC基本思想

1.步骤

 1. 在样本N中随机采样K个点 	2. 对这K个点进行模型拟合	3. 计算其他点到该拟合模型的距离，并设置阈值，若大于阈值，为外点，则舍弃，小于阈值，为内点，统计内点个数。阈值：为经验值，由具体应用和数据集决定。4. 然后以新的内点为基础，再次进行步骤2，得到新的拟合模型，迭代M次，选择内点数最多的模型，此时的模型为最优模型。5. 也可以在此基础上，选择出内点数最多的模型，然后对它进行重新估计，估计的时候可以采用最小二乘法来拟合。

2.迭代次数的公式

RANSAC算法中需要进行M次的迭代过程，且迭代的次数也是可以进行估算的。
————————————————————
1、n数据中内点所占的比例（内点的概率p）：

2、选取的K个点至少有一个是外点的概率：

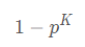
3、因此就能得到迭代M次的情况下，选取点都是外点的概率，进而得到迭代M次中，至少有一次选取点k个点都是内点的概率，也就是正确模型的概率：z一般要求满足大于95%即可。

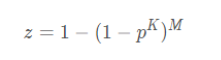
4、最终得到迭代次数M:
M = log(1-z)/log(1-p^k )
———————————————————

3.举例（拟合直线，拟合最佳单应性矩阵）

如下（示例1）：

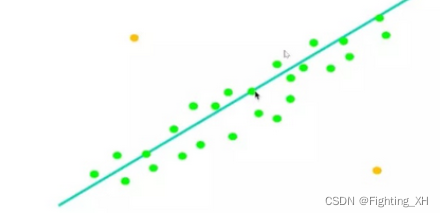
用RANSAC算法来拟合直线：

1、首先随机选取K=2个点，且两个点能拟合出一条直线

2、根据拟合直线，计算其他点到该拟合模型的距离，并设置阈值，其中绿色点为小于阈值的点，为内点，黄色的为外点，此时绿色内点为9。

3、然后通过此时的绿色内点，拟合出新的直线，再次计算该拟合新直线情况下的内点数目，此过程不断迭代，找到内点数最大的模型。

---

如下（示例2）：

用RANSAC算法来寻找最佳单应性矩阵H

在特征匹配中，我们最终要得到一个3*3的单应性矩阵。通常令h33=1来归一化矩阵，因此单应性矩阵有8个自由度h11-h32，求这八个未知数，至少要包含四个匹配点对。

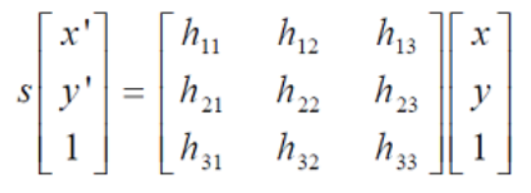
其中(x,y)表示目标图像角点位置,(x’,y’)为场景图像角点位置，s为尺度参数。

h33=1来归一化矩阵？
H单应性矩阵，描述两个平面的映射关系，平面中点的坐标是二维的，第三维取1，为了简单化，将h33=1，为最简单的非零值，来归一化矩阵。
——————
步骤：
通过SIFT算法已经进行了粗匹配，然后利用RANSAC算法来进精匹配。

1、首先在得到的匹配点中，随机选择4个匹配点对（不共线），其他匹配点为外点。2、根据4对内点计算单应性矩阵。3、根据此矩阵来测试其他匹配点(计算的是其他匹配点与该模型的投影误差），并设置阈值，若小于为新内点，若大于则为外点，也就是误匹配对，因此通过计算出的单应性矩阵，就能实现一次误匹配点的剔除。4、将所有的内点统计进行内点更新，在此基础上再次进行步骤3，迭代M次，最终得到含有内点最多的模型，此时模型为最优模型，也就是我们最终所需要的单应性矩阵。

———
大体步骤确定后，我们还需要进行两个参数的确定，阈值和迭代次数。
阈值：经验值
迭代次数：根据上述迭代次数M公式计算得到
——
如何用寻找到的单应性矩阵H来测试该模型下的其他匹配点？
根据代价函数计算，代价函数最小的模型为最优模型。
根据统计的内点数目，数目最多的为最优模型。

三、最小二乘法

1、最小二乘法的主要思想

通过确定未知参数（通常是一个参数矩阵），来使得真实值和预测值的误差（也称残差）平方和最小，其计算公式为

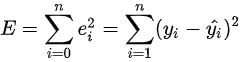
其中 yi是真实值，yi^是对应的预测值。
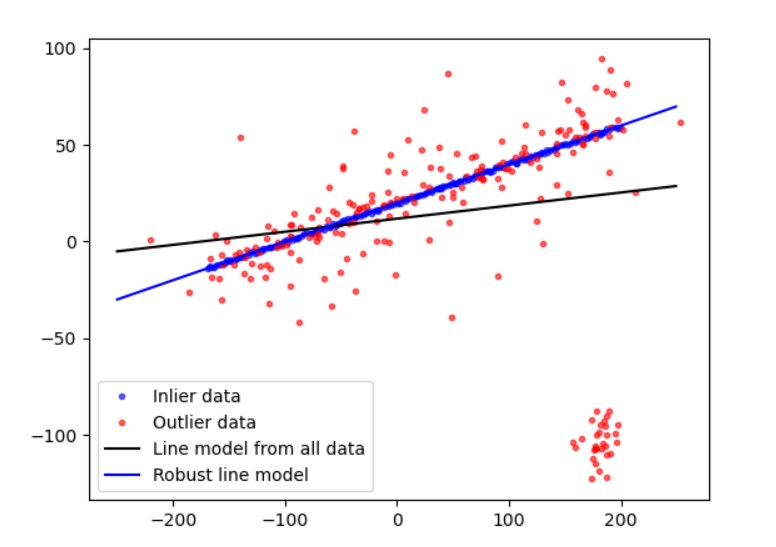
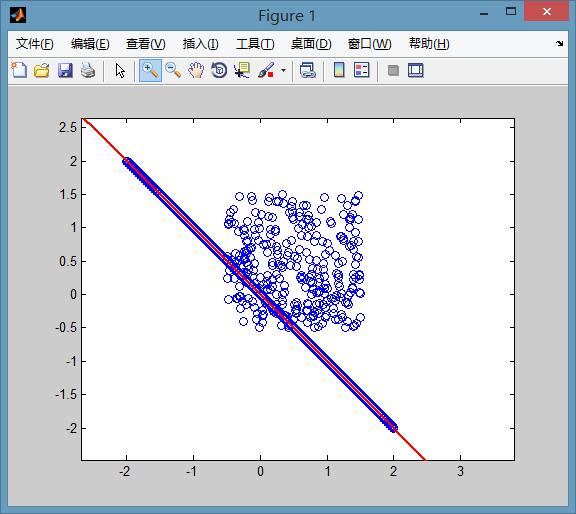
下图中，红色为数据点，蓝色为最小二乘法求得的最佳解，绿色即为误差

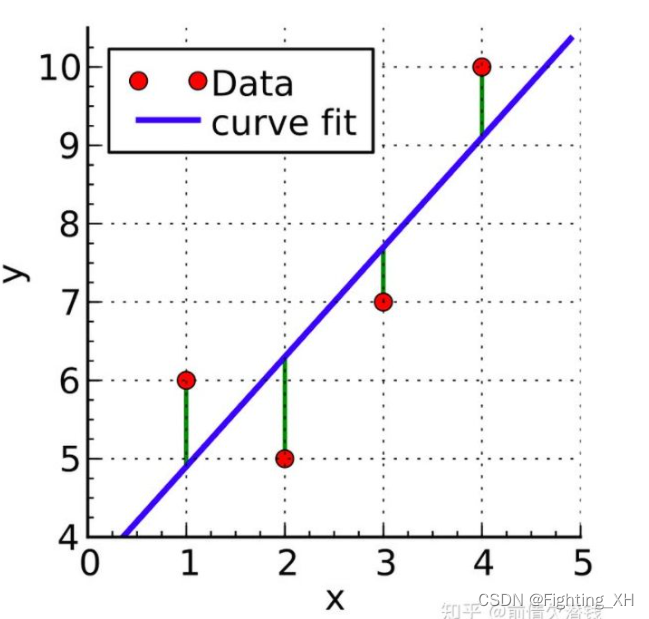
图中有四个数据点分别为：(1, 6), (2, 5), (3, 7), (4, 10)。显然，最佳解(3, 7)

2、最小二乘解

• 上面介绍了最小二乘法的公式：误差平方和

• 如下是2-范数：
  

• 根据这两个式子，进行最小二乘解的分析：

• 已知有一个这样的方程组：Ax=b 其中A∈Rm×n ; x∈Rn×k, b∈Rm×k

• 因此根据最小二乘法公式，那么求解最小二乘的问题即可等价于：

• 

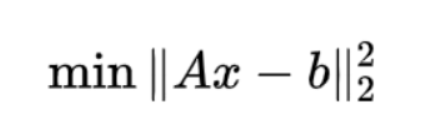
• 因此：

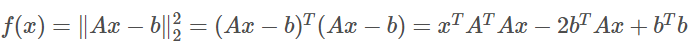
• 对 x 求导：
  

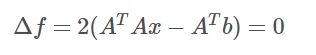
• 解得（最小二乘解）
  

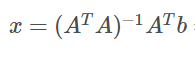
3、仿射变换最小二乘解的例子

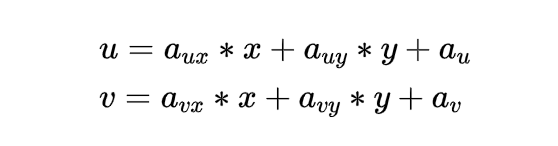
写成矩阵形式：

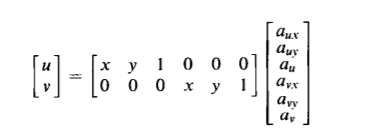
每对匹配点，提供两个约束。因此由N对点得到的等式组有2N个约束：

也可以简单写成：

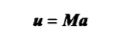
总平方误差：

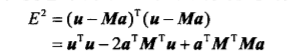
对每个参数求偏导，并令其为0，即

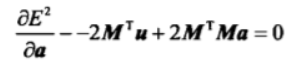
因此可得最小二乘解：

---

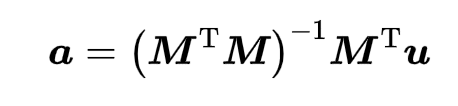
拓展小知识：

• 在线性回归中，通常我们使用均方误差来作为损失函数，同时均方误差可以看作是最小二乘法中的 E /m（m 为样本个数），所以最小二乘法求出来的最优解就是将均方误差作为损失函数求出来的最优解。
• 因此损失函数即可使用最小二乘法来表示
• 对于一维特征的样本，拟合函数为
  
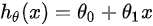
• 因此损失函数为：上标(i)表示第 i 个样本
  

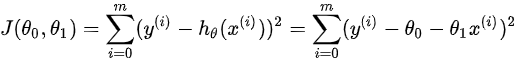
四、RANSAC 与 Least Squares Fit（最小二乘法）区别

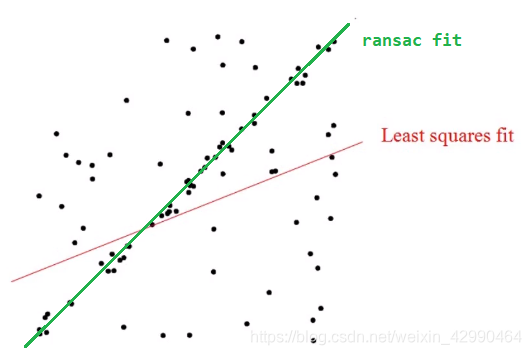
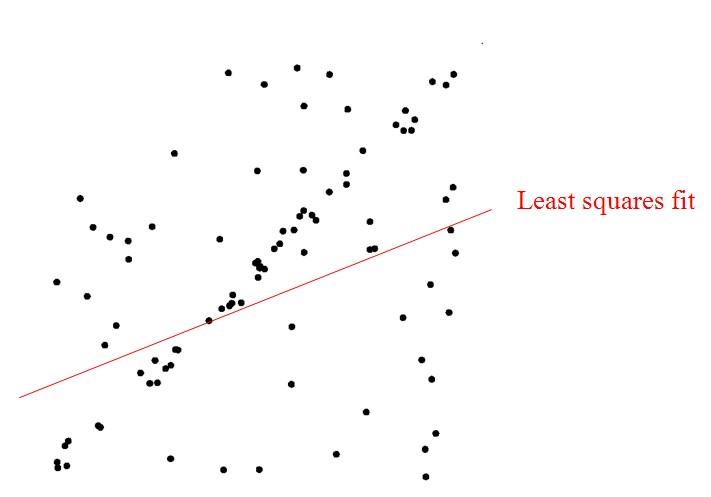
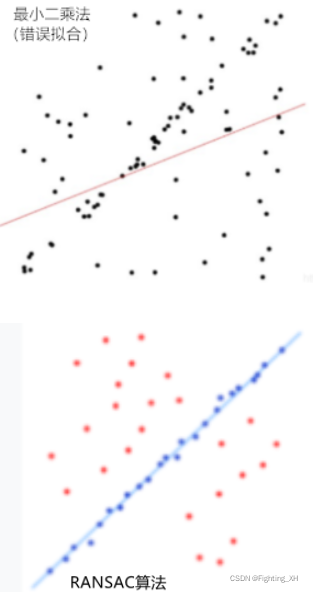
	RANSAC算法：适用于含有较大的噪声或无效点的情况最小二乘法：适用于误差比较小的情况

如下图所示，在误差比较大的情况下，肉眼也能看出拟合出的直线，但用最小二乘法拟合的直线却是错误的。而用RANSAC算法却能成功拟合。

五、RANSAC 算法的优缺点

优点：当数据中有大量的异常数据时，也能高精度的进行估计拟合。

缺点：对于异常数据超过50%的时候，拟合效果不佳。需要设置特定于问题的阈值。迭代次数若受到限制，那么达到迭代次数时拟合出来的模型可能并不是最佳模型。特定数据只能拟合出一个模型，一般多模型拟合采用霍夫变换。

六、Opencv实现RANSAC算法

//RANSAC算法
int main()
{Mat img_object = imread("./data/101.png", IMREAD_GRAYSCALE);Mat img_scene = imread("./data/100.png", IMREAD_GRAYSCALE);if (img_object.empty() || img_scene.empty()){cout << "Could not open or find the image!\n" << endl;return -1;}//-- Step 1: Detect the keypoints using SURF Detector, compute the descriptorsint minHessian = 800; // default: 400Ptr<SURF> surf = SURF::create(800);std::vector<KeyPoint> keypoints_object, keypoints_scene;Mat descriptors_object, descriptors_scene;surf->detectAndCompute(img_object, noArray(), keypoints_object, descriptors_object);surf->detectAndCompute(img_scene, noArray(), keypoints_scene, descriptors_scene);//-- Step 2: Matching descriptor vectors with a FLANN based matcher// Since SURF is a floating-point descriptor NORM_L2 is usedPtr<DescriptorMatcher> matcher = DescriptorMatcher::create(DescriptorMatcher::FLANNBASED);std::vector< std::vector<DMatch> > knn_matches;matcher->knnMatch(descriptors_object, descriptors_scene, knn_matches, 2);//-- Filter matches using the Lowe's ratio testconst float ratio_thresh = 0.75f;std::vector<DMatch> good_matches;for (size_t i = 0; i < knn_matches.size(); i++){if (knn_matches[i][0].distance < ratio_thresh * knn_matches[i][1].distance){good_matches.push_back(knn_matches[i][0]);}}//-- Draw matchesMat img_matches;drawMatches(img_object, keypoints_object, img_scene, keypoints_scene, good_matches, img_matches, Scalar::all(-1),Scalar::all(-1), std::vector<char>(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);//-- Localize the objectstd::vector<Point2f> obj;std::vector<Point2f> scene;for (size_t i = 0; i < good_matches.size(); i++){//-- Get the keypoints from the good matchesobj.push_back(keypoints_object[good_matches[i].queryIdx].pt);scene.push_back(keypoints_scene[good_matches[i].trainIdx].pt);}vector<uchar>inliers;Mat H = findHomography(obj, scene, inliers, RANSAC);//-- Draw matches with RANSACMat img_matches_ransac;std::vector<DMatch> good_matches_ransac;for (size_t i = 0; i < inliers.size(); i++){if (inliers[i]){good_matches_ransac.push_back(good_matches[i]);}}drawMatches(img_object, keypoints_object, img_scene, keypoints_scene, good_matches_ransac, img_matches_ransac, Scalar::all(-1),Scalar::all(-1), std::vector<char>(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);namedWindow("img_matches", WINDOW_NORMAL);imshow("img_matches", img_matches);imwrite("img_matches.jpg", img_matches);namedWindow("img_matches_ransac", WINDOW_NORMAL);imshow("img_matches_ransac", img_matches_ransac);imwrite("img_matches_ransac.jpg", img_matches_ransac);waitKey();return 0;
}

效果图：

参考博文

————————

所有无聊的事情都会衍生出很多细节让你觉得它复杂而有趣，投入其中而浑然不知其无聊的本质。
–王小波