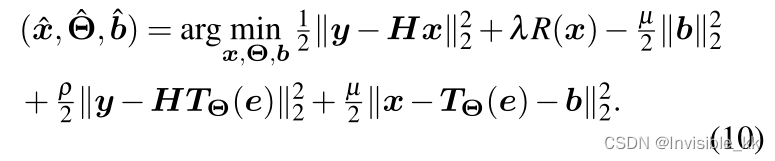前言

  本篇博客记录一下自己根据对论文 GRIM: A General, Real-Time Deep Learning Inference Framework for Mobile Devices based on Fine-Grained Structured Weight Sparsity 中提到的ADMM算法的理解，给出了ADMM算法的推导过程，并在文章的末尾提供了实现的代码。

1. 交替方向乘子法

  交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)作为一种求解优化问题的计算框架，适用于求解凸优化问题。ADMM算法的思想根源可以追溯到20世纪50年代，在20世纪八九十年代中期存在大量的文章分析这种方法的性质，但是当时ADMM主要用于解决偏微分方程问题。1970年由 R. Glowinski 和 D. Gabay 等提出的一种适用于可分离凸优化的简单有效方法，并在统计机器学习、数据挖掘和计算机视觉等领域中得到了广泛应用。ADMM算法主要解决带有等式约束的关于两个变量的目标函数的最小化问题，可以看作在增广拉朗格朗日算法基础上发展的算法，混合了对偶上升算法(Dual Ascent)的可分解性和乘子法(Method of Multipliers)的算法优越的收敛性。相对于乘子法，ADMM算法最大的优势在于其能够充分利用目标函数的可分解性，对目标函数中的多变量进行交替优化。在解决大规模问题上，利用ADMM算法可以将原问题的目标函数等价地分解成若干个可求解的子问题，然后并行求解每一个子问题，最后协调子问题的解得到原问题的全局解。¹

  优化问题
$$\begin{gathered} minimizef(x)+g(z) \\ subjecttoAx+Bz=c \end{gathered}$$  其中，$x\in R^n,z\in R^m,A\in R^{p\times n},B\in R^{p\times m},c\in R^p$，构造拉格朗日函数为
$$L_p(x,z,\lambda )=f(x)+g(z)+{\lambda }^T(Ax+Bz-c)$$  其增广拉格朗日函数(augmented Lagrangian function)为
$$L_p(x,z,\lambda )=f(x)+g(z)+{\lambda }^T(Ax+Bz-c)+\frac{\rho }{2}||Ax+Bz-c|{|}^2$$  对偶上升法迭代更新
$$\begin{gathered} (x^{k+1},z^{k+1})=\underset{x,z}{\mathrm{argmin}}{L}_p(x,z,{\lambda }^k) \\ {\lambda }^{k+1}={\lambda }^k+\rho (A{x}^{k+1}+B{z}^{k+1}-c) \end{gathered}$$  交替方向乘子法则是在$(x,z)$一起迭代的基础上将$x,z$分别固定单独交替迭代，即
$$\begin{gathered} x^{k+1}=\underset{x}{\mathrm{argmin}}{L}_p(x,z^k,{\lambda }^k) \\ {z}^{k+1}=\underset{z}{\mathrm{argmin}}{L}_p(x^{k+1},z,{\lambda }^k) \\ {\lambda }^{k+1}={\lambda }^k+\rho (A{x}^{k+1}+B{z}^{k+1}-c) \end{gathered}$$  交替方向乘子的另一种等价形式，将残差定义为$r^k=A{x}^k+B{z}^k-c$，同时定义$u^k=\frac{1}{\rho }{\lambda }^k$作为缩放的对偶变量(dual variable)，有
$$({\lambda }^k{)}^T{r}^k+\frac{\rho }{2}||r^k|{|}^2=\frac{\rho }{2}||r^k+u^k|{|}^2-\frac{\rho }{2}||u^k|{|}^2$$  改写 ADMM 的迭代过程
$$\begin{gathered} x^{k+1}=\underset{x}{\mathrm{argmin}}\{f(x)+\frac{\rho }{2}||Ax+B{z}^k-c+u^k|{|}^2\} \\ {z}^{k+1}=\underset{z}{\mathrm{argmin}}\{g(z)+\frac{\rho }{2}||A{x}^{k+1}+Bz-c+u^k|{|}^2\} \\ {u}^{k+1}=u^k+A{x}^{k+1}+B{z}^{k+1}-c \end{gathered}$$

2. 论文中的表述

3. 对论文中的公式进行推导

  为便于推导公式，将论文中的进行简化，参数W和b简记为W，此时的优化问题变为
$$\begin{gathered} minimizef(W_i)+\sum _{i=1}^{N}g(Z_i) \\ subjectto{W}_i=Z_i,i=1,2,...,N \end{gathered}$$  构造拉格朗日函数为
$$L_p(w,z,\lambda )=f(w)+\sum g(z)+{\lambda }^T(w-z)$$  其增广拉格朗日函数为
$$L_p(w,z,\lambda )=f(w)+\sum g(z)+{\lambda }^T(w-z)+\sum \frac{\rho }{2}||w-z|{|}^2$$  交替方向乘子法：在(x, z)一起迭代的基础上将 x, z 分别固定，单独交替迭代，即
$$\begin{gathered} w^{k+1}=\underset{w}{\mathrm{argmin}}{L}_p(w,z^k,{\lambda }^k) \\ {z}^{k+1}=\underset{z}{\mathrm{argmin}}{L}_p(w^{k+1},z,{\lambda }^k) \\ {\lambda }^{k+1}={\lambda }^k+\sum \rho (w-z) \end{gathered}$$  定义一个对偶变量
$$u^k=\frac{1}{\rho }{\lambda }^k$$  改写ADMM的迭代过程
$$\begin{gathered} w^{k+1}=\underset{w}{\mathrm{argmin}}\{f(w)+\sum \frac{\rho }{2}||w-z^k+u^k|{|}^2\} \\ {z}^{k+1}=\underset{z}{\mathrm{argmin}}\{\sum g(z)+\sum \frac{\rho }{2}||w^{k+1}-z+u^k|{|}^2\} \\ {u}^{k+1}=u^k+w^{k+1}-z^{k+1} \end{gathered}$$

4. 代码流程

# 初始化参数Z和U
Z, U = initialize_Z_and_U(model)# 训练model，并更新X，Z，U，损失函数为admm loss
for epoch in range(epochs):for data, target in train_loader:optimizer.zero_grad()output = model(data)loss = admm_loss(model, Z, U, output, target)loss.backward()optimizer.step()W = update_W(model)Z = update_Z(W, U, percent)U = update_U(U, W, Z)# 对weight进行剪枝，返回 mask
mask = apply_prune(model, percent)# 对剪枝后的model进行finetune
finetune(model, mask, train_loader, test_loader, optimizer)

5. 主要函数实现

def admm_loss(args, device, model, Z, U, output, target):idx = 0loss = F.nll_loss(output, target)for name, param in model.named_parameters():if name.split('.')[-1] == "weight":u = U[idx].to(device)z = Z[idx].to(device)# 这里就是推导出来的admm的表达式loss += args.rho / 2 * (param - z + u).norm()return lossdef update_W(model):W = ()for name, param in model.named_parameters():if name.split('.')[-1] == "weight":W += (param.detach().cpu().clone(),)return Wdef update_Z(W, U, args):new_Z = ()idx = 0for w, u in zip(W, U):z = w + upcen = np.percentile(abs(z), 100*args.percent[idx])under_threshold = abs(z) < pcen# percent剪枝率，小于percent分位数的置为0z.data[under_threshold] = 0new_Z += (z,)idx += 1return new_Zdef update_U(U, W, Z):new_U = ()for u, w, z in zip(U, W, Z):new_u = u + w - znew_U += (new_u,)return new_Udef prune_weight(weight, device, percent):# to work with admm, we calculate percentile based on all elements instead of nonzero elements.weight_numpy = weight.detach().cpu().numpy()pcen = np.percentile(abs(weight_numpy), 100*percent)under_threshold = abs(weight_numpy) < pcen# 非结构化剪枝weight_numpy[under_threshold] = 0mask = torch.Tensor(abs(weight_numpy) >= pcen).to(device)return mask

6. dense vs. prune(finetune)

结束语

  对论文中算法的推导仅限于自己的理解，可能还存在一些问题，欢迎来评论区交流哦^_^

参考教程

---

1. 《分布式机器学习：交替方向乘子法在机器学习中的应用》---- 雷大江著 ↩︎