刚接触图像恢复问题，简单记录一下最近看论文刚弄懂的一个小问题

ADMM算法

ADMM（交替方向乘子法）是一种解决变量可分离凸优化问题的简单算法，具有求解速度快，收敛性能好的特点。ADMM可以将原问题转换为几个子问题，分别并行求解，最后协调各个子问题的解，得到原问题最优解。

算法流程

ADMM算法主要用于解决如下凸优化问题：
$$\begin{gathered} \underset{x,y}{\mathrm{argmin}}f(x)+g(y) \\ s.t.Ax+By=c \end{gathered}$$
其中，$x\in R^n$为目标函数$f(x)$ 的优化变量，$y\in R^m$为目标函数 $g(y)$ 的优化变量， $A\in R^{p\times n}$ ，$B\in R^{p\times m}$ ， $c\in R^p$ 。 函数$f$，$g$ 是凸函数。

1. 首先写出他的增广拉格朗日函数：
   $$L_{\rho }(x,y,\lambda )=f(x)+g(y)+{\lambda }^T(Ax+By-c)+\rho /2\Vert Ax+By-c{\Vert }_2^2,\rho >0$$
   $\lambda \in R^p$是拉格朗日乘子，$\rho$为惩罚参数且$\rho >0$。
2. 利用ADMM算法求解：
   $$\begin{gathered} x_{k+1}=\underset{x}{\mathrm{argmin}}{L}_{\rho }(x,y_k,{\lambda }_k) \\ {y}_{k+1}=\underset{y}{\mathrm{argmin}}{L}_{\rho }(x_{k+1},y,{\lambda }_k) \\ {\lambda }_{k+1}={\lambda }_k+\rho (A{x}_{k+1}+B{y}_{k+1}-c) \end{gathered}$$
   实际上就是将$x$和$y$的联合优化过程分开了。
3. 利用放缩对偶变量进行化简：
   根据向量乘法公式$\Vert a+b{\Vert }_2^2=\Vert a{\Vert }_2^2+2a^{T}b+\Vert b{\Vert }_2^2$得$2a^{T}b+\Vert b{\Vert }_2^2=\Vert a+b{\Vert }_2^2-\Vert a{\Vert }_2^2$，所以$L_{\rho }(x,y,\lambda )$中的线性项${\lambda }^T(Ax+By-c)$和二次项$\rho /2\Vert Ax+By-c{\Vert }_2^2$可以进行合并：
   $$\begin{gathered} {\lambda }^T(Ax+By-c)+\rho /2\Vert Ax+By-c{\Vert }_2^2 \\ \begin{array}{l}=\frac{\rho }{2}\left(2\frac{{\lambda }^T}{\rho }(Ax+By-c)+\Vert Ax+By-c{\Vert }_2^2\right)\\ =\frac{\rho }{2}(\Vert Ax+By-c+{\lambda }^T/\rho {\Vert }_2^2-\Vert \lambda /\rho {\Vert }_2^2\end{array} \end{gathered}$$
   由于最后一项$\Vert \lambda /\rho {\Vert }_2^2$与$x$，$y$无关，因此不影响$x$和$y$子问题的求解，可以在求解子问题时省略。
4. 令放缩对偶变量为$u=\lambda /\rho$，则ADMM算法可以改写为以下形式：
   $$\begin{gathered} x_{k+1}=\underset{x}{\mathrm{argmin}}f(x)+\rho /2\Vert Ax+B{y}_k-c+u_k{\Vert }_2^2 \\ {y}_{k+1}=\underset{x}{\mathrm{argmin}}g(y)+\rho /2\Vert A{x}_{k+1}+By-c+u_k{\Vert }_2^2 \\ {u}_{k+1}=u_k+A{x}_{k+1}+B{y}_{k+1}-c \end{gathered}$$
   论文中经常利用放缩形式的ADMM算法，而刚开始接触ADMM时并不知道这种形式，所以导致很长一段时间我没看懂论文里公式是怎么推导的，这里对他的推导进行了一个总结。

在压缩图像重建中的应用

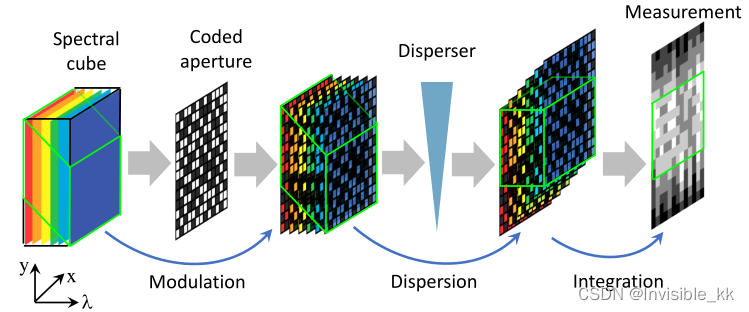
以上是压缩快照图像的成像过程，可以用以下公式来表示：
$$y=Hx+z$$
$y$代表观测图像，$x$代表理想的干净图像，$H$代表退化矩阵，是已知的，$z$代表观测噪声。
作者结合了深度图像先验以及去噪先验提出了以下重建模型：

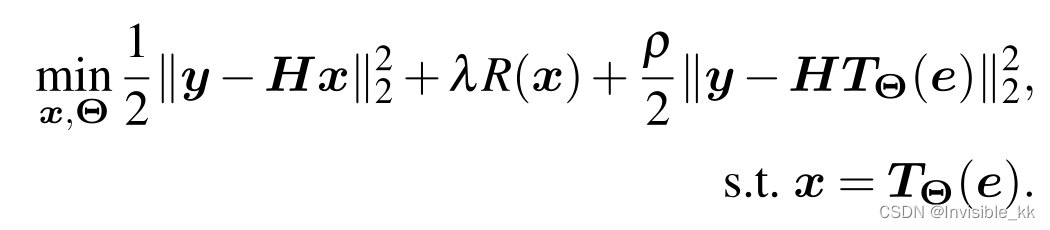
其中$T_{\Theta }(e)$是一个未训练的神经网络(参考论文Deep Image Prior)，用于提取图像先验，$R(x)$是去噪先验。以上优化模型可以利用ADMM算法进行求解，这里的第一项是保真项，后两项是先验项。然后引入放缩对偶变量$b$，就能得到下面的式子：

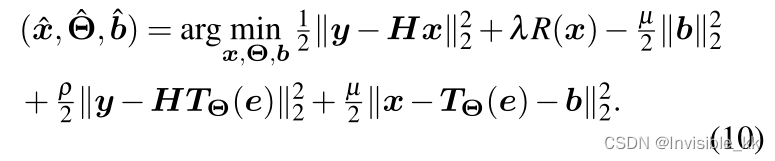
再利用ADMM算法就可以将上述问题解耦为关于$x,\Theta ,b$的三个子问题：
$$\begin{gathered} \begin{array}{l}\hat{\mathbf{\Theta }}=\underset{\Theta }{\mathrm{argmin}}\frac{\rho }{2}{\Vert \mathbf{y}-\mathbf{H}{\mathbf{T}}_{\mathbf{\Theta }}(\mathbf{e})\Vert }_2^2+\frac{\mu }{2}{\Vert \mathbf{x}-{\mathbf{T}}_{\mathbf{\Theta }}(\mathbf{e})-\mathbf{b}\Vert }_2^2\end{array} \\ \hat{\mathbf{x}}=\underset{\mathbf{x}}{\mathrm{argmin}}\frac{1}{2}\Vert \mathbf{y}-\mathbf{H}\mathbf{x}{\Vert }_2^2+\lambda R(\mathbf{x})+\frac{\mu }{2}{\Vert \mathbf{x}-{\mathbf{T}}_{\mathbf{\Theta }}(\mathbf{e})-\mathbf{b}\Vert }_2^2 \\ {\mathbf{b}}^{k+1}={\mathbf{b}}^k-\left({\mathbf{x}}^k-{\mathbf{T}}_{{\mathbf{\Theta }}^k}(\mathbf{e})\right) \end{gathered}$$
关于$\Theta$的子问题利用DIP网络求解，这个式子可以直接作为他的loss函数，关于x的子问题含有$R(x)$先验项，不便于直接求解，可以再利用ADMM算法进行分解，相当于ADMM里嵌套了一个ADMM，具体可以参考原论文。
论文链接: Self-supervised Neural Networks for Spectral Snapshot Compressive Imaging
参考网址：Anna的知乎回答：ADMM算法的详细推导过程是什么