*{margin:0;padding:0;}
body{background:url(img/bg.jpg);width:100%;height:100%;overflow:hidden;};
h1{width:277;height:76px;margin:30px auto 0;}
.xc-3D{width:100%;height:300px;background:#fff;margin-top:100px;position:relative;transform-style:preserve-3D;/*转变3D*/perspective:800px;//景深}
.xc-3D img{position:absolute;-webkit-box-reflect:below 0 -webkit-linear-gradient(top,rgba(0,0,0,0.1),rgba(0,0,0,0.5));transition:1s;}
.xc-3D img .forn{transform:rotateY(45deg);transfromZ(-100px);}
.xc-3D img .now{transform:rotateY(0deg);transfromZ(100px);}
.xc-3D img .last{transform:rotateY(-45deg);transfromZ(-100px);}









var imgL=$(.xc-3D img).length;//代表有几个img
var lastMin=Math.floor(imgL/2);//向下取整数得到中间那个 初始中间序列号
for(var i=0;i
if(i
$(".xc-3D img")eq(1).addClass("forn");
}else if(i>lastMin){
$(".xc-3D img")eq(1).addClass("last");
}else{
$(".xc-3D img")eq(1).addClass("now");
}
};
};
//控制位置
function mind(){
//浏览器宽度
var w_l=$(window).width();
var _left=w_l/2)-$(".xc-3D.now").width/2;
$(".xc-3D img.now").css({left:_left+"px"});
for(var i=0;i
//非常重要
$(".xc-3D img.now").eq(i).css(left:_left-(lastMin-i)*150+"px");
};
//把left存储起来
Left[i]=parseInt($(".xc-3D img").eq(i).css("left"));//把字符串转化为数字
}
$(.xc-3D img).click(funtion(){
//添加样式
for(var i=0;i
var nowMin=$(this).index();
if(i
$(".xc-3D img")eq(1).removeClass().addClass("forn");
}else if(i>nowMin){
$(".xc-3D img")eq(1).removeClass().addClass("last");
}else{
$(".xc-3D img")eq(1).removeClass.addClass("now");
};
};;
//确定位置
for(var i=0;i
Left[i]-=(nowMin-lastMin)*150;//为什么
//非常重要
$(".xc-3D img").eq(i).css({left:Left[i]+"px"});
};
lastMin=nowMin;//当前和初始值交替
})
css兼容,js兼容,渲染,底层 ,内核兼容
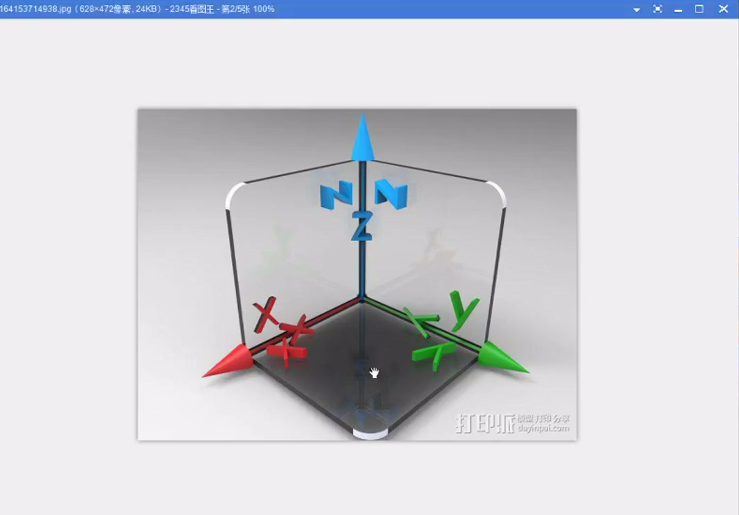
1投影
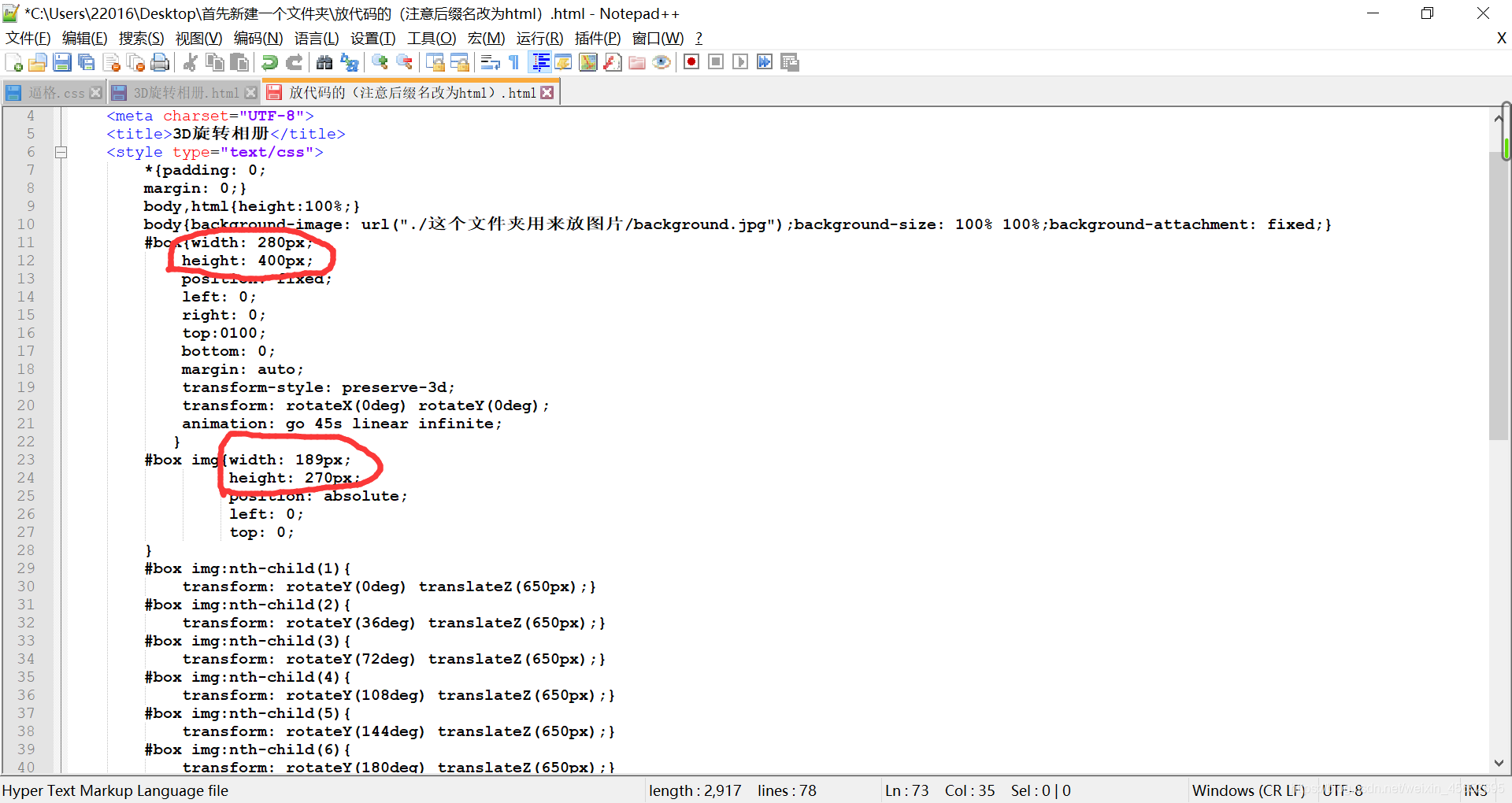
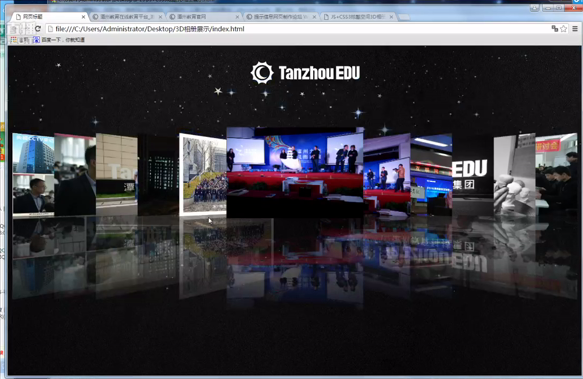
一款基于jQuery和CSS3炫酷3D旋转画廊特效插件
这是一款效果炫酷的jQuery和CSS3 3D旋转画廊特效插件.该3D画廊插件可以通过前后导航按钮来切换图片,效果就像旋转木马一样.它还带有点击放大图片,显示图片标题和用键盘操作等功能. 在线预览 ...
GJM :JS + CSS3 打造炫酷3D相册 [转载]
感谢您的阅读.喜欢的.有用的就请大哥大嫂们高抬贵手"推荐一下"吧!你的精神支持是博主强大的写作动力以及转载收藏动力.欢迎转载! 版权声明:本文原创发表于 [请点击连接前往] ,未经 ...
jQuery.smoove — jQuery和CSS3炫酷滚动页面内容元素动画特效插件
插件介绍: jQuery-smoove是一款jQuery和CSS3炫酷滚动页面内容元素动画特效插件.该内容元素动画插件在页面滚动到指定位置时,该位置的HTML元素会执行指定的CSS3动画特效,如旋转. ...
超酷3D照片展示效果
@{ Layout = null; } tf-8">
基于jQuery和CSS3炫酷图片3D旋转幻灯片特效
在线预览 源码下载 iPresenter是一款效果非常炫酷的jQuery和CSS3 3D旋转幻灯片特效插件.你可以使用它来制作产品展示.图片画廊或者各种幻灯片和轮播图特效.这款幻灯片插件的特点有: ...
Css3炫酷总结使用
先从CSS3的选择器说起: E F:所有的子孙元素: E>F: E中的子元素: E+F:E元素之后的最近的选择器: E~F:E中所以后面兄弟元素(CSS3 不包括自己本身,前面也不包括) att ...
随机推荐
【转】 各种 基于Unity3d 引擎的Android游戏优化 (drawcall)
合并纹理,减少贴图数量,合并网格,ui上减少不必要的层级叠加关系等 1. 更新不透明贴图的压缩格式为ETC 4bit,因为android市场的手机中的GPU有多种,每家的GPU支持不同的压缩格式 ...
eclipse - 自动换行
eclipse自动换行,设置的感觉不是很好用,可以从这个网址进行更新安装: http://ahtik.com/eclipse-update/
ServletContextListener 解析用法
ServletContext 被 Servlet 程序用来与 Web 容器通信.例如写日志,转发请求.每一个 Web 应用程序含有一个Context,被Web应用内的各个程序共享.因为Context可 ...
leetcode Palindrome Number python
class Solution(object): def isPalindrome(self, x): """ :type x: int :rtype: bool &quo ...
mysql 假设存在id则设数据自添加1 ,不存在则加入。java月份计算比較
INSERT INTO invite_rejectlog_num ...SrpingDruid数据源加密数据库密码
前言 在工作中遇到这样一个问题:开发过程中将数据库的账号.密码等信息配置在了一个单独的properties配置文件中(使用明文).但运维人员要求在配置文件中的密码一律不得出现明文. 环境 Spring ...
固定底部导航菜单-续集(BottomMenu-移动端V3.0)
固定底部导航菜单-续集(BottomMenu-移动端V3.0) 适应在客户端,点击弹出二级菜单.因为手机不支持hover.所以使用click点击实现弹出菜单,并且一级菜单聚焦变色,变化背景图片 核心c ...
python super()函数
super()函数是用来调用父类(超类)的一个方法 super()的语法: python 2 的用法: super(Class, self).xxx # class是子类的名称 class A(ob ...
35个让人惊讶的CSS3动画效果
1. Pure CSS Coke Can 2. Colorful Clock 3. jQuery DJ Hero 4. Animated Pricing Column 5. Slick jQuery ...
Hibernate- QBC查询方式
QBC查询方式 01.基本查询 02.组合查询 03.关联查询 04.分页查询 05.QBE查询 06.离线查询