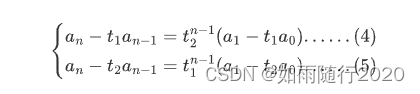斐波那契数列的四种解法

article/2025/10/12 16:07:05

题目描述

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从 1963 年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

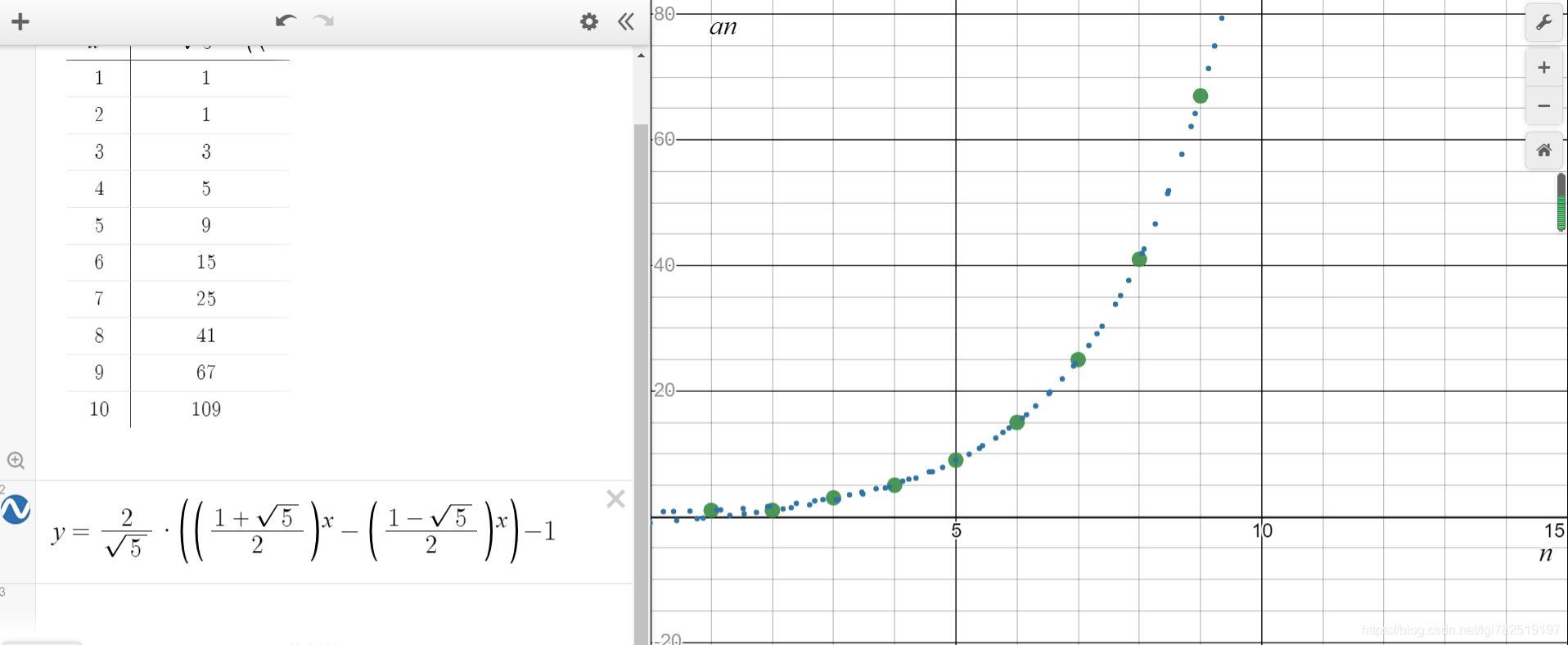
解法一：通项公式(O(1))

在这里插入图片描述
代码表示：

int ferbo(int n){return (sqrt(5)/5)*(pow((1+sqrt(5))/2,n)-pow((1-sqrt(5))/2,n));
}

解法二：递归求解（O(1.618^n)）

#include<iostream>
using namespace std;int fac(int x){if(x==1 || x==2){return 1;}if(x>2){return fac(x-1)+fac(x-2);}return 0;
}
int main()
{for(int i = 1; i<=20;i++){cout<<fac(i)<<" ";}cout<<endl;return 0;
}//1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765

解法三：动态规划（O（n））

#include<iostream>
using namespace std;
int fac[20];
int main()
{fac[1]=fac[2]=1;for(int i = 3;i<=20;i++){//此处使用变量a,b,c也可。 fac[i] = fac[i-1]+fac[i-2];}for(int i = 1;i <=20;i++){cout<<fac[i]<<" ";}cout<<endl;return 0; 
}
//1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765

解法四：矩阵快速幂(O(logn)）

矩阵公式

 F(n+1)=1*F(n)+1*F(n-1)F(n)=1*F(n)+0*F(n-1)F(n)=1*F(n-1)+1*F(n-2)F(n-1)=1*F(n-1)+0*F(n-2)

推导:
在这里插入图片描述
结论:只需要求出
,输出a[0][1] 或a[1] [0]都是F(n)的解.

快速幂

mod c只是为了防止数过大,不利于计算. 当数很小时,加不加没啥区别.
在这里插入图片描述
例如求a^n, (a=2)初始时,ans=1;

如果n=4,则计算步骤如下:

a=a*a=a^2   n=n/2=2
a=a*a=a^2 * a^2 = a^4  n=n/2=1
ans=ans*a=a^4

如果n=5,则计算步骤如下

因为n为奇数==>ans=ans*a    a=a*a=a^2   n=n/2=2
a=a*a=a^2 * a^2 = a^4  n=n/2=1
ans=ans^a=a^5

如果n=9,则计算步骤如下

因为n为奇数==>ans=ans*a    a=a*a=a^2   n=n/2=4
a=a*a=a^4   n=n/2=2
a=a*a=a^8   n=n/2=1
ans=ans^a=a^9

这样就把8次运算减少到了四次.而且也放置了数值过大的问题.

总结:当n为奇数时,ans=ans*a,这样相等于n-1变成了偶数.

快速幂代码

#include<iostream>
using namespace std;
int main() {int n,p,ans=1,a=2;cin>>n>>p;while(n) {if(n&1) {ans = ans * a %p;}a *= a % p;n/=2;}cout<<ans<<endl;return 0;
}
//16 1000000
//65536

矩阵快速幂

在这里插入图片描述

矩阵乘法:

原理：矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的栏数（column）和第二个矩阵的列数（row）相同时才有定义。一般单指矩阵乘积时，指的便是一般矩阵乘积。若A为m×n矩阵，B为n×p矩阵，则他们的乘积AB会是一个m×p矩阵。其乘积矩阵的元素如下面式子得出：
在这里插入图片描述
实现代码:

struct mat{int n, m;double data[MAXN][MAXN];
};int mul(mat& c, const mat& a, const mat& b){int i, j, k;if (a.m != b.n)return 0;c.n = a.n;c.m = b.m;for (i = 0; i < c.n; i++)for (j = 0; j < c.m; j++)for (c.data[i][j] = k = 0; k < a.m; k++)c.data[i][j] += a.data[i][k] * b.data[k][j];return 1;
}