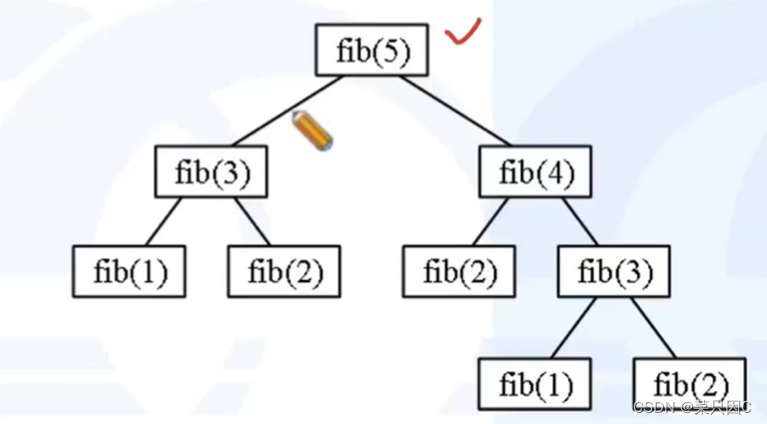
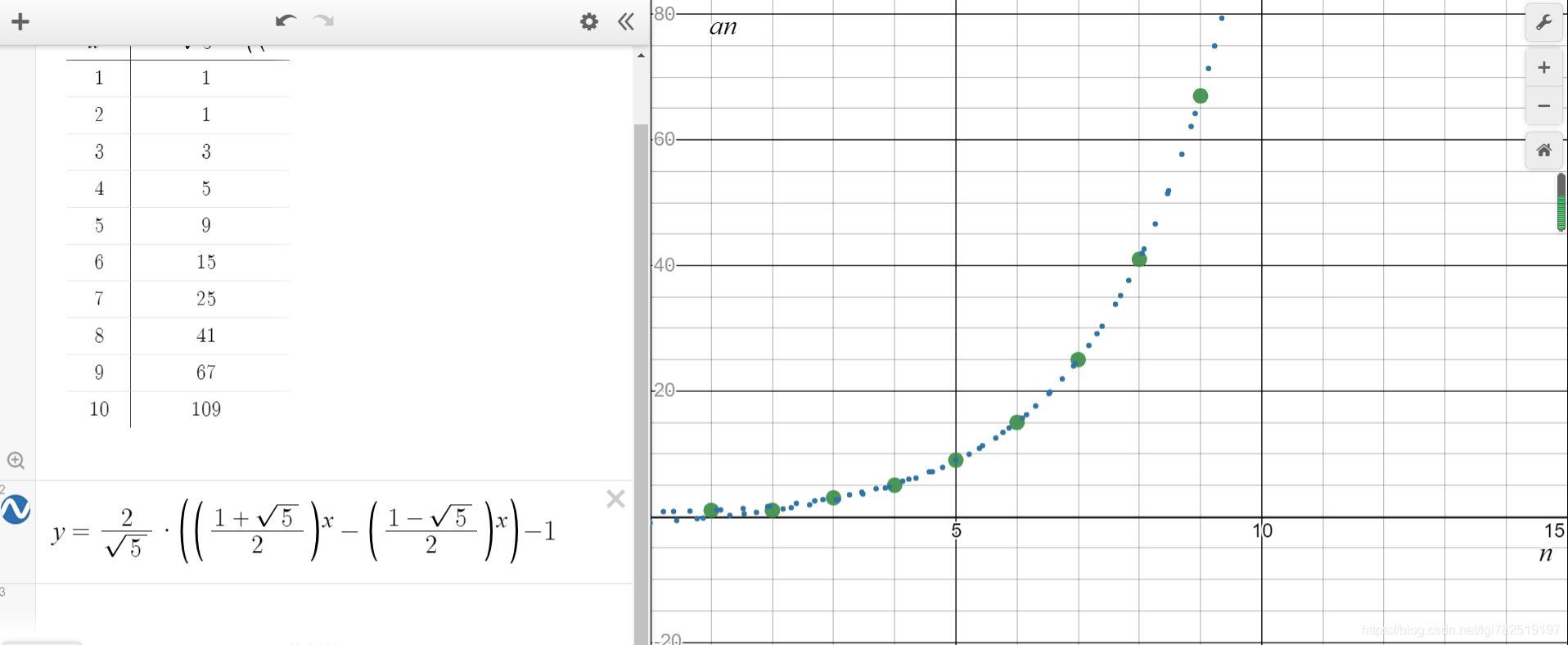
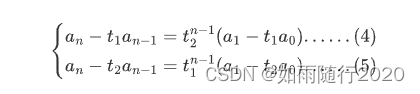斐波那契数列之python（5种方法）

article/2025/10/12 15:47:50

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波纳契数列以如下被以递归的方法定义：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=2，n∈N*）

1、递归方法

def fib_recur(n):if n<=1:return nelse:return fib_recur(n-1)+fib_recur(n-2)def ex(c):return int(c)X=input().strip().split()
N=list(map(lambda a:int(a), X))[0]for i in range(1, N):print(fib_recur(i),end=' ')

写法最简洁，但是效率最低，会出现大量的重复计算，时间复杂度O（1.618^n）,而且最深度1000

2、递推方法

def fib_loop(n):a,b=0,1for i in range(n+1):a,b=b,a+breturn afor i in range(20):print(fib_loop(i),end=' ')

递推法，就是递增法，时间复杂度是 O(n)，呈线性增长，如果数据量巨大，速度会越拖越慢

3、生成器

def fib_loop_while(n):a,b=0,1for i in range(0,n):a,b=b,a+byield afor i in fib_loop_while(20):print(i,end=' ')

怎么去解释这个生成器呢，我记得在以前的博客里面有提及到yield和yield from的区别，实际上更多只知道yield他是返回一个值而不退出这个函数执行。自然也就没有过多关注 fib_loop_while函数的返回对象类型是啥！

在这里系统解释一下：

1、带有yield关键字的函数对象他是返回一个列表list，list中的每个元素都是 yield返回的每一个值（每次执行yield输出值构成的列表）

2、带有yield的函数都被看成生成器，生成器是可迭代对象，且具备__iter__ 和 __next__方法，可以遍历获取元素
python要求迭代器本身也是可迭代的，所以我们还要为迭代器实现__iter__方法，而__iter__方法要返回一个迭代器，迭代器自身正是一个迭代器，所以迭代器的__iter__方法返回自身即可

4、类实现内部魔法方法

class Fibonacci(object):"""斐波那契数列迭代器"""def __init__(self,n):self.n=nself.a=0self.b=1self.cur=0def __next__(self):"""当使用next()函数调用时，就会获取下一个数"""if self.cur<self.n:self.a,self.b=self.b,self.a+self.bself.cur=self.cur+1return self.aelse:raise StopIteration #让他异常停止def __iter__(self):"""迭代器的__iter__ 返回自身即可"""return selfif __name__=="__main__":lst=list(map(int,input().strip().split()))M=lst[0]fib=Fibonacci(M)for n in fib:print(n,end=' ')

5、矩阵

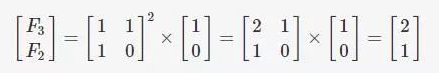
### 1
import numpy as npdef fib_matrix(n):res = pow((np.mat([[1, 1], [1, 0]])), n) * np.mat([[1], [0]]) #使用mat方法直接定义矩阵return res[0][0]for i in range(10):print(int(fib_matrix(i)), end=' ')
print('\n')### 2
# 使用矩阵计算斐波那契数列
def Fibonacci_Matrix_tool(n):Matrix = np.matrix([[1, 1], [1, 0]]) #matrix和mat函数等效# 返回是matrix类型return pow(Matrix, n)  # pow函数速度快于 使用双星好 **def Fibonacci_Matrix(n):result_list = []for i in range(0, n):result_list.append(np.array(Fibonacci_Matrix_tool(i))[0][0])return result_list# 调用
result=Fibonacci_Matrix(10)
for r in result:print(r,end=' ')

因为幂运算可以使用二分加速，所以矩阵法的时间复杂度为 O(log n)
用科学计算包numpy来实现矩阵法 O(log n)