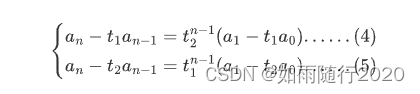关于斐波那契数列通项公式证明以及推广

article/2025/10/12 16:07:07

在我们中学的时候老师都会举一个著名的兔子繁殖的例子：一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？而这个问题就是著名的斐波那契数列。

具体可以表达为： $F_0=1,F_1=1,F_{n+1}=F_n+F_{n-1},n>=1$ ,

对于一个数列我们很自然地就会想要解出它的通项公式，可是我们该怎么做呢？

我们可以定义列向量 $f_n=\begin{bmatrix} F_{n-1}\\F_n \end{bmatrix}$ ,以及矩阵 $L=\begin{bmatrix} 0 &1 \\ 1 & 1 \end{bmatrix}$ .

于是我们容易得到： $Lf_n=f_{n+1}$ ,进一步的，我们可以得到， $L^{n-1}f_1=f_n$ ,

所以我们如果能够解出上面的公式我们就可以得到 $F_n$ 的公式。但是我们该怎么做呢？

这就不得不提到n阶矩阵的一个重要性质

n阶矩阵的特征值以及特征向量

对于一个性质良好的 $n \times n$ 的矩阵A，我们知道A乘一个 $n \times 1$ 的非零列向量还是一个 $n \times 1$ 的列向量，那么有没有可能 $Ax_1=\lambda x_1$ ,其中 $\lambda$ 是实数， $x_1$ 是 $n \times 1$ 列向量？答案是YES！

我们可以简单证明一下： $A=\begin{bmatrix} a_{11} & & & \\ &a_{22} & & \\ & & ...& \\ & & & a_{nn} \end{bmatrix}$ , $x_1=I_nx_1$ ,那么上面的式子相减得到 $\left ( A-I_n \lambda \right )x_1=0$ ,也就是说， $\begin{bmatrix} a_{11} -\lambda& & & \\ &a_{22} -\lambda& & \\ & & ...& \\ & & & a_{nn}-\lambda \end{bmatrix}$ 这个矩阵就是 $\left ( A-I_n \lambda \right )$ 。根据线性代数的知识我们容易知道其行列式必为零！我们将 $\lambda$ 称为特征值， $x_1$ 称为特征向量（注意在特征值确定的情况下特征向量并不唯一，但是他们会相互平行）

接下来就是线性代数的美妙之处了，对于 $n \times n$ 的矩阵A，有{ $x_1,x_2...x_m$ }个特征向量，

$A\left ( x_1+x_2+...x_n \right )={\lambda}x_1+{\lambda}x_2+...+{\lambda}x_n$ ,进一步的 $A^n\left ( x_1+x_2+...x_n \right )={\lambda}^nx_1+{\lambda}^nx_2+...+{\lambda}^nx_n$ 。

怎么样是不是很cool！

斐波那契数列通项公式具体证明

有了上面的数学基础我们马上就可以想到 $L^{n-1}f_1=f_n$ 和 $A^n\left ( x_1+x_2+...x_n \right )={\lambda}^nx_1+{\lambda}^nx_2+...+{\lambda}^nx_n$ 这个十分的类似，只要将 $L$ 的特征值以及特征向量解出来，并用特征向量的线性组合表达出 $f_1$ ，我们立刻就可以解出这个问题的答案。

下面是具体步骤：

$L=\begin{bmatrix} 0 &1 \\ 1 & 1 \end{bmatrix}$ ，设特征值为 $\lambda$ ,于是 $L-I_n{\lambda}=\begin{bmatrix} -{\lambda} &1 \\ 1 & 1-{\lambda} \end{bmatrix}$ , $det\left ( L-I_n{\lambda} \right )=0$ ,得到 ${-\lambda}{\times}\left ( {1-\lambda}\right )-1=0$ ,解得 ${\lambda}_1=\frac{1+\sqrt{5}}{2},{\lambda}_2=\frac{1-\sqrt{5}}{2}$ ,带入 $L-I_n{\lambda}=\begin{bmatrix} -{\lambda} &1 \\ 1 & 1-{\lambda} \end{bmatrix}$ ,解得两个不平行的特征向量 $x_1=\begin{bmatrix} 1\\ \frac{1+\sqrt{5}}{2} \end{bmatrix},x_2=\begin{bmatrix} 1\\ \frac{1-\sqrt{5}}{2} \end{bmatrix}$ ,接下来就是用 $x_1,x_2$ 的线性组合表达 $f_1=\begin{bmatrix} 1\\ 1 \end{bmatrix}$ ,也就是解出 $c1\times x_1+c2 \times x_2=f_1$ 中的c1,c2，解二元一次方程我们小学就已经学习过了，所以直接给答案 $c1=\frac{1+\sqrt{5}}{2\times \sqrt{5}},c2=-\frac{1-\sqrt{5}}{2\times \sqrt{5}}$ .

接下来就是激动人心的时刻了，运用公式 $A^n\left ( x_1+x_2+...x_n \right )={\lambda}^nx_1+{\lambda}^nx_2+...+{\lambda}^nx_n$ ，我们知道 $L^{n-1}f_1=f_n$ = $c1{\lambda}^{n-1}x_1+c2{\lambda}^{n-1}x_2$ ,而对于 $F_n$ 我们只关心其第二项，所以用 $x_1,x_2$ 的第二项进行运算，解得 $F_n=\frac{1}{\sqrt{5}}\left ( \left ( \frac{1+\sqrt{5}}{2} \right )^{n+1} -\left ( \frac{1-\sqrt{5}}{2} \right )^{n+1}\right )$ ,是不是出人意料？明明是由整数生成的数列最后的通项公式却蕴含着无理数，事实上，斐波那契数列和黄金分割比有着密切的关系，具体的大家可以自行查找资料。

最后是关于斐波那契数列的推广,对于数列 $F_0=f_0,F_1=f_1,F_{n+1}=aF_n+bF_{n-1},n>=1$ ，我们可以参考上面的做法定义一个列向量 $f_n=\begin{bmatrix} F_{n-1}\\F_n \end{bmatrix}$ ，以及矩阵 $L=\begin{bmatrix} 0 &1 \\ b & a \end{bmatrix}$ .同样的思路，同样的方法，大家可以自行尝试！（注意这个数列是从0开始的，如果想从1开始只需要将n+1改为n即可）