【NOIP2016提高组】蚯蚓

蚯蚓

题目背景

NOIP2016 提高组 Day2 T2

题目描述

本题中，我们将用符号表示对 c 向下取整，例如：

蛐蛐国最近蚯蚓成灾了！隔壁跳蚤国的跳蚤也拿蚯蚓们没办法，蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。

蛐蛐国里现在共有 n 只蚯蚓（n为正整数）。每只蚯蚓拥有长度，我们设第 i 只蚯蚓的长度为 ai (i=1，2，... ，n)，并保证所有的长度都是非负整数（即：可能存在长度为0的蚯蚓）。

每一秒，神刀手会在所有的蚯蚓中，准确地找到最长的那一只（如有多个则任选一个）将其切成两半。神刀手切开蚯蚓的位置由常数 p（是满足 0＜p＜1 的有理数）决定，设这只蚯蚓长度为 x ，神刀手会将其切成两只长度分别为的蚯蚓。特殊地，如果这两个数的其中一个等于 0 ，则这个长度为 0 的蚯蚓也会被保留。此外，除了刚刚产生的两只新蚯蚓，其余蚯蚓的长度都会增加 q（是一个非负整常数）。

蛐蛐国王知道这样不是长久之计，因为蚯蚓不仅会越来越多，还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物，但是救兵还需要 m 秒才能到来……（m为非负整数）

蛐蛐国王希望知道这 m 秒内的战况。具体来说，他希望知道：

m 秒内，每一秒被切断的蚯蚓被切断前的长度（有 m 个数）；
m 秒后，所有蚯蚓的长度（有 n+m 个数）。

蛐蛐国王当然知道怎么做啦！但是他想考考你……

输入格式

第一行包含六个整数 n，m，q，u，v，t，其中：n，m，q 的意义见【问题描述】；u，v，t 均为正整数；你需要自己计算 p=u/v（保证 0<u<v）；t 是输出参数，其含义将会在【输出格式】中解释。

第二行包含 n 个非负整数，为 a1，a2，... ，an，即初始时 n 只蚯蚓的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。

保证 1≤n≤10^5，0≤m≤7×10^6，0＜u＜v≤10^9，0≤q≤200，1≤t≤71，0≤ai≤10^8。

输出格式

第一行输出个整数，按时间顺序，依次输出第 t 秒，第 2t 秒，第 3t 秒，……被切断蚯蚓（在被切断前）的长度。

第二行输出个整数，输出 m 秒后蚯蚓的长度；需要按从大到小的顺序，依次输出排名第 t，第 2t，第 3t，……的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。即使某一行没有任何数需要输出，你也应输出一个空行。

请阅读样例来更好地理解这个格式。

样例数据 1

输入

3 7 1 1 3 1
3 3 2

输出

3 4 4 4 5 5 6
6 6 6 5 5 4 4 3 2 2

样例数据 2

输入

3 7 1 1 3 2
3 3 2

输出

4 4 5
6 5 4 3 2

样例数据 3

输入

3 7 1 1 3 9
3 3 2

输出

2

备注

【样例1说明】
在神刀手到来前：3 只蚯蚓的长度为 3，3，2。

【样例2说明】
这个数据中只有 t=2 与上个数据不同。只需在每行都改为每两个数输出一个数即可。
虽然第一行最后有一个 6 没有被输出，但是第二行仍然要重新从第二个数再开始输出。

【样例3说明】
这个数据中只有 t=9 与上个数据不同。
注意第一行没有数要输出，但也要输出一个空行。

1 秒后：一只长度为 3 的蚯蚓被切成了两只长度分别为 1 和 2 的蚯蚓，其余蚯蚓的长度增加了 1 。最终 4 只蚯蚓的长度分别为 (1,2)，4，3 。括号表示这个位置刚刚有一只蚯蚓被切断。
2 秒后：一只长度为 4 的蚯蚓被切成了 1 和 3 。5 只蚯蚓的长度分别为：2，3，(1,3)，4 。
3 秒后：一只长度为 4 的蚯蚓被切断。6 只蚯蚓的长度分别为：3，4，2，4，(1,3)。
4 秒后：一只长度为 4 的蚯蚓被切断。7 只蚯蚓的长度分别为：4，(1,3)，3，5，2，4。
5 秒后：一只长度为 5 的蚯蚓被切断。8 只蚯蚓的长度分别为：5，2，4，4，(1,4)，3，5。
6秒后：一只长度为5的蚯蚓被切断。9只蚯蚓的长度分别为：(1，4)，3，5，5，2，5，4，6。
7 秒后：一只长度为 6 的蚯蚓被切断。10只蚯蚓的长度分别为：2，5，4，6，6，3，6，5，(2,4)。

所以，7 秒内被切断的蚯蚓的长度依次为 3，4，4，4，5，5，6。7 秒后，所有蚯蚓长度从大到小排序为 6，6，6，5，5，4，4，3，2，2。

【数据规模与约定】
测试点 1～3 满足 m=0。
测试点 4～7 满足 n,m≤1,000。
测试点 8～14 满足 q=0，其中测试点 8～9 还满足 m≤105。
测试点 15～18 满足 m≤3×105。
测试点 19～20 没有特殊的约定，参见原始的数据范围。
测试点 1～12，15～16 还满足 v≤2 ，这意味着 u，v 的唯一可能的取值是 u=1，v=2，即 p=0.5。这可能会对解决问题有特殊的帮助。

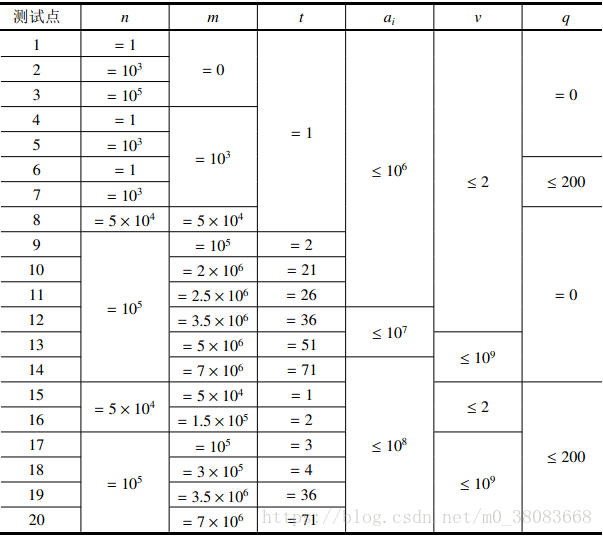
每个测试点的详细数据范围见下表。

题意：

初始时有 $n$ 个非负整数，进行 $m$ 次操作，每次依次：将其中最大的数 $x$ 移除，将剩下的每个数都增加 $q$ ，加入两个新数⌊ $px$ ⌋和 $x$ -⌊ $px$ ⌋ $(0<p<1,q>=0)$

没 $t$ 次操作输出这次被移除的数。最后好药输出大小排名为 $t$ 的倍数的数。保证每种输出的数不会超过 $10^{5}$

解析：

70分：

可以用优先队列实现，但是要优化一下。考虑每次取出一个最大值这个操作，堆来维护比较方便，但是每次加上一个 $q$ 似乎不好处理。我们考虑增加一个全局变量 $tag$ ，表示每个数都需要加上 $tag$ ，这样就可以避免对于堆中所有元素增加，而只需把每次新的两个元素减去 $q$ ，再放入堆中即可。具体做法：系统堆维护，每次取出最大元素，然后加上 $tag$ ，得到真实值，算出两个新元素值， $tag$ 加上 $q$ ，两个新元素值减去 $tag$ ，丢入堆中。

100分：

建立三个队列A，B，C，初始时A中元素为初始的数从大到小排序，B和C为空。每次操作时，从三个队列的队首（如果有）找出一个最大的元素出队，给最大的元素加上 $tag$ 即为实际的最大值 $x$ 。然后，将⌊ $px$ ⌋减去 $tag$ 插入到B的队尾，将 $x$ -⌊ $px$ ⌋减去 $tag$ 插入到C的队尾。所有操作完成后，通过类似归并的操作即可得到了从大到小排序的所有剩余的数。

这个算法的正确性并不显然，因为后一次操作与前一次操作移除的数的大小关系没有必然联系，也就是说你不能确定三个队首就是当前前三大的数。

我们一次考虑相邻的两个操作，设其中被移除的数分别为 $x1$ 和 $x2$ ，则有 $x1>=x2-q$ ，设加入⌊ $px_{1}$ ⌋和 $x$ -⌊ $px_{1}$ ⌋时维护的变量为 $tag$ ，则加入⌊ $px_{2}$ ⌋和 $x$ -⌊ $px_{2}$ ⌋时维护的变量为 $tag+q$ 。

对于队列B，两次操作中入队的数分别为⌊ $px_{1}$ ⌋ $-y$ 与⌊ $px_{2}$ ⌋ $-(y+q)$ 。由于 $x1>=x2-q$ ，所以⌊ $px_{1}$ ⌋ $>=$ ⌊ $px_{2}$ ⌋ $-q$ ，所以⌊ $px_{1}$ ⌋ $-y$ $>=$ ⌊ $px_{2}$ ⌋ $-(y+q)$ 。保证了实际入队的前面的数总是不小于后面的数。

对于队列C同理。

时间复杂度 $O(nlog_{n}+n+m)$ 。

PS：注意开 $long long$

代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int Max=7000100;
int n,m,u,v,q,t,h1=1,t1,h2=1,t2,h3=1,t3,sum,x,pre,num;
int ans[Max],q1[Max],q2[Max],q3[Max];
inline int get_int()
{int x=0,f=1;char c;for(c=getchar();(!isdigit(c))&&(c!='-');c=getchar());if(c=='-') {f=-1;c=getchar();}for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+c-'0';return x*f;
}
inline void print(int x){if(x > 9) print(x/10);putchar(x%10+'0');}
inline bool comp(const int &a,const int &b){return a>b;}
inline int calc(int x){return x*u/v;}
inline void solve()
{for(int i=1;i<=m;i++){num=max(q1[h1],max(q2[h2],q3[h3]));if(q1[h1]==num) h1++;else if(q2[h2]==num) h2++;else h3++;x=num+sum;sum+=q;if(!(i%t)) print(x),putchar(' ');num=calc(x),pre=x-num;q2[++t2]=num-sum,q3[++t3]=pre-sum; }
}
signed main()
{n=get_int(),m=get_int(),q=get_int(),u=get_int(),v=get_int(),t=get_int();memset(q1,-0x3f3f3f,sizeof(q1)),memset(q2,-0x3f3f3f,sizeof(q2)),memset(q3,-0x3f3f3f,sizeof(q3));for(int i=1;i<=n;i++) q1[i]=get_int();sort(q1+1,q1+n+1,comp);solve(),putchar('\n');for(int i=1;i<=n+m;i++){x=max(q1[h1],max(q2[h2],q3[h3]));if(q1[h1]==x) h1++;else if(q2[h2]==x) h2++;else h3++;if(!(i%t)) print(x+sum),putchar(' ');}return 0;
}