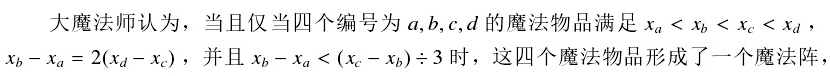[NOIP2016 普及组] 魔法阵

article/2025/9/27 19:34:11

[NOIP2016 普及组] 魔法阵 - 洛谷

题意分析

给定一个四元组，四个数分别为a,b,c,d，满足以下条件：

1.a<b<c<d

2.b-a=2*(d-c)

3.b-a=(c-b)/3 //注意是实除

现在给你一个序列X，请你求出序列X中每个数分别作为a,b,c,d的个数。

算法一：暴力枚举（PTS 35）

直接进行一个暴力的打，枚举a,b,c,d，判断是否满足条件，再用四个数组分别记录个数。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
int n,m;
int maho[40010];
bool check(int a,int b,int c,int d)
{if(a>=b||b>=c||c>=d) return false;if((b-a)!=2*(d-c)) return false;if(3*(b-a)>=(c-b)) return false;return true;
}
struct node{int aa,bb,cc,dd;
}h[1000010];
int main()
{memset(h,0,sizeof(h));scanf("%d%d",&n,&m);for(int i=1;i<=m;++i){scanf("%d",&maho[i]);}for(int d=1;d<=m;++d){for(int c=1;c<=m;++c){for(int b=1;b<=m;++b){for(int a=1;a<=m;++a){if(check(maho[a],maho[b],maho[c],maho[d])) {h[a].aa++;h[b].bb++;h[c].cc++;h[d].dd++;}}}}}for(int i=1;i<=m;++i){printf("%d %d %d %d\n",h[i].aa,h[i].bb,h[i].cc,h[i].dd);}return 0;
}

时间复杂度：O（n*n*n*n）

~~ps：这能给35分已经算是施舍了吧。。。~~

算法二：暴力优化（PTS 55）

不难想到：由a<b<c<d条件可知满足条件的四元组是单调递增的，因此我们不妨现将X排序，减少循环量。（记得记录每个数在原来X序列中的位置，输出时用）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
int n,m;
struct nn{int val,pos;
}maho[40010];
bool check(int a,int b,int c,int d)
{if(a<b&&b<c&&c<d) if((b-a)==2*(d-c)) if((b-a)<(c-b)/3.0) return true;return false;
}
int h[1000010][5];
bool cmp(nn a,nn b)
{if(a.val==b.val) return a.pos < b.pos;else return a.val < b.val;
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;++i){scanf("%d",&maho[i].val);maho[i].pos=i;}sort(maho+1,maho+m+1,cmp);for(int a=1;a<=m;++a){for(int b=a+1;b<=m;++b){for(int c=b+1;c<=m;++c){for(int d=c+1;d<=m;++d){if(check(maho[a].val,maho[b].val,maho[c].val,maho[d].val)) {h[maho[a].pos][1]++;h[maho[b].pos][2]++;h[maho[c].pos][3]++;h[maho[d].pos][4]++;}}}}}for(int i=1;i<=m;++i){printf("%d %d %d %d\n",h[i][1],h[i][2],h[i][3],h[i][4]);}return 0;
}

时间复杂度：比纯暴力算法快一点，不过还是O（n*n*n*n）级别的。

~~ps：蒟蒻在此止步。。。。~~

算法三：数学计算优化（PTS 100）

毕竟给的三个条件都是一个式子，我们可以活用数学知识来将这三个式子简化。

本题简化的基本思路：用已知数表示未知数

假设t = d - c

则b - a = 2 * t

则c - b >6 * t

所以我们不妨设c - b = 6 * t + k （k > 0）

则此时可以求出：

A点到B点之间的距离为2 * t

B点到C点之间的距离为6 * t + k

C点到D点之间的距离为t

再结合条件一，我们可以得到下面一张简图。

~~很简陋对吧（技术力低下++）~~

浅显の分析

到现在大家应该都看出来了应该枚举t并用t表示数。

先弱弱地看一波数据范围。。

40000......emmmm，看来必须是O（n）的算法了呢~

枚举之前，要先算出各个变量的范围，尽量减少循环数

A的范围：

因为A最小值为1，D最大值为n，且AD=9*t+k；

则A的取值范围：[1,n-9*t-1]

D的范围：

因为AD=9*t+k，且A最小值为1，D最大值为n；

则D的取值范围：[9*t+2,n]

t的范围：

因为D最大为n，且D=A+9*t+1，A最小值为1；

则如果要是有D满足条件，则t满足9*t+2<=n，解得t<n/9；

则t的取值范围：[1,n/9)（此处避免除法，可写作t*9<n）

准备条件妥当，现在还有一个大难题摆在我们面前：如何计算答案？

再分析一下条件：在t一定，且取值范围条件均可满足时，只要满足c-b>6*t，就一定存在四元组，而且只要是满足该条件的所有a,b,c,d，均是四元组。那么若已知该状态下a,b的最大值，那么小于最大值的所有a,b均可形成一个四元组，随着t增大，a,b的最大值相应增大，这时将上个t值时四元组的个数传递下来进行处理，枚举完得到的便是答案。所以，我们可以开四个前缀和数组维护答案。

终焉の代码

分析到这里，也该谈谈代码实现了：

第一层循环：枚举t

没啥好说的。。。

第二层循环：

1.枚举a

枚举a来推b，c，d时，b在a一定的情况下相当于也是定值，那么处理的应是c，d的前缀和，因为c，d均是最大值固定，最小值移动的变量，因此c，d其实要处理的是后缀和，不过我们用倒着枚举a的方式就可以方便地处理后缀和。

for(int A=n-9*t-1;A;A--)
{int B=A+2*t;int D=A+9*t+1;int C=D-t;tem+=sum[C]*sum[D];ans[A][0]+=sum[B]*tem;ans[B][1]+=sum[A]*tem;
}

2.枚举d

与上面同理，只不过因为a,b是最小值固定，最大值移动的变量，所以是正着枚举。

for(int D=9*t+2;D<=n;++D)
{int A=D-9*t-1;int B=A+2*t;int C=D-t;tem+=sum[A]*sum[B];ans[C][2]+=sum[D]*tem;ans[D][3]+=sum[C]*tem;
}

核心代码已经展出，下面是总代码：

/* 1.x[a] < x[b] < x[c]2.x[b] - x[a] = 2 * (x[d] - x[c])3.x[b] - x[a] < (x[c] - x[b]) / 3.0Assumption: t = x[d] - x[c];then: x[b] - x[a] = 2 * t;then: x[c] - x[b] > 6 * t;Assumption: x[c] - x[b] = 6 * t + kso:A -> B: 2 * t;B -> C: 6 * t + k;C -> D: t;so:Range of t: from 1 to n / 9(unequal) Range of A: from 1 to n - 9 * t - 1;Range of D: from 9 * t + 1 + 1 to n;推出以上式子后，枚举t值，便可表示出ABCD的魔法值；再分别枚举A和D，利用乘法原理，算出每个魔法值作为ABCD的次数 
*/
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[40010];
int sum[15010];
int ans[15010][4];
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;++i){scanf("%d",&a[i]);sum[a[i]]++;}for(int t=1;t*9<n;++t){int tem=0;for(int D=9*t+2;D<=n;++D){int A=D-9*t-1;int B=A+2*t;int C=D-t;tem+=sum[A]*sum[B];ans[C][2]+=sum[D]*tem;ans[D][3]+=sum[C]*tem;}tem=0;for(int A=n-9*t-1;A;A--){int B=A+2*t;int D=A+9*t+1;int C=D-t;tem+=sum[C]*sum[D];ans[A][0]+=sum[B]*tem;ans[B][1]+=sum[A]*tem;}}for(int i=1;i<=m;++i){printf("%d %d %d %d\n",ans[a[i]][0],ans[a[i]][1],ans[a[i]][2],ans[a[i]][3]);}return 0;
}

时间复杂度：差不多O（n）~~（我真不会算）~~

后记：

1.帮不是很懂为什么要乘tem的童鞋解释一下：乘法原理_百度百科

2. 如果文章中有地方与代码有出入，请以代码为准，~~毕竟程序一定不会骗人~~