一、简介
git作为应用广泛的一种分布式版本控制系统,其与svn比较最大的差别就是一个是分布式,一个是集中式,git在每个开发者的本地有一个完整的版本库,当在本地处理工作时,无需联网便可修改提交,当需要与其它开发者交互时,只需要提交自己的修改给对方,无需担心集中服务器数据丢失导致所有数据丢失的问题。
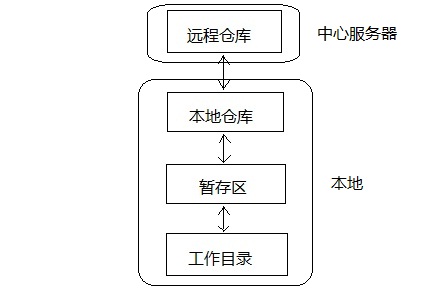
git主要分为工作区、暂存区、本地版本库以及远程版本库,我们平时需要做的也就是将修改更新内容从工作区提交至本地版本库或者推送到远程版本库。
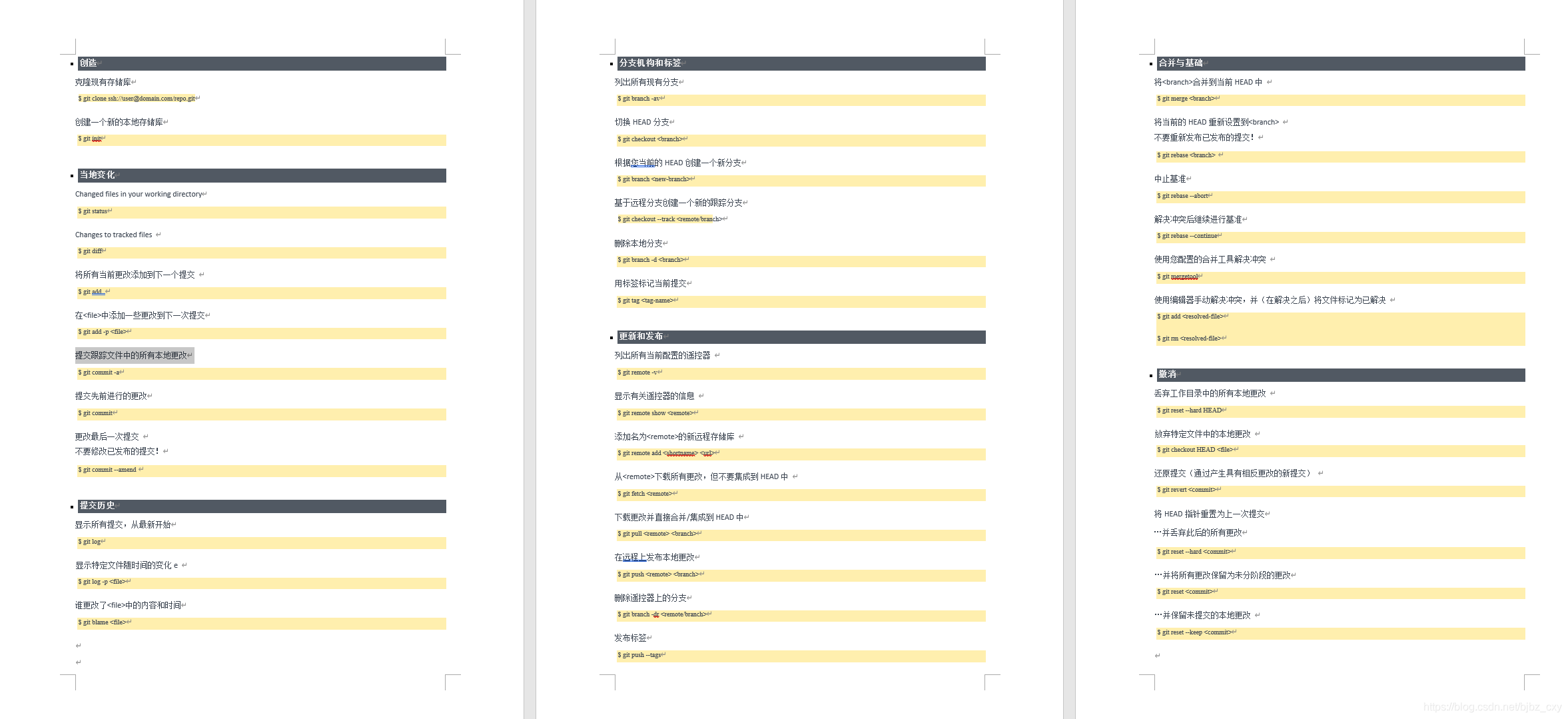
二、常用命令
git init (创建目录后初始化当前仓库)
git clone (将远程仓库克隆至本地,克隆的仓库无需init初始化仓库)
git add (将修改从本地工作区添加至暂存区)
git add .(提交所有修改至暂存区,但不包括删除的文件)
git add --all (提交所有修改至暂存区,包括删除的文件)
git add <filename> (提交某一个文件的修改至暂存区)
git commit(将修改从暂存区提交至本地版本库)
git commit -m (-m后加注释,注释此次提交内容)
git commit --amend (提交了得注释内容需要修改时,此参数可以修改提交的注释内容)
git push (将本地版本库推送至远程仓库)
git pull (拉取远程仓库中内容至本地版本库)
git reset(回退至某个版本)
git reset --hard <commit-id> (根据commit-id回退至某个特定版本,每次提交都会生成一个commit-id,可通过git log命令查看)
git reset --hard HEAD^(回退至上一个版本)
git reset --hard HEAD^^(回退至上两个版本)
git reset --hard HEAD~100(回退至前100个版本)
git checkout -- filename (回退某个文件的修改,checkout命令一般用来切换分支,后面跟-- filename用来回退某个文件的修改)
git branch(创建分支,默认有master主分支)
git checkout (切换分支)
git checkout -b (创建并切换至新建的分支下,该命令=git branch + git checkout)
git branch -a (查看所有分支)
git branch -D (删除分支)
git branch -m oldbranchname newbranchname (修改分支名字)
git merge <branch name> (合并某个分支,譬如合并test分支至master分支,需要先切换至master分支下,然后执行git merge test,将test分支合并至master,不能在将被合并的分支下执行该合并命令)
git stash (保存修改,当有另外的任务需要处理,而正在进行的任务未完成时,可以使用此命令保存修改,会自动创建一个缓存的list集合,方便管理)
git stash list (查看缓存的修改l内容list集合)
git stash pop(将缓存的修改内容释放出来)
git stash apply (将缓存的修改内容释放出来)
git stash apply与git stash pop功能类似,两者的区别是:git stash apply将修改的内容从缓存list中释放出来后,list记录仍然存在,而git stash pop释放缓存内容后,list记录被删除。git stash pop = git stash apply+git stash drop
git log (查看提交修改日志)
git reflog (查看提交修改的日志)
git log与git reflog最大的区别就是能否查看到删除或reset的操作记录,reflog可以看到,而log不行
git diff (查看比较某文件修改内容,不同之处)
git status (查看当前仓库状态,是否有未提交的修改)
git rebase(对最近某一阶段的提交历史进行编辑、删除、复制、粘贴、合并等)
1、当连续多次提交后(git commit提交至本地版本库的操作),譬如提交1、提交2、提交3、提交4,但是你发现其中提交2出现错误需要删除,而又想保留提交3和提交4的内容,这时候就没办法通过reset来回退,这时候就需要用到git rebase;又或者你需要将多次提交合并为一次提交,也需要用到git rebase
git rebase -i HEAD~n (合并前n次的提交记录,并做处理)
上述命令输入后进入编辑界面,参数介绍如下:
pick:保留该commit(缩写:p)
reword:保留该commit,但我需要修改该commit的注释(缩写:r)
edit:保留该commit, 但我要停下来修改该提交(不仅仅修改注释)(缩写:e)
squash:将该commit和前一个commit合并(缩写:s)
fixup:将该commit和前一个commit合并,但我不要保留该提交的注释信息(缩写:f)
exec:执行shell命令(缩写:x)
drop:丢弃该commit(缩写:d)