b站 视频讲解 ： https://www.bilibili.com/video/BV1wh411E7j9/

---

1. 最近邻插值

举个简单例子：一个$3\times 3$ 的单通道图像，如下

如果想把该图像放大为 $4\times 4$大小的图像，那么该怎么做呢？
那么第一步肯定想到的是先把4X4的矩阵先画出来再说，然后，矩阵的每个像素都是未知数，等待着我们去填充：

目标图像的像素值从哪里来来呢？当然是从原图中来，好，先填写目标图最左上角坐标为（0，0）的像素，，那么该坐标 对应 原图中的坐标可以由如下公式得出：

• $srcX=dstX\ast (src\_width/dst\_width)$
• $srcY=dstY\ast (src\_height/dst\_height)$

好了，套用公式，就可以找到对应的原图的坐标了
$(0\ast (3/4),0\ast (3/4))\to (0\ast 0.75,0\ast 0.75)\to (0,0)$

找到了源图的对应坐标,就可以把源图中坐标为 (0,0) 处的像素值 234 填进去 目标图的(0,0)这个位置了。

接下来,如法炮制, 寻找目标图中坐标为 (1,0) 的象素对应源图中的坐标,套用公式:
$(1\ast 0.75,0\ast 0.75)\to (0.75,0)$

结果发现,得到的坐标里面竟然有小数,这可怎么办? 计算机里的图像可是数字图像,象素就是最小单位了,象素的坐标都是整数,从来没有小数坐标。这时候采用的一种策略就是采用四舍五入的方法（也可以采用直接舍掉小数位的方法），把非整数坐标转换成整数。这里按照四舍五入的方法就得到坐标（1，0），完整的运算过程就是这样的：
$(1\ast 0.75,0\ast 0.75)\to (0.75,0)\to (1,0)$
那么就可以再填一个象素到目标矩阵中了，同样是把源图中坐标为(1,0)处的像素值38填入目标图中的(1, 0) 位置。

依次填完每个象素，一幅放大后的图像就诞生：

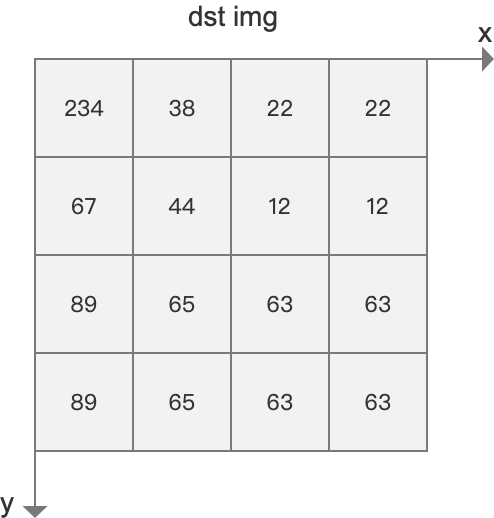
这种放大图像的方法叫做最临近插值算法，这是一种最基本、最简单的图像缩放算法，效果也是最不好的，放大后的图像有很严重的马赛克，缩小后的图像有很严重的失真；效果不好的根源就是其简单的最临近插值方法引入了严重的图像失真，比如，当由目标图的坐标反推得到的源图的的坐标是一个浮点数的时候，采用了四舍五入的方法，直接采用了和这个浮点数最接近的象素的值，这种方法是很不科学的，当推得坐标值为 0.75的时候，不应该就简单的取为1，既然是0.75，比1要小0.25 ，比0要大0.75 ,那么目标象素值其实应该根据这个原图中虚拟的点四周的四个真实的点来按照一定的规律计算出来的，这样才能达到更好的缩放效果。双线型内插值算法就是一种比较好的图像缩放算法，它充分的利用了原图中虚拟点四周的四个真实存在的像素值来共同决定目标图中的一个像素值，因此缩放效果比简单的最邻近插值要好很多。

---

2. 双线性插值

根据于待求点P最近4个点的像素值，计算出P点的像素值。

1）简单理解

对于一个 目标像素，设置坐标通过反向变换得到的浮点坐标为 $(i+u,j+v)$ (其中$i、j$均为浮点坐标的整数部分，$u、v$ 为浮点坐标的小数部分，是取值 [0,1) 区间的浮点数，则这个像素的值 $f(i+u,j+v)$ 可由原图像中坐标为 $(i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)$所对应的周围四个像素的值决定，即：

$$f(i+u,j+v)=(1-u)(1-v)f(i,j)+(1-u)vf(i,j+1)+u(1-v)f(i+1,j)+uvf(i+1,j+1)$$

其中 $f(i,j)$ 表示源图像 $(i,j)$ 处的的像素值，以此类推。

2）一般性

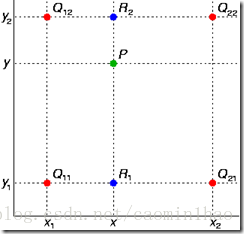
如上图，已知Q12，Q22，Q11，Q21，但是要插值的点为P点，这就要用双线性插值了，首先在x轴方向上，对R1和R2两个点进行插值，这个很简单，然后根据R1和R2对P点进行插值，这就是所谓的双线性插值。说明：下式中$f(\ast )为\ast$点处像素值。

首先在 x 方向进行线性插值，得到：

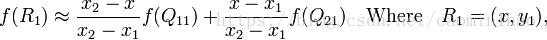
然后在 y 方向进行线性插值，得到：

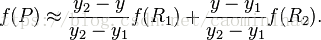
也即点P处像素值：

---

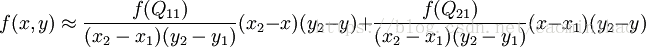
3. 双三次插值（三次样条插值）

假设源图像A大小为mn，缩放K倍后的目标图像B的大小为MN，即K=M/m。A的每一个像素点是已知的，B是未知的，我们想要求出目标图像B中每一像素点(X,Y)的值，必须先找出像素(X,Y)在源图像A中对应的像素(x,y)，再根据源图像A距离像素(x,y)最近的16个像素点作为计算目标图像B(X,Y)处像素值的参数，利用BiCubic基函数求出16个像素点的权重，图B像素(x,y)的值就等于16个像素点的加权叠加。

根据比例关系x/X=m/M=1/K，我们可以得到B(X,Y)在A上的对应坐标为A(x,y)=A(X*(m/M),Y*(n/N))=A(X/K,Y/K)。如图所示P点就是目标图像B在(X,Y)处对应于源图像A中的位置，P的坐标位置会出现小数部分，所以我们假设 P的坐标为P(x+u,y+v)，其中x,y分别表示整数部分，u,v分别表示小数部分（蓝点到a11方格中红点的距离）。那么我们就可以得到如图所示的最近16个像素的位置，在这里用a(i,j)(i,j=0,1,2,3)来表示，如上图。

我们要做的就是求出BiCubic函数中的参数x,从而获得上面所说的16个像素所对应的权重W(x)。BiCubic基函数是一维的，而像素是二维的，所以我们将像素点的行与列分开计算。BiCubic函数中的参数x表示该像素点到P点的距离，例如a00距离P(x+u,y+v)的距离为(1+u,1+v)，因此a00的横坐标权重i_0=W(1+u)，纵坐标权重j_0=W(1+v)，a00对B(X,Y)的贡献值为：（a00像素值）* i_0* j_0。因此，a0X的横坐标权重分别为W(1+u)，W(u)，W(1-u)，W(2-u)；ay0的纵坐标权重分别为W(1+v)，W(v)，W(1-v)，W(2-v)；B(X,Y)像素值为：

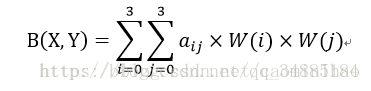
对待插值的像素点(x,y)（x和y可以为浮点数），取其附近的4x4邻域点(xi,yj), i,j = 0,1,2,3。按如下公式进行插值计算：

---

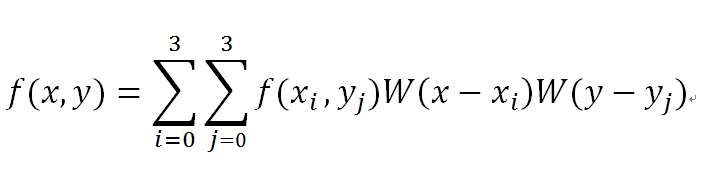
总结

1. 最邻近插值：根据比例关系，得到目标像素 映射在 原图中的浮点像素坐标位置(小数表示)，四舍五入，直接取值。

2. 双线性插值：根据比例关系，得到目标像素 映射在 原图中的浮点像素坐标位置(小数表示)，再利用双线性插值计算出目标像素点的像素值，其根据周围四个像素值和距离位置（小数表示的位置比例）关系得出。

3. 双三次插值 （三次样条插值）：根据比例关系，得到目标像素 映射在 原图中的浮点像素坐标位置(小数表示)，取周围4x4=16个像素，根据位置关系(距离远近)计算出权重(这里有点像高斯滤波，只是不是用高斯公式计算权重)。最后把周围16个像素值算加权和，得出目标像素的像素值。