人工智能之搜索方法

人工智能课程复习笔记专题
人工智能绪论
人工智能之知识表示
人工智能之搜索方法
人工智能之经典逻辑推理
人工智能之专家系统
人工智能之不确定推理方法
人工智能之机器学习

一、搜索的基本概念

1、搜索的含义

根据问题实际情况，不断寻找可利用的知识，构造一条代价最小的推理路线，使问题得以解决的过程称为搜索。

搜索类型
按是否使用启发式信息：盲目搜索、启发式搜索
按问题的表示方式：状态空间搜索、与或树搜索

2、问题表示法

2.1状态空间表示法

状态空间表示法用“状态”和“算符”来表示问题

状态：描述问题求解过程不同时刻的状态
算符：表示对状态的操作
状态空间：由初始状态集合，算符集合、目标状态集合构成的三元组。
状态空间图：状态空间的图表示，节点为状态、有向边为算符
解：初始状态到目标状态所使用的算符序列

例子：二阶“梵塔”问题状态空间方法
1)状态的表示
柱的编号用i,j来代表 (i,j)表示问题的状态其中: i代表A所在的柱子
j 代表B所在的柱子
状态集合 (9种可能的状态)s0=(1,1), s1=(1,2), s2=(1,3)s3=(2,1), s4=(2,2), s5=(2,3)s6=(3,1), s7=(3,2), s8=(3,3)

2)操作（算符）的定义
定义操作A(i,j)表示把A从i移到j；B(i,j)表示把B从i移到j。
操作集合(共12个算符）：
A(1,2),A(1,3),A(2,1),A(2,3),A(3,1),A(3,2)
B(1,2),B(1,3),B(2,1),B(2,3),B(3,1),B(3,2)

3）状态空间图

2.1与或树表示法

与或树表示方法也称问题归约方法。
把复杂问题转换为若干个需要处理的子问题后再加以分别求解的策略，可以递归的进行，直到问题转换为本原问题的集合。

分解
将问题归约为一组子问题，当子问题都有解，原问题才有解。
即子问题的“与”同原问题等价

等价变换
将原问题归约为一组子问题，当子问题其中一个有解，原问题就有解。
即子问题的“或”同原问题等价

本原问题
不能再分解或变换，而且可以直接求解的问题。

端节点与终止节点
在与/或树中，没有子节点的节点称为端节点；若该端节点是本原问题，则为终止节点。

可解节点
满足一下条件之一：
1）它是一个终止节点
2）它是一个或节点，且其子节点至少有一个是可解节点。
3）它是一个与节点，且其子节点均为可解节点

不可解节点
可解节点的条件均不满足

解树
可推出初始节点为可解节点的所有可解节点构成的子树

例子

二、状态空间树的搜索方法

1、状态空间的盲目搜索方法

特点
1）按规定路线搜索，不使用启发式信息
2）适用于状态空间图为树结构的问题
搜索过程
OPEN表：待考查节点
CLOSED表：已考察节点
结束标志
目标状态出现

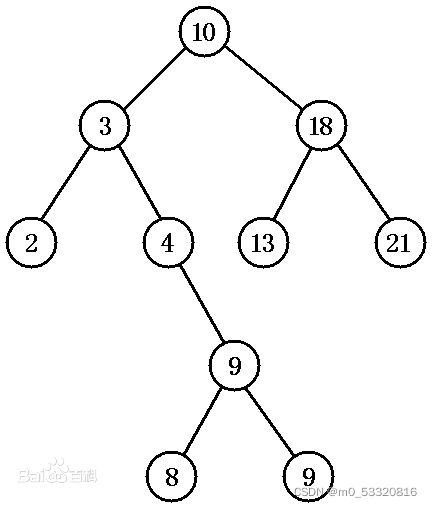
1.1宽度优先搜索

1）把起始节点放入OPEN表中
2）若OPEN表为空表则没有解，失败退出，否则继续。
3）把OPEN表的第一节点N放入CLOSED表中
4）考察节点N是否为目标节点，如果是则得到了解，否则继续
5）如果N不可扩展，转至2），否则继续。
6）取出N的所有节点放入OPEN表末尾，并为其配置父节点指针，然后转至2）

例子

宽度优先改进
判断其子节点是否为目标节点，这样可以减少一层

1.2深度优先搜索

与宽度优先方法相同，只是第3）步从OPEN表取的是最后一个节点。

例子

有界深度优先搜索
固定深度：
到一定深度没有则搜索兄弟节点
可变深度：
先小深度，再变大
可变深度改进：
搜到解后该深度为最大深度，继续搜索，深度只能减小，直至找到最优解

1.3代价树

边上标有代价的树称为代价树。在代价树中，若用g(x)表示从初始节点S0到节点x的代价，用c(x1,x2)表示从父节点x1到子节点x2的代价，则有：
g(x2) = g(x1) + c(x1,x2)

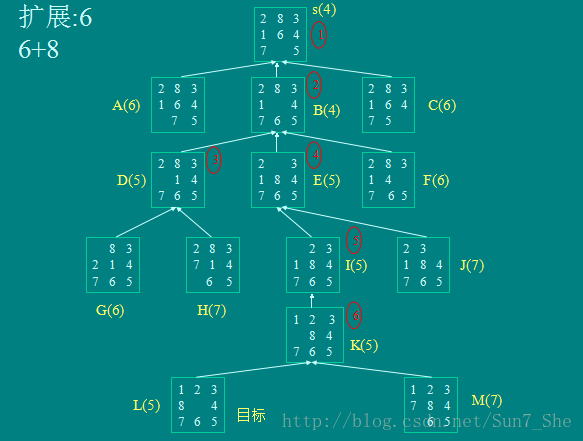
代价树的宽度优先搜索
每次扩展时总是从OPEN表中选取全部代价最小的节点进行扩展。
代价树的深度优先搜索
每次扩展时总是选取刚扩展出来的节点中代价最小的节点进行扩展。

2、状态空间的启发式搜索

在搜索过程中，关键的一步是如何确定下一个要考察的节点，确定的方法不同就形成了不同的搜索策略。如果在确定节点时能充分利用与问题求解有关的控制信息，估计出节点的重要性，就能在搜索时选择重要性较高的节点，以利于求得最优解。

估计函数
f(x) = g(x) + h(x)
其中g(x)为从初始节点S0到节点x已经实际付出的代价；h(x)是从节点x到目标节点Sg的最优路径的估计代价， h(x)称为启发函数，它体现了问题的启发性信息。

局部择优搜索
当一个节点被扩展以后，按f(x)对每一个子节点计算估价值，并选择最小者作为下一个要考察的节点。

深度优先搜索：f(x) = d(x)
代价树的深度优先搜索：f(x) = g(x)
局部择优搜索：f(x) = g(x) + h(x)

全局择优搜索
每次总是从OPEN表的全体节点中选择一个估价值最小的节点。

宽度优先搜索：f(x) = d(x)
代价树的宽度优先搜索：f(x) = g(x)
全局择优搜索：f(x) = g(x) + h(x)

有序搜索

当搜索过程生成一个节点i时，需要把节点i的状态与已生成的所有节点的状态进行比较，若节点i是一个已生成的节点，则表示找到一条通过节点i的新路径。若新路径使节点i的估价值更小，则修改节点i指向父节点的指针，使之指向新的父节点；否则，不修改节点i原有的父节点指针，即保留节点i原有的路径。

(1) 把初始节点S0放入OPEN表，f(S0)。
(2) 如果OPEN表为空，则问题无解，退出。
(3) 把OPEN表的第一个节点(记为节点n)取出放入CLOSED表。
(4) 考察节点n是否为目标节点。若是，则求得了问题的解，退出。
(5) 若节点n不可扩展，则转第(2)步。
(6) 扩展节点n，生成其全部子节点。对节点n的每个子节点i，计算f(i)。考察节点i是否为已生成过的节点。① 如果节点i既不在OPEN表中，又不在CLOSED表中，则节点  i是一个新节点。为节点i配置指向父节点n的指针，把节点I 放入OPEN表中，然后对OPEN表中的全部节点按估价值从小到大的顺序进行排序。② 如果节点i已在OPEN表中或在CLOSED表中，则节点i是一个已生成过的节点。比较节点i刚计算的f(i)新值与表中记载的 f(i)旧值，若新的f(i)值较小则：(a)对表中节点i的有关记载进行下述修改：用f(i)的新值代替旧值，修改节点i指向父节点的指针，使之指向新的父节点n。(b)若节点i在CLOSED表中，则把节点i移回OPEN表。(7) 然后转第(2)步

A*算法

我们希望估价函数f是f*的一个估计，此估计可由下式给出：　　　　f(n)=g(n)+h(n)　　其中：g是g*的估计；h是h*的估计。对于g(n)来说。很显然g(n)≥g*(n)。对于h*(n)估计h(n)，它依赖于有关问题的领域的启发信息。

定义1 ：在GRAPHSEARCH过程中，如果第8步的重排OPEN表是依据f(x)=g(x)+h(x)进行的，则称该过程为A算法。
定义2 ：在A算法中，如果对所有的x，h(x)≤h*(x)成立,则称h(x)为h*(x)的下界，它表示某种偏于保守的估计。
定义3 ：采用h*(x)的下界h(x)为启发函数的A算法，称为A*算法。　　

三、与或树的搜索算法

基本思想：
扩展（自上而下）
标示（自下而上）
结束条件：初始节点为可解或不可解

搜索过程：
（1）把原始问题作为初始节点S0,并将其作为当前节点。
（2）应用分解或等价变换算符对当前节点进行扩展。
（3）为每个子节点设置指向父节点的指针
（4）选择合适的子节点作为当前节点,反复应用（2）（3）步，在此期间要多次应用可解标示过程和不可解标示过程，直到初始节点被标示为可解节点或不可解节点。
可解标示过程：
由可解子节点来确定父节点，祖父节点等为可解节点的过程
‘与’节点只有当其子节点全为可解节点时，才为可解节点；
‘或’节点只要有一个子节点为可解节点，它就是可解节点。
不可解标示过程：
由不可解子节点来确定父节点，祖父节点等为不可解节点的过程
‘与’节点只要其子节点有一个为不可解节点，它就是不可解节点；
‘或’节点只有当其子节点都为不可解节点，它才是不可解节点。