熵编码（算术+霍夫曼）编解码基础知识总结

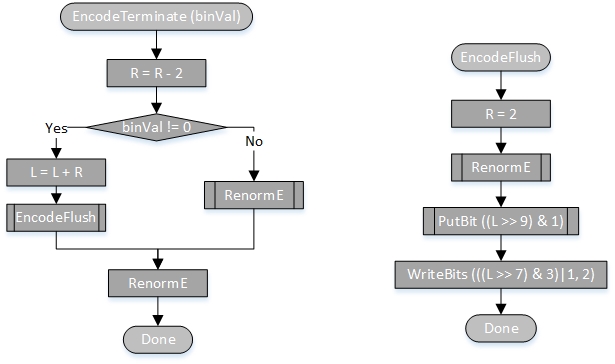
在MPEG的TMC13模型中，对于surface point cloud compression，对block和vertices进行熵编码；对于lidar point cloud compression，需要对量化残差进行算术编码。这里对熵编码相关的知识进行了总结。

熵编码:

(1)https://blog.csdn.net/m0_37579288/article/details/79552526 (2)https://zhuanlan.zhihu.com/p/26454072

信息论中，Shannon发明了信息熵，信息熵是信息量的度量单位，信息学里的熵表示数据的无序度，熵越高，则包含的信息越多。

熵编码是一种无损编码方式。最常见熵编码有霍夫曼(Huffman)编码，算术编码，还有行程编码 (RLE)、基于上下文的自适应变长编码(CAVLC)、基于上下文的自适应二进制算术编码(CABAC)。

在图像（视频）压缩和点云压缩中经常用到熵编码，譬如，JPEG用的是Huffman和算术编码，而CAVLC、CABAC是HEVC中使用的两种编码方式。

算术编码：

原理解析：https://blog.csdn.net/u010029439/article/details/104147157

模拟算数编码步骤：https://blog.csdn.net/lkxiaolou/article/details/8781024

算数编码实验：https://blog.csdn.net/CSDNJay/article/details/46628603 MATLAB代码

算术编码和其他熵编码方式的不同在于，其他的熵编码通常是把输入的消息分割为符号，对每个符号进行编码，而算术编码是直接吧整个输入的消息编码为一个数，小数介于 [ 0.0 , 1.0 ) 区间。其大体过程为：

假设有一段数据需要编码，统计里面所有的字符和出现的次数。
将区间 [0,1) 连续划分成多个子区间，每个子区间代表一个上述字符，区间的大小正比于这个字符在文中出现的概率 p。概率越大，则区间越大。所有的子区间加起来正好是 [0,1)。
编码从一个初始区间 [0,1) 开始，设置:，
不断读入原始数据的字符，找到这个字符所在的区间，比如 [ L, H )，更新:
最后将得到的区间 [low, high)中任意一个小数以二进制形式输出即得到编码的数据。

举例说明：

（1）有一段原始数据“ARBER”，他们出现的概率和次数如下：

Symbol	Times	P
A	1	0.2
B	1	0.2
E	1	0.2
R	2	0.4

（2）将这几个字符的区间在 [0，1) 上按照概率大小连续一字排开，我们得到一个划分好的 [0，1)区间：
图片描述

（3）开始编码，初始区间是 [0，1)。注意这里又用了区间这个词，不过这个区间不同于上面代表各个字符的概率区间 [0，1)。这里我们可以称之为编码区间，这个区间是会变化的，确切来说是不断变小。我们将编码过程用下图完整地表示出来：
图片描述

可以看出编码区间逐渐变小。每次编码一个字符，就在现有的编码区间上，按照概率比例取出这个字符对应的子区间。例如一开始A落在0到0.2上，因此编码区间缩小为 [0，0.2)，第二个字符是R，则在 [0，0.2)上按比例取出R对应的子区间 [0.12，0.2)，以此类推。每次得到的新的区间都能精确无误地确定当前字符，并且保留了之前所有字符的信息，因为新的编码区间永远是在之前的子区间。最后我们会得到一个长长的小数，这个小数神奇地包含了所有的原始数据，不得不说这真是一种非常精彩的思想。

（4）解码：如果你理解了编码的原理，则解码的方法显而易见，就是编码过程的逆推。从编码得到的小数开始，不断地寻找小数落在了哪个概率区间，就能将原来的字符一个个地找出来。例如得到的小数是0.14432，则第一个字符显然是A，因为它落在了 [0，0.2)上，接下来再看0.14432落在了 [0，0.2)区间的哪一个相对子区间，发现是 [0.6，1)，就能找到第二个字符是R，依此类推。在这里就不赘述解码的具体步骤了。

代码：MATLAB

https://www.zhihu.com/question/32301828 介绍function cumsum()

涉及的MATLAB函数：cumsum() find() vpa()

%%算术编码
clc; 
a=['_','a','e','r','s','t']; 
s=input('字符串'); 
space=0;a1=0;e1=0;r1=0;s1=0;t1=0; 
for i=1:length(s)c=find(a==s(i));switch c case 1 space=space+1; case 2 a1=a1+1; case 3 e1=e1+1; case 4r1=r1+1; case 5s1=s1+1;case 6t1=t1+1;end 
end
disp('_,a,e,r,s,t概率分别是');
p=[space,a1,e1,r1,s1,t1]/length(s) 
sp=cumsum(p);  %cumsum累计求和，sp=a1,a1+a2,a1+a2+a3,...
low=0;high=1;
range_length=high-low; 
for i=1:length(s) c=find(a==s(i)); %find函数用来定位High=sp(c);Low=High-p(c);next_low=low+range_length*Low; next_high=low+range_length*High;low=next_low;high=next_high;range_length=high-low; disp([vpa(low,11),vpa(high,11)]) %vpa用于精度控制
end

在命令行窗口输入‘state_tree’，（注意加单引号），结果如下：

clc;
format long
p=[0.1,0.1,0.3,0.1,0.1,0.3];
s='_aerst';
high=cumsum(p);
low=high-p;
number=input('输入数值');
while(number)c=find((number>=low)&(number<high));disp(s(c));range_low=low(c);range=p(c);number_next=vpa(((number-range_low)/range),11);number=double(number_next);
end

输出是state_treatttt.....由于取了精度，最后的结果会有误差。

霍夫曼编码：

（1）https://www.cnblogs.com/Jezze/archive/2011/12/23/2299884.html 哈夫曼编码与哈夫曼树

（2）https://blog.csdn.net/u014106644/article/details/90050977 霍夫曼编码原理和Java代码

（3）https://blog.csdn.net/xgf415/article/details/52628073 霍夫曼编码很详细的步骤，好评鸭

霍夫曼编码的具体步骤如下：

将信源符号的概率按减小的顺序排队。
把两个最小的概率相加，并继续这一步骤，始终将较高的概率分支放在右边，直到最后变成概率１。
画出由概率１处到每个信源符号的路径，顺序记下沿路径的０和１，所得就是该符号的霍夫曼码字。
将每对组合的左边一个指定为0，右边一个指定为1（或相反）。

例如给定一段数据，统计里面字符的出现次数，生成哈夫曼树，我们可以得到字符编码集：

Symbol	Times	Encoding
a	3	00
b	3	01
c	2	10
d	1	110
e	2	111

图片描述

仔细观察编码所表示的小数，从0.0到0.111，其实就是构成了算数编码中的各个概率区间，并且概率越大，所用的bit数越少，区间则反而越大。概率越小的字符，用更多的bit去表示，这反映到概率区间上就是，概率小的字符所对应的区间也小，因此这个区间的上下边际值的差值越小，为了唯一确定当前这个区间，则需要更多的数字去表示它。我们仍以十进制来说明，例如大区间0.2到0.3，我们需要0.2来确定，一位足以表示；但如果是小的区间0.11112到0.11113，则需要0.11112才能确定这个区间，编码时就需要5位才能将这个字符确定。

哈夫曼编码的不同之处就在于，它所划分出来的子区间并不是严格按照概率的大小等比例划分的（节点的左右子树按照0.5/0.5的概率划分）。例如上面的d和e，概率其实是不同的，但却得到了相同的子区间大小0.125。可以将哈夫曼编码和算术编码在这个例子里的概率区间做个对比：

图片描述

代码：C语言

#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>#define MAXBIT      100
#define MAXVALUE  10000
#define MAXLEAF     30
#define MAXNODE    MAXLEAF*2 -1typedef struct
{int bit[MAXBIT];int start;
} HCodeType;        /* 编码结构体 */typedef struct
{int weight;int parent;int lchild;int rchild;char value;
} HNodeType;        /* 结点结构体 *//* 构造一颗哈夫曼树 */
void HuffmanTree(HNodeType HuffNode[MAXNODE], int n)
{/* i、j： 循环变量，m1、m2：构造哈夫曼树不同过程中两个最小权值结点的权值，x1、x2：构造哈夫曼树不同过程中两个最小权值结点在数组中的序号。*/int i, j, m1, m2, x1, x2;/* 初始化存放哈夫曼树数组 HuffNode[] 中的结点 */for (i = 0; i < 2 * n - 1; i++){HuffNode[i].weight = 0;//权值 HuffNode[i].parent = -1;HuffNode[i].lchild = -1;HuffNode[i].rchild = -1;HuffNode[i].value = ' '; //实际值，可根据情况替换为字母  } /* end for *//* 输入 n 个叶子结点的权值 */for (i = 0; i < n; i++){printf("Please input char of leaf node: ", i);scanf("%c", &HuffNode[i].value);getchar();} /* end for */for (i = 0; i < n; i++){printf("Please input  weight of leaf node: ", i);scanf("%d", &HuffNode[i].weight);getchar();} /* end for *//* 构循环造 Huffman 树 */for (i = 0; i < n - 1; i++){m1 = m2 = MAXVALUE;     /* m1、m2中存放两个无父结点且结点权值最小的两个结点 */x1 = x2 = 0;/* 找出所有结点中权值最小、无父结点的两个结点，并合并之为一颗二叉树 */for (j = 0; j < n + i; j++){if (HuffNode[j].weight < m1 && HuffNode[j].parent == -1){m2 = m1;x2 = x1;m1 = HuffNode[j].weight;x1 = j;}else if (HuffNode[j].weight < m2 && HuffNode[j].parent == -1){m2 = HuffNode[j].weight;x2 = j;}} /* end for *//* 设置找到的两个子结点 x1、x2 的父结点信息 */HuffNode[x1].parent = n + i;HuffNode[x2].parent = n + i;HuffNode[n + i].weight = HuffNode[x1].weight + HuffNode[x2].weight;HuffNode[n + i].lchild = x1;HuffNode[n + i].rchild = x2;printf("x1.weight and x2.weight in round %d: %d, %d\n", i + 1, HuffNode[x1].weight, HuffNode[x2].weight);  /* 用于测试 */printf("\n");} /* end for */
} /* end HuffmanTree *///解码 
void decodeing(char string[], HNodeType Buf[], int Num)
{int i, tmp = 0, code[1024];int m = 2 * Num - 1;char *nump;char num[1024];for (i = 0; i < strlen(string); i++){if (string[i] == '0')num[i] = 0;elsenum[i] = 1;}i = 0;nump = &num[0];while (nump < (&num[strlen(string)])){tmp = m - 1;while ((Buf[tmp].lchild != -1) && (Buf[tmp].rchild != -1)){if (*nump == 0){tmp = Buf[tmp].lchild;}else tmp = Buf[tmp].rchild;nump++;}//	printf("123");printf("字符编号是：%d", tmp);printf("%c", Buf[tmp].value);//这里一直显示不出来}
}int main(void)
{HNodeType HuffNode[MAXNODE];            /* 定义一个结点结构体数组 */HCodeType HuffCode[MAXLEAF], cd;       /* 定义一个编码结构体数组， 同时定义一个临时变量来存放求解编码时的信息 */int i, j, c, p, n;char pp[100];printf("Please input n:\n");scanf("%d", &n);HuffmanTree(HuffNode, n);for (i = 0; i < n; i++){cd.start = n - 1;c = i;p = HuffNode[c].parent;while (p != -1)   /* 父结点存在 */{if (HuffNode[p].lchild == c)cd.bit[cd.start] = 0;elsecd.bit[cd.start] = 1;cd.start--;        /* 求编码的低一位 */c = p;p = HuffNode[c].parent;    /* 设置下一循环条件 */} /* end while *//* 保存求出的每个叶结点的哈夫曼编码和编码的起始位 */for (j = cd.start + 1; j < n; j++){HuffCode[i].bit[j] = cd.bit[j];}HuffCode[i].start = cd.start;} /* end for *//* 输出已保存好的所有存在编码的哈夫曼编码 */for (i = 0; i < n; i++){printf("%d 's Huffman code is: ", i);for (j = HuffCode[i].start + 1; j < n; j++){printf("%d", HuffCode[i].bit[j]);}printf(" start:%d", HuffCode[i].start);printf("\n");}printf("Decoding,Please Enter 0/1 code:\n");scanf("%s", &pp);decodeing(pp, HuffNode, n);getchar();return 0;
}

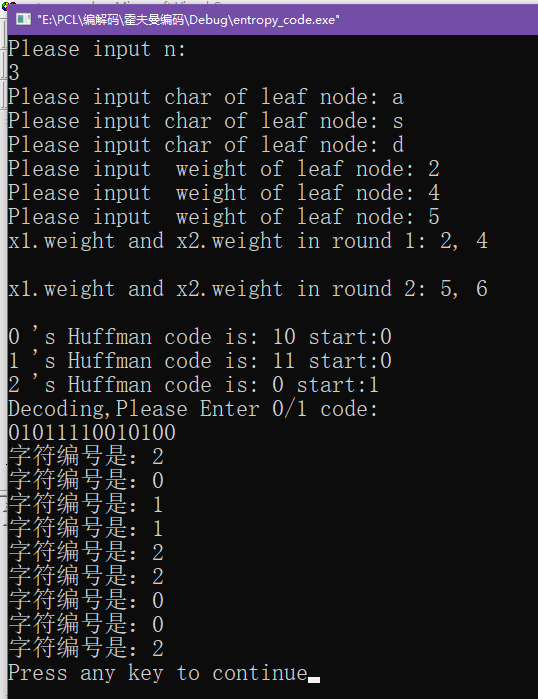
实验结果如下：【疑问】本来是输入0/1编码后，直接输出解码的结果，但解码部分最后一步printf("%c", Buf[tmp].value);不知为何一直显示不了，我看了好久，也不知道哪里有问题，枯了，请各位路过的道友知道怎么改的烦请在评论区纠正一下，谢谢啦~