在压缩算法中,熵编码是其中重要的无损压缩步骤。熵编码算法根据香农定理,对出现概率大的源符号用较少的编码符号进行编码,对概率小的源符号用较多的编码符号进行编码,尽可能地逼近压缩的极限。
目前各类压缩工具使用的熵编码算法主要有Huffman encoding,Arithmetic encoding, Range encoding和新出的Asymmetric Number System这几种算法。其中Huffman encoding由于只能在各个数据出现的概率固定为2的-n次方时才能达到最大,因此对于很多应用场景不适用。在视频编解码中,常用的是Arithmetic encoding和Range encoding,对于任意概率分布的符号流都能达到理论最优而且还适用于马尔可夫过程(概率可变,但只和过去的概率相关,和未来的概率无关)。它们二者本质上是同一种算法,但是对于算法中的概念有着不同的阐释。现实中Arithmetic encoding经常被一些专利保护着,比如CABAC,因此开源项目往往青睐于自行编写Range encoding算法进行熵编码。本文主要介绍Range encoding工程上的原理和实现。
示例步骤格式说明
<执行原因> -> <执行内容1>;<执行内容2>... //注释
基本实现
Range encoding算法持有一个整数Range(范围)作为其自身的状态,并对于每种符号按其概率大小比例对Range划分。编码时对于每一个输入的符号,将当前Range更新为该符号所落入的原Range的划分;在编码的最后当前范围的起始值作为编码结果。解码时检查编码结果,它落在哪个划分中就输出哪个符号,并取该划分为当前Range,不断迭代直至编码结果与当前范围的起始值相等。
举一个例子
令输入符号集合为{A B},概率为60%、40%,初始Range为[0, 10000),源符号流为AAB
则编码算法进行如下步骤:
initial -> range = [0, 10000);
update -> rangeA = [0, 6000); rangeB = [6000, 10000) //A占60%,B占40%
input A -> range = [0, 6000)
update -> rangeA = [0, 3600); rangeB = [3600, 6000)
input A -> range = [0, 3600)
update -> rangeA = [0, 2160); rangeB = [2160, 3600)
input B -> range = [2160, 3600)
update -> rangeA = [2160, 3024); rangeB = [3024, 3600)
end of input -> output 2160; end
如图所示:
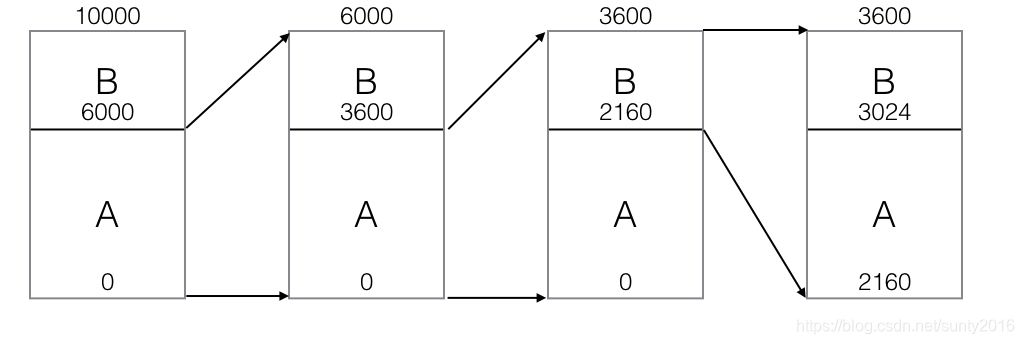
解码算法进行如下步骤,假设输入的编码结果为上例中的2160:
initial -> range = [0, 10000);
update -> rangeA = [0, 6000); rangeB = [6000, 10000)
2160 in rangeA -> range = [0, 6000); output A
update -> rangeA = [0, 3600); rangeB = [3600, 6000)
2160 in rangeA -> range = [0, 3600); output A
update -> rangeA = [0, 2160); rangeB = [2160, 3600)
2160 in rangeB -> range = [2160, 3600); output B
update -> rangeA = [2160, 3024); rangeB = [3024, 3600)-> end
可见解码输出与编码输入相等。
简单的重归一化
从Range encoding的原理中可以看到,算法当前Range是会逐渐缩小的,那么必然会面临随着不断地输入Range变得过小无法提供足够精度来表示概率,最后甚至缩小至0的问题。那么如果想用该算法来编码不限长度的符号流时,一种办法就是使用不限字长的大数对象来存储Range的起止值,并且在每次更新当前Range时检查Range大小,如果小于某个特定值就将起止值乘以相同的数以扩大Range大小。
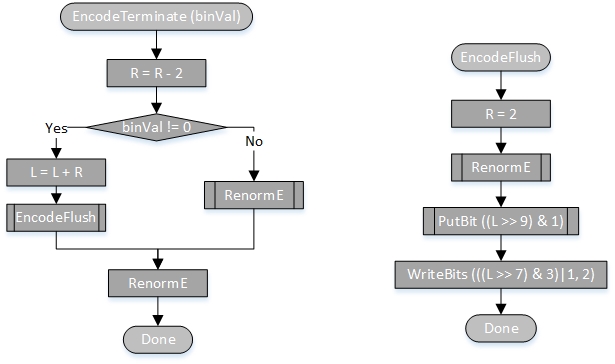
但是这样做也有一个问题,有一些应用(比如直播)希望能够以流的方式处理数据,而无限精度整数对象需要把数据都保存在内存里,无疑是无法满足需求的。因此人们想出一个办法——还是采用固定长度的整数来保存Range起止值,但是在Range需要扩容时,通过移位的方式(对十进制相当于乘以10n,对于二进制相当于乘以2n,n位移位个数),将Range的起止值的高位的数据从整数中移除并送到输出流里去,这样一来就可以保证Range coding的算法能够一直进行下去。这种调整Range大小的过程被称为重归一化。使用了重归一化的算法在编码结束时需要进行一个flush操作,强制将当前未移出的位移出到流里;而在解码开始前则必须先从流里读若干位把定长整数code填满,重归一化时要移除code高位,并从流中输入同样位数进入低位,结束的判断条件为判断输入符号是否全部处理。
为了举例说明这种方法,基于以上节的例子,将概率做些调整:
令输入符号集合为{A B},概率为99%、1%。Range起始寄存器和终止都是4位,其中终止寄存器用0000表示10000,因此初始Range为[0000, 0000)。源符号流为ABA,同时令Range大小必须大于100。
则编码算法进行如下步骤:
initial -> range = [0000, 0000); //终止值用0000表示10000
update -> rangeA = [0000, 9900); rangeB = [9900, 0000)
input A -> range = [0000, 9900)
update -> rangeA = [0000, 9801); rangeB = [9801, 9900)
input B -> range = [9801, 9900)
|range| <= 100 -> range = [0100, 0000); output '98'
update -> rangeA = [0100, 9901); rangeB = [9901, 0000)
input A -> range = [0100, 9901)
flush -> output '0100'; end
编码结束,输出为’980100’。
解码算法进行如下步骤:
initial -> range = [0000, 0000); code = '9801'
update -> rangeA = [0000, 9900); rangeB = [9900, 0000)
code in rangeA -> range = [0000, 9900); output 'A'
update -> rangeA = [0000, 9801); rangeB = [9801, 9900)
code in rangeB -> range = [9801, 9900); output 'B'
|range| <= 100 -> range = [0100, 0000); code = '0100'
update -> rangeA = [0100, 9901); rangeB = [9901, 0000)
code in rangeA -> range = [0100, 9901); output 'A'-> end
解码结束,输出’AAB’。
简单重归一化的问题
现在表面上看起来,已经解决了全部问题,但实际上这里有一个巨大的坑——在刚才的例子里继续输入若干源符号:
令输入符号集合为{A B},概率为99%、1%,Range起始寄存器和终止都是4位,其中终止寄存器用0000表示10000,因此初始Range为[0000, 0000)。源符号流为ABABAB。令Range大小必须大于100。
则编码算法进行如下步骤:
initial -> range = [0000, 0000); //终止值用0000表示10000
update -> rangeA = [0000, 9900); rangeB = [9900, 0000)
input A -> range = [0000, 9900)
update -> rangeA = [0000, 9801); rangeB = [9801, 9900)
input B -> range = [9801, 9900)
|range| <= 100 -> range = [0100, 0000); output '98'
update -> rangeA = [0100, 9901); rangeB = [9901, 0000)
input A -> range = [0100, 9901)
update -> rangeA = [0100, 9803); rangeB = [9803, 9901)
input B -> range = [9803, 9901)
|range| <= 100 -> range = [0300, 0100); output '98'
update -> ???
可以发现当前Range的起始值竟然大于终止值,致使算法无法继续进行下去了。这是怎么回事呢?
再次审视重归一化过程,可以发现重归一化过程其实是把Range所在的空间分成了pn个小块(p为进制数,n为移动位数),然后将最底部的小块扩展pn倍变成原空间大小,而其他小块实际上被丢弃了。
如图所示:

在这个过程中,如果当前Range跨越了两个(或多个)小块,则会出现信息的丢失,因为算法最终收敛的位置可能在被丢失的小块中。在刚才的例子中,p = 10且n = 2,整个空间为[0, 10000),因此每100个整数一个小块。第二次重归一化前的Range[9803, 9901)都跨越了[9800, 9900)和[9900, 10000)两个小块,所以会出错。正确的做法是先不进行重归一化而是让算法继续收敛直到当前Range完全落入同一个小块中。
用修正过重归一化的算法应用于上个例子:
则编码算法进行如下步骤:
initial -> range = [0000, 0000); //终止值用0000表示10000
update -> rangeA = [0000, 9900); rangeB = [9900, 0000)
input A -> range = [0000, 9900)
update -> rangeA = [0000, 9801); rangeB = [9801, 9900)
input B -> range = [9801, 9900)
renormalize -> range = [0100, 0000); output '98'
update -> rangeA = [0100, 9901); rangeB = [9901, 0000)
input A -> range = [0100, 9901)
update -> rangeA = [0100, 9803); rangeB = [9803, 9901)
input B -> range = [9803, 9901)
update -> rangeA = [9803, 9900); rangeB = [9900, 9901) //不满足重归一化条件,继续update
input A -> range = [9803, 9900)
renormalize -> range = [0300, 0000); output '98'
update -> rangeA = [0300, 9903); rangeB = [9903, 0000)
input B -> range = [9903, 0000)
renormalize -> range = [0300, 0000); output '99'
flush -> output '0300'; end
编码结束,输出为’9898990300’。
解码算法进行如下步骤:
initial -> range = [0000, 0000); code = '9898'
update -> rangeA = [0000, 9900); rangeB = [9900, 0000)
code in rangeA -> range = [0000, 9900); output 'A'
update -> rangeA = [0000, 9801); rangeB = [9801, 9900)
code in rangeB -> range = [9801, 9900); output 'B'
renormalize -> range = [0100, 0000); code = '9899'
update -> rangeA = [0100, 9901); rangeB = [9901, 0000)
code in rangeA -> range = [0100, 9901); output 'A'
update -> rangeA = [0100, 9803); rangeB = [9803, 9901)
code in rangeB -> range = [9803, 9901); output 'B'
update -> rangeA = [9803, 9900); rangeB = [9900, 9901) //不满足重归一化条件,继续update
code in rangeA -> range = [9803, 9900); output 'A'
renormalize -> range = [0300, 0000); code = '9903'
update -> rangeA = [0300, 9903); rangeB = [9903, 0000)
code in rangeB -> range = [9903, 0000); output 'B'
renormalize -> range = [0300, 0000); code = '0300'-> end
解码结束,输出’ABABAB’。
这样一来,刚才的问题就解决了。
然而,细心的读者可能又发现了一个问题————如果重归一化的条件一直不满足怎么办呢?会不会又重蹈了Range大小归零的覆辙?回答:是的,虽然不常见但确实有这种可能!一个解决办法是,如果形如[a, a+m)的Range仍然不满足重归一化条件,则起始值照常移位并输出高位,而终止值直接置成整个空间的终止值!Range encoding算法要保证正确性只要保证编码和解码时每一步状态都一致即可。这里新的Range中终点值必须大于起始值,而且要留出足够的精度空间进行之后计算,因此设成空间终点值是合理的做法。
参考代码
上述若干例子使用的都是十进制range,并且只有两个源符号,下面给出任意多个符号的二进制Range encoding伪代码:
/** S为源符号列表* P为源符号概率列表*/
void encode(String[] S, float[] P, Stream input, Stream output) {Range R = new Range(0x0000, 0x0000);Range[] subR = R.partition(S, P);foreach s in input {int index = {i | S[i] == s}R = subR[index];//重归一化while (R.start & 0xFF00) == ((R.end-1) & 0xFF00) {output.write((R.start >> 8) & 0x00FF);R.start = (R.start << 8) & 0xFFFF;R.end = (R.end << 8) & 0xFFFF;}//Range过小强制输出if R.size() <= 0x10 {output.write((R.start >> 8) & 0xFF);R.start = (R.start << 8) & 0xFFFF;R.end = 0x0000;}//更新subR = R.partition(S, P);}//flushoutput.write((R.start >> 8) & 0xFF);output.write(R.start & 0xFF);
}/** S为源符号列表* P为源符号概率列表*/
void decode(String[] S, float[] P, Stream input, Stream output) {Range R = new Range(0x0000, 0x0000);Range[] subR = R.partition(S, P);int C = input.readBits(16);while !output.eos() {int index = {i | subR[i].contains(C)};output.write(S[index]);R = subR[index];//重归一化while (R.start & 0xFF00) == ((R.end-1) & 0xFF00) {R.start = (R.start << 8) & 0xFFFF;R.end = (R.end << 8) & 0xFFFF;C = ((C << 8) | input.readBits(8)) & 0xFFFF;}//Range过小强制输出if R.size() <= 0x10 {R.start = (R.start << 8) & 0xFFFF;R.end = 0x0000;C = ((C << 8) | input.readBits(8)) & 0xFFFF;}//更新subR = R.partition(S, P);}
}
其他
对于Range encoding能够压缩源符号流的直观理解
为什么这种算法能够起到压缩作用?从前面的例子可以看出,只要不执行重归一化,编码过程的输出就永远都是一个固定位数的数字。因此,Range coding算法对出现概率大的符号选取大的范围,就相当于减少了重归一化的执行次数,即熵编码所遵循的用较少的编码符号编码概率较大的源符号的规律。
Arithmetic encoding和Range encoding的关系
Arithmetic encoding把整个范围空间看作[0.0, 1.0),把编码输出看作是[0, 1)间的一个小数,而非像Range encoding这样在整数的空间下进行。但它们实质上是相同的算法。
接下来的问题是:
1)如何使用Range encoding编码比特流
2)如何进行可变概率符号的Range encoding
将在下篇文章中介绍。