前言

信息论是由克劳德·香农发展，用来找出信号处理与通信操作的基本限制，如数据压缩、可靠的存储和数据传输等。自创立以来，已被应用多个领域，例如自然语言处理(NLP)、机器学习等领域。

定长编码(Block Codes)

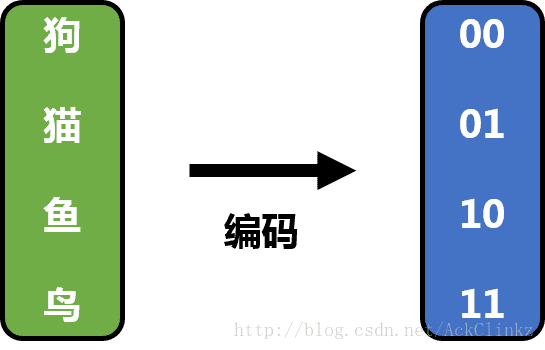
让我们从一个例子开始。小明酷爱动物，日常谈吐中经常提及各种动物，包括：狗、猫、鱼和鸟。一天，小明见到小红（原谅我这么俗的名字），两个人决定用二进制的方式来交流。为了交流方便，小明和小红决定制定一套编码规则

此时，若小明要发出“狗 猫 狗 鸟”的信息，需要完成以下过程：

通过以上三个过程，便可以将“狗 猫 狗 鸟”转化为二进制了。

变长编码(Variable Codes)

实际中，通讯往往需要付费，假设通讯按位（bit）收费。为了省钱，小明和小红需要寻找合适的编码策略。在设计编码策略中，小红统计了小明的说话

此时，若按照上面的定长编码，每个字的平均编码长度

$$L(x)=2\times\frac{1}{2}+2\times\frac{1}{4}+2\times\frac{1}{8}+2\times\frac{1}{8}=2$$

若想进一步压缩平均编码长度，变长编码是一种有效的手段。变长编码的基本思想：出现频率高的字符使用短编码，出现频率低的字符使用长编码。（你可能会问，为什么不让所有的编码都使用短编码？嘿嘿，都使用短编码，还能实现一一对应吗？）基于上述思想，小明和小红重新指定了一套新的编码策略:

此时，每个字的平均编码长度为

$$L(x)=1\times\frac{1}{2}+2\times\frac{1}{4}+3\times\frac{1}{8}+3\times\frac{1}{8}=1.75$$

显然，新的策略能够帮小明和小红省很多钱。那么，小明和小红是如何设计的呢？

无损编码(lossless compression)

为了便于接下来的描述，以下图为例介绍几个名称

其中狗、猫、鱼等称为源符号，$0$、$01$、$110$等称为码字，整个映射使用$C(x)$表示。

无损编码

小明和小红的交流中，首先要保证信息的无损性，即保证编码后的信息能够无损的复原。若使用定长编码，复原信息轻而易举便可实现，而变长编码则不同。假如使用上图,此时小明给出的代号为

根据约定好的码表，小红既可以理解成“狗 狗 鸟 狗”，也可以理解成“狗 猫 鱼”。显然，这是小明和小红不愿意看到的。通过查阅资料，小明和小红发现他们遇到的问题是“无损编码”问题：

无损编码是一类数据压缩算法，其压缩的数据能够无损的复原为原始数据。

若$C(x)$是无损编码，它需要是：

• 非奇异编码（Non-singular code）：$x_1 \neq x_2 \Longrightarrow C(x_1) \neq C(x_2)$

在实际中，我们往往需要一次编码一系列字符，而不是一次编码一个字符，因此它需要满足：

• 可扩展编码（Extension of a code）：$C(x_1,...,x_n)=C(x_1)...C(x_n)$
• 唯一可译解码（Unique decodability）：$x_i^n \neq x_j^m \Longrightarrow C(x_i^n) \neq C(x_j^m)$

尽管唯一可译解码已经足够强了，但它并不能支撑“收到所有字符以后才进行解码”的情况。例如，$C(x)$是

$x$	1	2	3	4
$C(x)$	10	00	11	110

当收到的代号是$110000$，解码为$322$，而收到的代号是$1100000$，解码为422。显然，当收到所有信息再解码时，$11$就表示了不同的字符。对于此种问题，前缀编码是一种有效的解决方案,定义如下：

• $x_1 \neq x_2 \Longrightarrow C(x_1) \neq Prefix(C(x_2))$

即任意符号的编码都不是其他编码的前缀。基于前缀编码，$C(x)$是

$x$	1	2	3	4
$C(x)$	0	10	110	111

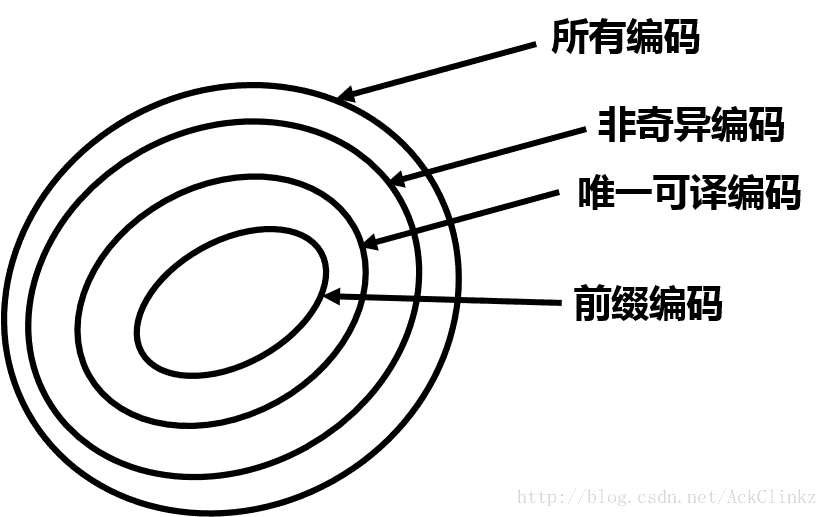
在上面的介绍中，分别介绍了“非奇异编码”、“唯一编码”、“前缀编码”。这些编码方式的相互关系可以通过下图来描述：

通过上面的知识，前缀编码是解决编码复原最好的方式，下面就需要考虑如何优化编码长度。

最优编码

需要注意的是，本文讨论的是源符号有限且已知的编码。更多关于最优编码的知识，可以参考Information Processing and Learning。

码树

在介绍最优编码之前，首先介绍一下码树和Karft不等式。对于给定码字的全体集合，可以使用码树来表示。对于$r$进制的码树，如下所示，其中左图为二元码树，右边为三元码树。在码树中$R$点是树根，从树根伸出树枝，构成$r$元码树。

Karft不等式

对于$r$元字母表上的前缀编码，码字长度为$l_1,l_2,...,l_m$必须满足不等式

$$\sum_{i} r^{-l_{i}} \leq 1$$

反之，若给定满足以上不等式的一组码字长度，则存在一个相应的前缀码，其码字长度就是给定长度。其中$r$可以理解成一个节点最多的孩子节点的个数。

正向证明
假设$l_1 \leq l_2 \leq ... \leq l_{n}$，$A$表示$r$进制、深度为$l_{n}$的码树。对于使用$r$进制表示的$l \leq l_{n}$的任意字符，均能在码树$A$找到对应位置，进而第$i$个前缀编码在树$A$中对应节点是$v_{i}$。假设$A_{i}$表示以节点$v_{i}$为根的子树，此树的深度为$l_{n}-l_{i}$。根据树的性质可知，$A_{i}$叶节点的数量为

$$|A_{i}|=r^{l_{n}-l_{i}}$$

考虑到前缀编码的特性，子树之间不存在叶节点交叉，即：

$$A_{i} \cap A_{j} = \varnothing, i \neq j$$

因此

$$|\bigcup_{i=1}^{n} A_{i}|=|\sum_{i=1}^{n} A_{i}|=\sum_{i=1}^{n} r^{l_{n}-l_{i}} \leq r^{l_{n}}$$

其中$r^{l_{n}}$是所有也节点的数量。

反向证明
假设$l_1 \leq l_2 \leq ... \leq l_{n}$。从整个树的第$l_{1}$随机选择一个节点，使其对应第一个字符的编码。因为需要构建前缀编码，因此以该节点为根的子树所有节点都不再使用。这里假设整个这棵树的深度为$l_{n}$。因此不再考虑的节点个数为$r^{l_{n}-l_{1}}$。依次类推，不再考虑的节点个数为

$$\sum_{i=1}^{n}r^{l_{n}-l_{i}}$$

这时问题就转化为：不再考虑的节点个数是否比总的节点个数（$r^{l_{n}}$）多。由于满足Kraft不等式，因此可以构建前缀编码。

至此正向、反向证明均已完成。

最优编码

随机变量$X$的任一$r$元前缀码的期望长度

$$L \geq H_{r} (X)$$

当且仅当$r^{-l_{i}}=p_{i}$，等式成立。

$proof:$
上面的问题可以转化为

$$\min_{l_{i}} \sum_{i} p_{i}l_{i}\ \ subject\ to:\sum_{i}r^{-l_{i}}\leq 1$$

上面的问题可以转化为不等式约束下的拉格朗日数乘法，即

$$L(l_{i},\lambda,u)=\sum_{i}p_{i}l_{i}+\lambda(\sum_{i}r^{-l_{i}}-1-u^{2})$$

根据极值满足的条件得：

$$\begin{equation} \begin{cases} p_{i}-\lambda^{*}r^{-l_{i}^{*}}\ln{r}=0\\\\ \sum_{i}r^{-l_{i}}-1-u^{2}=0\\\\ -2\lambda u=0 \end{cases} \end{equation}$$

显然$\lambda\neq0$，则$u=0$。从公式一可知：

$$r^{-l_{i}}=\frac{p_{i}}{\lambda\ln{r}}$$

从公式二可知：

$$\sum_{i}r^{-l_{i}}=1=\sum_{i} \frac{p_{i}}{\lambda \ln{r}}=\frac{1}{\lambda \ln{r}}$$

故$\lambda^{*}=\frac{1}{lnr}$。进而$l^{*}_{i}=\log_{r}{\frac{1}{p_{i}}}$。此时最优编码的长度便是熵！

经过上面的证明可知，小明只需要用前缀编码，且码长满足$\log_{r}{\frac{1}{p_{i}}}$便可获得最优的编码长度。

总结

通过上面的讨论，我们找到了小明和小红信息交流的理论依据。在后面的博客中，我会带来更多知识！