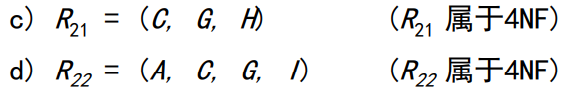---

前言

这是我根据以前做的笔记整理的范式与公理系统相关的知识点

---

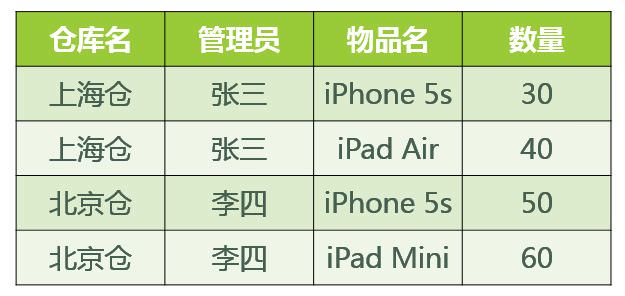
一、函数依赖

若在一张表中，在属性（或属性组）X的值确定的情况下，必定能确定属性Y的值，那么就可以说Y函数依赖于X，写作 X → Y

• 平凡函数依赖

$x\to y$ ;X函数确定Y，且Y包含于X中的属性

• 非平凡的函数依赖

$x\to y$ ;X函数确定Y，且Y不是X中的属性

• 决定因素

X可以确定Y则X是该函数依赖的决定因素

1.部分函数依赖

X,Y是关系R的两个属性集合，设存在X→Y，若X’是X的真子集，且存在X’→Y，则称Y部分函数依赖于X。

通俗的讲，部分函数依赖就是某一属性集的部分属性值即可确定另一属性集合的属性取值时，该两个属性集合之间存在部分函数依赖
只有当函数依赖的决定方是组合属性时，讨论部分函数依赖才有意义，当函数依赖的决定方是单属性时，只能是完全函数依赖。

2.完全函数依赖

设X,Y是关系R的两个属性集合，X’是X的真子集，存在X→Y，但对每一个X’都有X’!→Y，则称Y完全函数依赖于X。（Y依赖于X中的每一个属性）

也就是说，当从属性集合中去掉任一属性后，将不再存在函数依赖关系，这样的函数依赖称为完全函数依赖（依赖于属性组中的每一个属性）

3.传递函数依赖

在关系模式R(U)中，设X，Y，Z是U的不同的属性子集，如果X确定Y、Y确定Z，且有X不包含Y，Y不确定X，（X∪Y）∩Z=空集合，则称Z传递函数依赖于X。

4.码

由函数依赖我们可以对码进行如下定义

设 K 为某表中的一个属性或属性组，若除 K 之外的所有属性都完全函数依赖于 K，则称K为候选码

主属性：包含在某一候选码中的属性
非主属性：不包含在任一候选码中的属性

二、范式

1.第一范式（1nf）

关系中的每个属性都不可再分

2.第二范式（2nf）

每一个非主属性完全函数依赖于任何一个候选码

也就是说所有的非主属性必须由主键的全部属性来确定，不能存在这样一种情况：只凭借主属性组中的某一属性而确定了某一非主属性的值

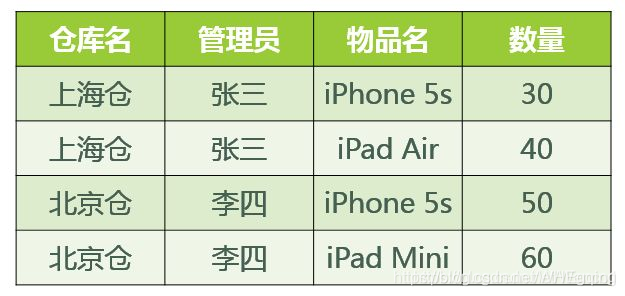
判断是否是第二范式

找出数据表中所有的码。
根据第一步所得到的码，找出所有的主属性。
数据表中，除去所有的主属性，剩下的就都是非主属性了。
查看是否存在非主属性对码的部分函数依赖。

3.第三范式（3nf）

表中的所有数据元素不但要能惟一地被主关键字所标识,而且它们之间还必须相互独立,不存在其他的函数关系

3nf在2nf的基础上，消除了非主属性对码的传递、部分函数依赖

4.BCNF范式

可以认为BCNF是扩充的3nf（3nf要求每一个非主属性即不传递也不部分依赖于任一个码，而bcnf在此基础上要求主属性也不能传递或部分依赖于码）每一个决定因素都包含码（也可以这样认为，bcnf中不允许有除了码之外的其它元素之间存在任何函数关系）

所有非主属性对每一个候选键都是完全函数依赖；
所有的主属性对每一个不包含它的候选键，也是完全函数依赖；
没有任何属性完全函数依赖于非候选键的任何一组属性

6.第四范式

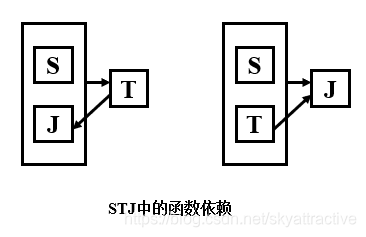
多值依赖

通过关系集合中的另一属性构建起两属性之间的依赖关系（间接关系）

第四范式是限制关系模式的属性之间不允许有非平凡且非函数依赖的多值依赖

---

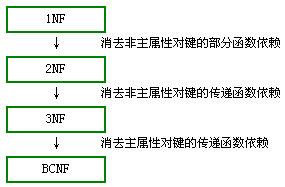
总结

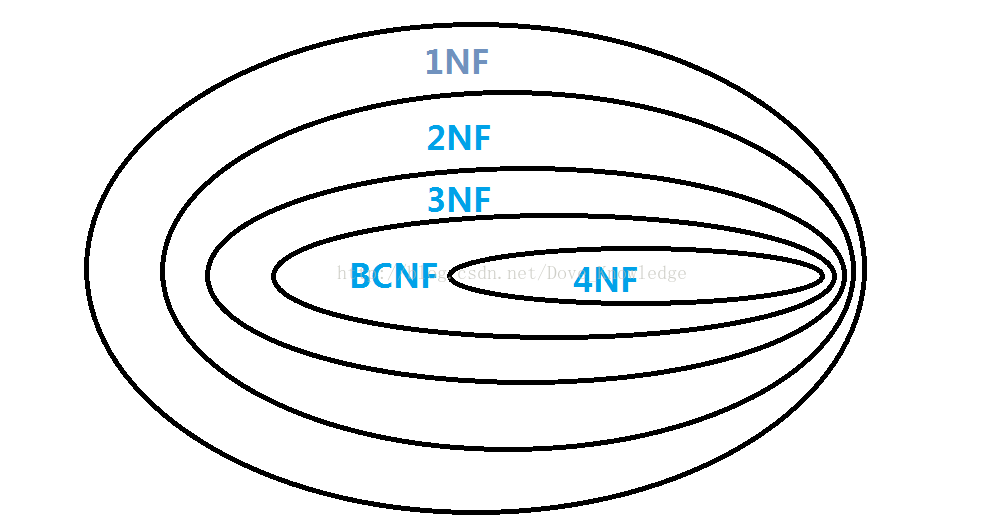
范式	解析
1nf	每一分量的值均为原子值
2nf	每一个非主属性完全函数依赖于任何一个候选码
3nf	每一个非主属性既不传递依赖于候选码，也不部分依赖于候选码
bcnf	非主属性对每一个码都是完全函数依赖；主属性对每一个不包含它的码都是完全函数依赖；没有任何属性完全函数依赖于非码的任何属性
4nf	各属性之间不允许拥有非平凡且非函数的多值依赖