回归分析（三）二项逻辑斯蒂回归

  学了一段时间突然又遇到逻辑斯蒂回归，结果发现已经忘完了，所以今天重新梳理一下。

（1）逻辑斯蒂分布

  先看一下逻辑斯蒂分布函数$F(x)$，其概率密度函数$f(x)$公式如下：
$$\begin{gathered} F(x)=P(X\le x)=\frac{1}{1+e^{\frac{-(x-\mu )}{\gamma }}} \\ f(x)=F^{\prime }(x)=\frac{e^{\frac{-(x-\mu )}{\gamma }}}{\gamma (1+e^{\frac{-(x-\mu )}{\gamma }}{)}^2} \\ （其中\mu 为位置参数，\gamma 为形状参数） \end{gathered}$$
  当$\mu =0,\gamma =1$时，即$sigmoid$函数如下：

$$sigmoid函数：F(x)=\frac{1}{1+e^{-x}}$$

（2）逻辑斯蒂回归数学推导

  逻辑斯蒂回归是在回归模型中引入$sigmoid$函数的一种非线性回归模型，如下：
$$\begin{array}{rl}& y=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-(w.x+b)}}\\ & 其中y\in (0,1),z=w.x+b\end{array}$$

• $sigmoid$函数的以下几条优秀性质，将赋予它以概率意义：

  • 单增有界，且取值范围为$(0,1)$，$F(0)=0.5$。

  • 对于输入$z$范围无限制，且$z\to \infty ,y=1;z\to -\infty ,y=0$。

 因此，逻辑斯蒂回归虽可用于数据和输出之间复杂关系回归拟合，但由于其良好的概率特性，使其更多情况作为二分类模型的基础。

​

  作二分类的逻辑斯蒂回归模型，即二项逻辑斯蒂回归，通过极大化似然函数的方法，运用梯度下降最优化模型参数，使得正确分类概率最大化，从而实现分类作用。

  这里我们引出逻辑斯蒂回归模型，它由条件概率分布表示，即输入$x$条件下，输出的概率分布：
P ( Y = 1 ∣ x ) = e ( w x + b ) 1 + e ( w x + b ) P ( Y = 0 ∣ x ) = 1 1 + e ( w x + b ) （ x ∈ R n 为输入， Y ∈ { 0 , 1 } 为输出， w ∈ R n 和 b ∈ R 为待优化参数， w 权值， b 偏置） P(Y=1|x)=\frac{e^{(wx+b)}}{1+{e^{(wx+b)}}}\\ P(Y=0|x)=\frac{1}{1+e^{(wx+b)}}\\ （x\in R^n为输入，Y\in \{0,1\}为输出，w\in R^n和b\in R为待优化参数，w权值，b偏置） P(Y=1∣x)=1+e(wx+b)e(wx+b)​P(Y=0∣x)=1+e(wx+b)1​（x∈Rn为输入，Y∈{0,1}为输出，w∈Rn和b∈R为待优化参数，w权值，b偏置）
  即对于给定的输入实例$x$，求解$P(Y=1|x)$和$P(Y=0|x)$，进行比较，将实例$x$分类到概率较大的一类即可。
$$\begin{array}{rl}插播tips:& \\ & 逻辑斯蒂回归也被称作--对数几率回归\\ & 几率odds=\frac{p}{1-p}/对数几率\log (odds)=log\frac{p}{1-p}\\ & 故对于逻辑斯蒂回归:\\ & \log \frac{P(Y=1|x)}{1-P(Y=1|x)}=\log \frac{P(Y=1|x)}{P(Y=0|x)}=w.x+b\\ & 故可理解，我们实际上是用线性回归模型去拟合逼近真实结果的对数几率。\end{array}$$
  接下来就是最大(对数)似然估计求解最优化参数即可：

  我们设$P(Y=1|x)=\pi (x),P(Y=0|x)=1-\pi (x)$。
$$\begin{array}{rl}& 似然函数：\prod _{i=1}^N[\pi (x_i){]}^{y_i}[1-\pi (x_i){]}^{1-y_i}\\ & 对数似然函数：L(w)=\sum _{i=1}^N[y_i\log \pi (x_i)+(1-y_i)\log (1-\pi (x_i))]\end{array}$$
  $L(w)$这玩意是不是看着很眼熟，那你看看下面这个式子：
$$二分类交叉熵损失函数：Loss(w)=-[y\log \hat{y}+(1-y)\log (1-\hat{y})]$$
  故最大化对数似然函数，其实和最小化损失函数是一个思路，故可用梯度下降法或牛顿法进行最优化参数求解。最小化损失函数是负迭代方向迭代，最大化似然函数正梯度方向迭代即可。

  接着对对数似然函数进行化简：
$$\begin{array}{rl}L(w)& =\sum _{i=1}^N[y_i\log \pi (x_i)+(1-y_i)\log (1-\pi (x_i))]\\ & =\sum _{i=1}^N[y_i\log \frac{\pi (x_i)}{1-\pi (x_i)}+\log (1-\pi (x_i))]\\ & =\sum _{i=1}^N[y_i(w.x)-\log (1+e^{(w.x)})]\\ （这里提& 一下，w.x就是之前的w.x+b,只是就行了扩展如下）\\ （w=(& w^{(1)},w^{(2)},...,w^{(n)})⟶(w^{(1)},w^{(2)},...,w^{(n)},b)）\\ （x=(& x^{(1)},x^{(2)},...,x^{(n)})⟶(x^{(1)},x^{(2)},...,x^{(n)},1)）\end{array}$$
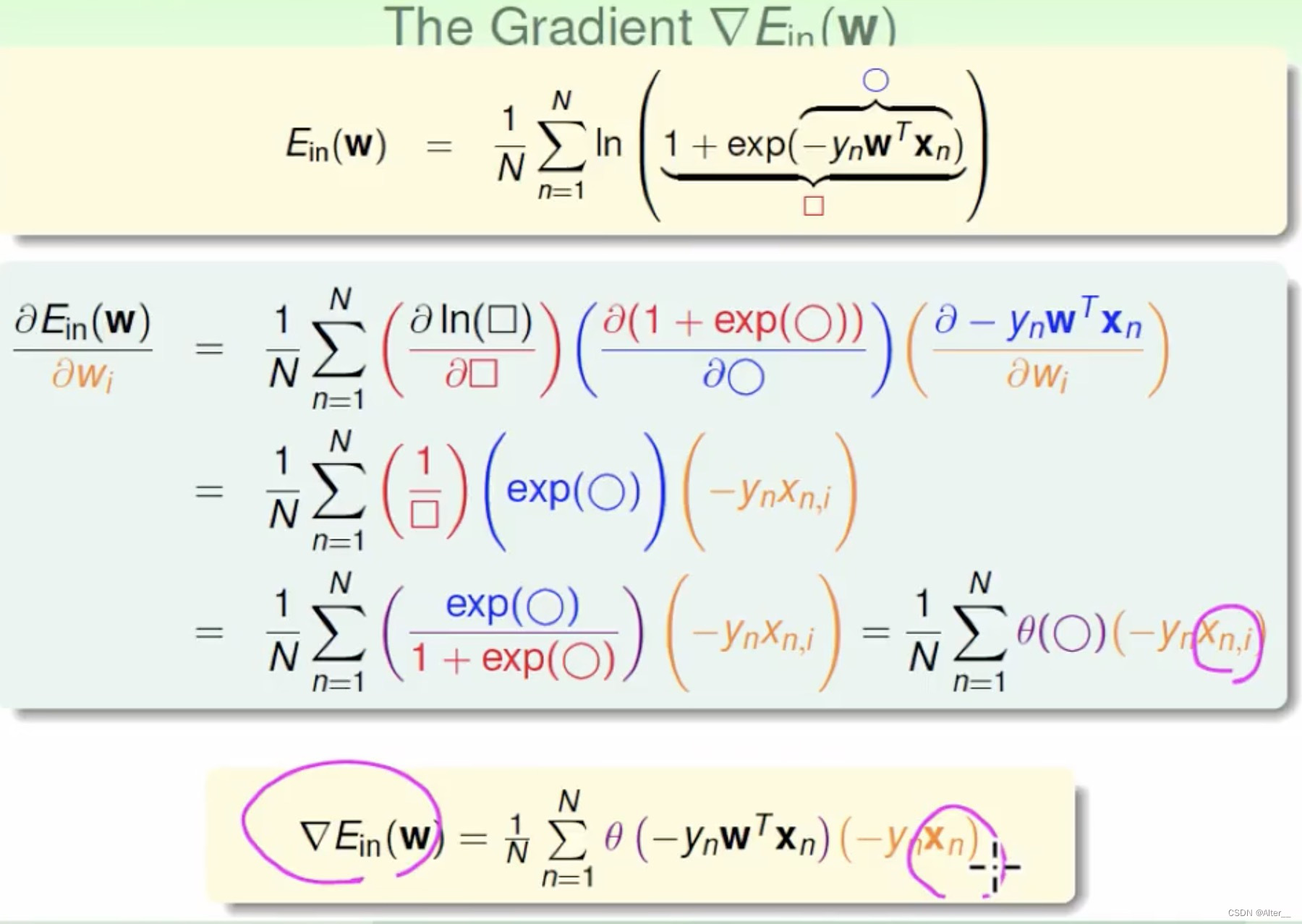
  我懒得写了，看看下面这个吧（这个博主那抄的：https://blog.csdn.net/daaikuaichuan/article/details/80848958）

  感觉上式$\ln$只是说明是对数似然函数，不需要取对数$\ln$。得到个分量偏导，就是对每个参数分量进行一个学习步长$\alpha$的偏导方向的优化，直到对数似然函数$L(w)$不再显著提升，或达到最大迭代次数。