目录
一、分类与回归
二、逻辑回归不是回归
三、生成式逻辑回归
四、判别式逻辑回归
五、逻辑回归为什么不用均方误差做损失函数
六、判别模型与生成模型的比较
七、写在最后
一、分类与回归
回归与分类是机器学习的基本问题。回归是预测连续值,分类是预测离散值;回归的输出可以是任意值,而分类的输出只能是预设的分类输出的一个,比如(0,1)中的0或1.;理论上讲,如果回归的输入值相近,那么它的预测值也是相近的,而分类的输入相近(在同一个分类决策边界内),那么它们的预测值是一样的,代表属于同一类别。
举个例子:
预测明天的气温是回归问题,因为预测值可以是正常温度中的任意一个值,是连续的。
预测明天的天气是分类问题,它的预测值是阴、晴、雨等等,是离散的。
二、逻辑回归不是回归
逻辑回归,Logistic Regression,名为回归,实为分类算法。
逻辑回归的激活函数为:
通过计算,它的输出为(0,1)之间的某个数值,代表概率,输出值越接近1,表示判断为正的概率越大。和回归的区别在于,输出不能为连续的任意值,只能介于零一之间,而通过设置阈值θ,如果f(x)>θ,则最终输出为1,代表分类为正样本。如果输出f(x)<θ,输出为0,代表分类为负样本。所以逻辑回归不是回归而是分类。
三、生成式逻辑回归
假设我们有一个数据集,共有1000个样本,其中C1类有350个,C2类有650个。那么我们就已知了P(C1)和P(C2)。
贝叶斯公式为:
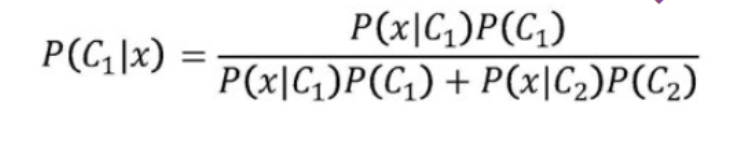
由贝叶斯公式上下同时除以分子可得:
令 则
(sigmoid函数)
sigmoid函数的性质如下图:
它可以完美的实现逻辑回归输出的要求,输出结果在(0,1)。所以逻辑回归以此为激活函数。
考虑到公式Z:
而对于一个样本,比如我们之前提到的,P(C1)H和P(C2)是已知的,只需要求前面一项即可。
现在假设每个特征的维度相互独立,则:
假设样本C1C2的分类均为高斯分布,且相互独立,则C1样本的均值为,样本方差为Σ1;C2的样本均值为
,样本方差为Σ2。则:
通过计算最终可得:

其中最后一项为先验概率比值的ln值。
当我们不采用单独的方差,而是使用协方差矩阵代替,即Σ=Σ1=Σ2,那么问题将得到简化,
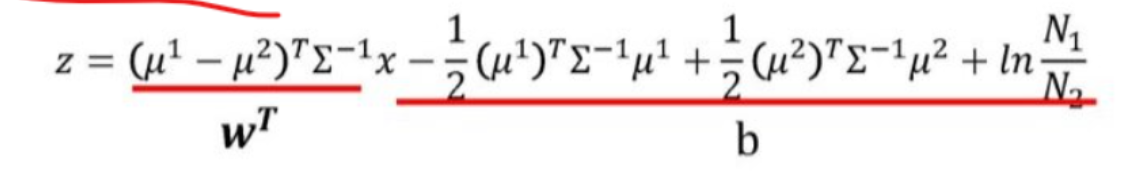
即:
这样通过先验概率和假设特征概率分布而求得参数的方法,成为生成式逻辑回归模型。
四、判别式逻辑回归
我们在线性回归时直接规定了损失函数为MSE,通过优化损失函数来求得最终的参数,那么我们可不可以直接也用MSE作为逻辑回归的损失函数而直接求参数呢?答案是否定的。当然,并不是因为不能优化损失函数来求参数,而是MSE不适合作为线性回归的损失函数。既然MSE的求距离方式不适用,那么我们可不可以找到另外一种求距离的方式来优化呢?答案是肯定的。那就是KL散度。

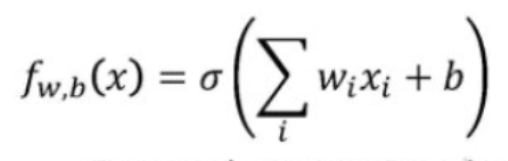
通过这一步,可以使输出值变为(0,1)内的一个概率值。
令(其中x1与x2为一类,x3为另一类):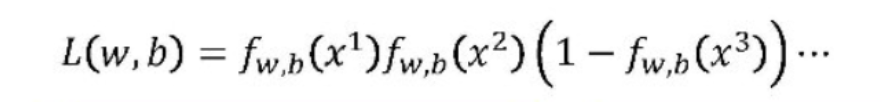
我们要找出一对(w,b),使L(w,b)最大,这样就可以使x1x2为一类且x3为另一类的概率最大,即在训练集上的误差最小。
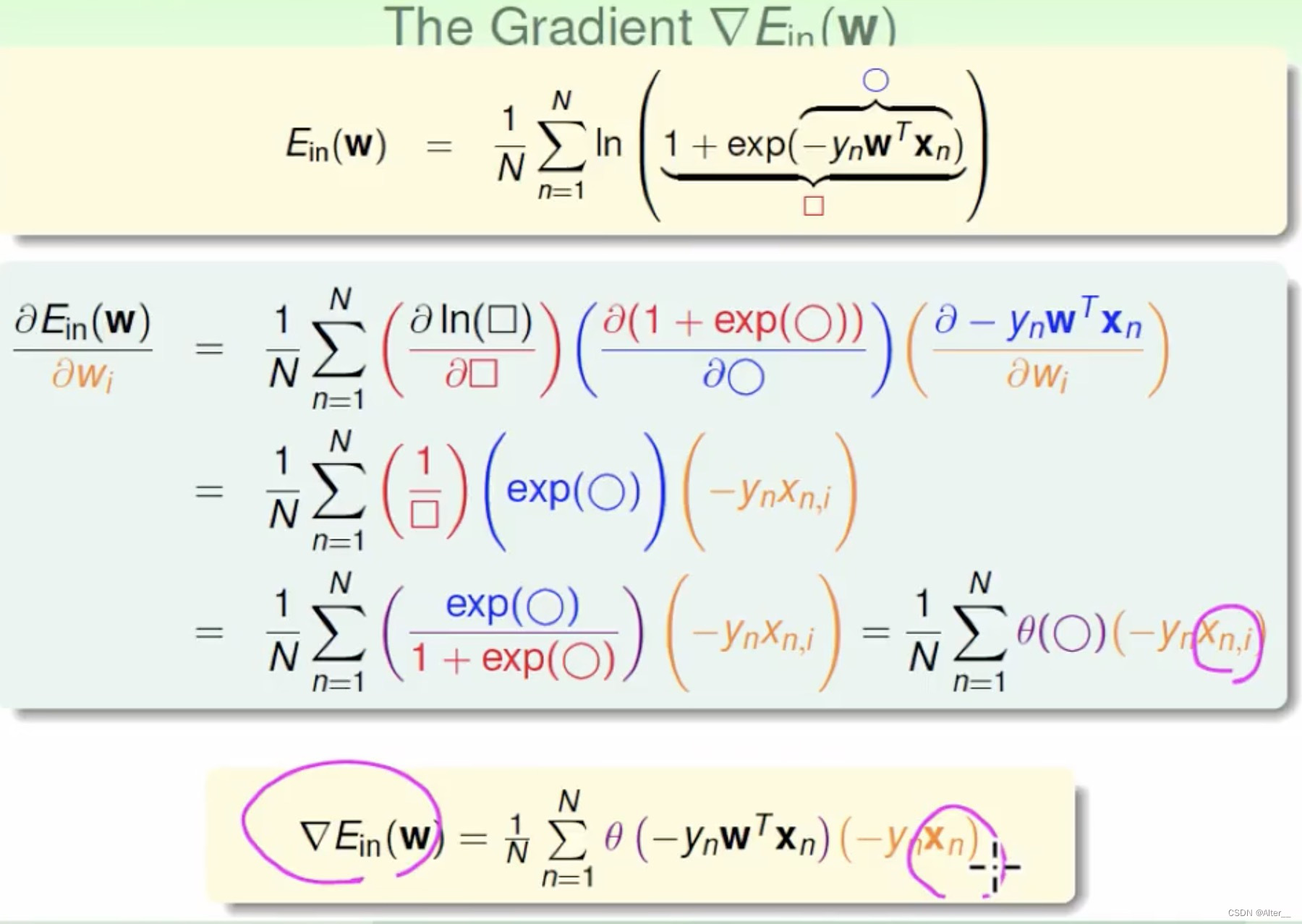
最大化L(w,b)就是最小化 {-ln(L(w,b))}
这就是两个伯努利分布的交叉熵损失函数。
接下来就可以对w和b采用梯度下降或者其他优化算法求最优值了。方法和线性回归类似,这里不再详细推导。
五、逻辑回归为什么不用均方误差做损失函数
假如损失函数为均方误差,则:
由sigmoid函数特性可知,当初始化一组(w,b)后,f(x)的值接近0或者1的概率非常大,那么梯度值就会接近零,而根据更新公式:
当梯度值接近0时,每次更新幅度几乎为零,就会被判定更新到最优质。而实际上并没有进行任何优化,这显然是无法接受的。
既然我们选的初始(w,b)导致梯度为0,那么我们可以多次初始化,从中选择一个好的( w,b)进行优化吗?理论上可以,但现实非常难。
另外,MSE的局部最优值与特征数量的平方称正比,所以会非常容易陷入局部最优。而KL散度最为优化函数,因为是凸函数,所以是一定可以求得全局最优的。
六、判别模型与生成模型的比较
ng和Jordan的神论文《On Discriminative vs. Generative classifiers: A comparison of logistic regression and naive Bayes》的论文中提到:
判别式分类器才是首选。当训练集增加,尽管两种算法都会表现更好,但效果好的表现形式却是不同的。从反复实验中观察到,训练集增加后,判别式方法会达到更低的渐进误差,而生成式方法会更快的达到渐进误差,但这个误差比判别方法的渐进误差大。
而从我们上述推到过程中也可以发现,生成模型我们进行了诸多假设,这些假设可以使噪声的影响被抵消,所以生成式模型受样本数据的影响较小,而判别式模型受数据和噪声影响更大。
七、写在最后
我是一个刚接触机器学习不久的小白,借着写博客来记录一下学习历程并加深理解,文中难免有错误,若您读后发现有错误,望不吝赐教,谢谢。