逻辑斯蒂回归分类算法
首先来看一个线性回归来进行分类的问题: 怎样判断肿瘤是否恶性?

很明显线性回归用于分类问题无法处理边界点的位置。
同时,线性回归健壮性不够,一旦有噪声,立刻“投降”

使用逻辑斯蒂回归 —— 分类问题

Sigmoid函数(压缩函数)
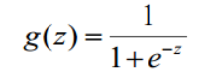

sigmoid函数中,e-z 中 z 的正负决定了 g(z) 的值最后是大于 0.5 还是小于 0.5;即 z 大于 0 时,g(z) 大于 0.5,z 小于 0 时,g(z)小于 0.5
当 z 对应的表达式为分类边界时,恰好有分类边界两侧对应 z 正负不同,也就使得分类边界两边分别对应 g(z)>0.5 和 g(z)<0.5,因此根据 g(z) 与 0.5 的大小关系,就可以实现分类
来看两个示例:

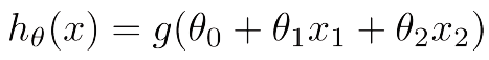
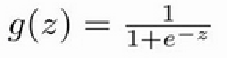
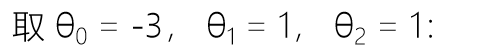
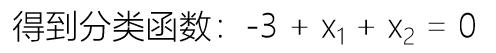
我们将线性回归拟合出来的值用压缩函数进行压缩,压缩完成后用 0.5 做一个概率的判定边界,就能把样本分成两类,即正样本和负样本

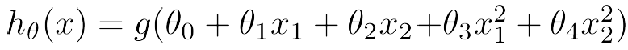
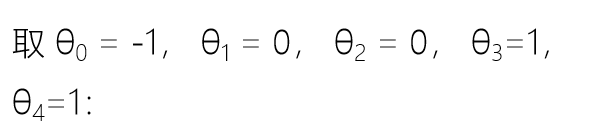
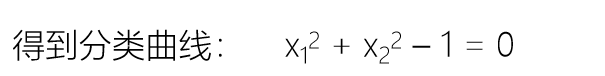
逻辑斯谛回归损失函数
- 平方损失函数的问题

如果使用梯度下降法求解算法可能无法得到全局最优解,最小二乘法求解不适用于多元函数。
我们期待的损失函数为一个凸函数,可以使用梯度下降求解最优质值。

考虑到对数函数中可以根据零点将数据定义划分为正类和负类:

因此,在逻辑回归分类算法中,我们的损失函数定义如下:
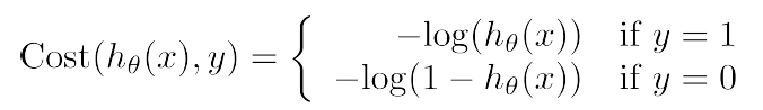


因此,在逻辑回归分类算法中,我们的损失函数定义如下:


梯度下降法求解
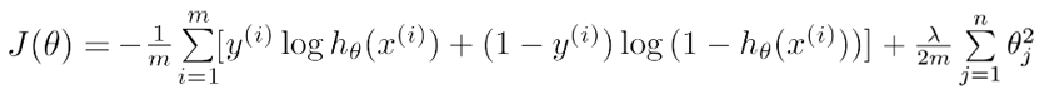
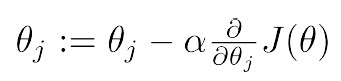
代码案例
import numpy as np
import pandas as pdfrom sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.datasets import load_irisimport matplotlib as mpl
import matplotlib.pyplot as pltif __name__ == "__main__":#引入sklearn里面的数据集,iris鸢尾花iris = load_iris()df = pd.DataFrame(data = iris.data, columns = iris.feature_names)df['class'] = iris.targetdf['class'] = df['class'].map({0:iris.target_names[0], 1:iris.target_names[1], 2:iris.target_names[2]})#path = 'iris.data'#data = pd.read_csv(path, header=None)#对类别进行编码df[4] = pd.Categorical(data[4]).codes#划分训练集测试集x,y = np.split(data.values, (4,), axis=1)x = x[:, :2]#创建训练模型lr = Pipeline( [('sc',StandardScaler()),('poly',PolynomialFeatures(degree=2)),('clf',LogisticRegression())] )lr.fit(x, y.ravel())y_hat = lr.predict(x)y_hat_prob = lr.predict_proba(x)np.set_printoptions(suppress=True)#print('y_hat = \n', y_hat)#print('y_hat_prob = \n', y_hat_prob)print('准确率:%.2f%%' % (100 * np.mean(y_hat == y.ravel())))# 画图N, M = 500, 500 # 横纵各采样多少个值x1_min, x1_max = x[:, 0].min(), x[:, 0].max() # 第0列的范围x2_min, x2_max = x[:, 1].min(), x[:, 1].max() # 第1列的范围t1 = np.linspace(x1_min, x1_max, N)t2 = np.linspace(x2_min, x2_max, M)x1, x2 = np.meshgrid(t1, t2) # 生成网格采样点x_test = np.stack((x1.flat, x2.flat), axis=1) # 测试点mpl.rcParams['font.sans-serif'] = ['simHei']mpl.rcParams['axes.unicode_minus'] = Falsey_hat = lr.predict(x_test) # 预测值y_hat = y_hat.reshape(x1.shape) # 使之与输入的形状相同plt.figure(facecolor='w')plt.pcolormesh(x1, x2, y_hat) # 预测值的显示plt.scatter(x[:, 0], x[:, 1], c=np.squeeze(y), s=50) # 样本的显示plt.xlabel('花萼长度', fontsize=14)plt.ylabel('花萼宽度', fontsize=14)plt.xlim(x1_min, x1_max)plt.ylim(x2_min, x2_max)plt.grid()plt.title("Logistic回归-鸢尾花", fontsize=17)plt.show()