前言

预测任务分为：

1. 回归问题：输入、输出变量为连续变量。
2. 分类问题：输出变量为有限个离散变量。
3. 标注问题：输入、输出变量为变量序列。

前面提到用感知机进行分类时，得到了是离散变量。但是实际上是因为$sign$函数，如果用这个函数，不就是线性回归了嘛！
逻辑斯蒂回归(logistic distribution)模型适用于多类分类问题，它是对数线性模型，属于判别模型。它源自于逻辑斯蒂分布。
优点：计算代价不高，易于理解和实现。
缺点：容易欠拟合，分类精度可能不高。

逻辑斯蒂分布

首先我们需要知道什么是$sigmoid$函数？
$sigmoid$是一个在生物学中常见的S型生长曲线，$sigmoid$函数常被用作神经网络的激活函数。
$$\theta (x)=\frac{1}{1+e^{-x}}$$

这个曲线以点$(u,\frac{1}{2})$为中心对称，而且在中心附近增长速度较快，在两端增长速度较慢。取值范围为$(0,1)$，它可以将一个实数映射到$(0,1)$的区间，可以用来做二分类。逻辑斯蒂函数，也就是逻辑斯蒂分布的分布函数与它一样。密度函数是一个凸函数。

个人认为sigmoid函数和logisitic函数差别不大
参考：https://baike.baidu.com/item/Sigmoid%E5%87%BD%E6%95%B0/7981407
https://baike.baidu.com/item/%E9%80%BB%E8%BE%91%E6%96%AF%E8%B0%9B%E5%88%86%E5%B8%83/19127203#reference-[1]-19510388-wrap

模型

之前的是在$w^{T}x+b$外面加上$sign$函数，现在直接将$sign$函数替换为$sigmoid$函数，上图为$\theta (\cdot )$。两者的区别在于损失函数的计算。

二项逻辑斯蒂回归模型

顾名思义，解决二分类问题。


把$b$放入$w$，$x$多一个$1$还是很好理解的，矩阵展开就行了。公式6.5分子分母除以分子，就变得和$sigmoid$函数一致。公式6.6直接是因为sigmoid的对称性，由公式6.6推来。

多项逻辑斯蒂回归模型

用于多分类问题：

策略

在逻辑斯蒂回归模型中，单看等式左边$P(Y=y|x)$很明显是一个条件概率。等式右边直接用$\theta (\cdot )$代替，明显是个关于$w$的公式，因为实际问题中$x$是已知的。
如果$\theta$是已知确定的，$x$是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点$x$，其出现概率是多少。
如果$x$是已知确定的，$\theta$是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现$x$这个样本点的概率是多少。似然问题：关于模型的参数$\theta$是未知的。所以逻辑斯蒂回归求解模型参数是一个似然问题。

用极大似然估计法估计模型参数。极大似然估计法，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！

我们希望得到一个好的模型，策略就是每一个样本分类正确的概率能够尽可能大（你也不想你的分类可信度低或者错误分类概率变大吧，所以样本和正确分类事件要同时满足哦），每个样本还是独立同分布的。那么策略就是
$$max\prod P(x,Y=y)=max\prod P(Y=y|x)P(x)$$其中$Y=y是x的正确分类，P(x)是常数，P(Y=y|x)=\theta (\cdot )$。常数我管不着，化简我能做的就是，剩下的就是优化目标了，这里我们把判断是不是样本正确分类也交给了指示函数来做判断。
$$max\prod P(Y=y|x)\to max\prod _{i=1}^N\prod _{k=1}^{K}p(Y=k|x_i{)}^{\mathbb{I}(k==y_i)}$$其中$k$表示某个分类，$y_i$代表样本$x_i$的真实分类，$\mathbb{I}$是指示函数。到目前为止极大似然函数已经得出。乘法不好求，取一个对数吧。
$$max\prod _{i=1}^N\prod _{k=1}^{K}p(Y=k|x_i{)}^{\mathbb{I}(k==y_i)}\to max\sum _{i=1}^N\sum _{k=1}^K\mathbb{I}(k==y_i)ln(p(Y=k|x_i))$$
$max$转换为$min$方便参数优化。
$$max\sum _{i=1}^N\sum _{k=1}^K\mathbb{I}(k==y_i)ln(p(Y=k|x_i))\to min\sum _{i=1}^N\sum _{k=1}^K-\mathbb{I}(k==y_i)ln(p(Y=k|x_i))$$
进一步把$p$变为$\theta$函数，求解参数。在此之前，需要确认指示函数，二项逻辑斯蒂回归：
$$\mathbb{I}=\{\begin{array}{cc}{y}_i,& y_i=1\\ 1-y_i,& y_i=0\end{array}$$
其中，$$p(Y=1|x)=\theta (w^T\cdot x)=\frac{1}{1+e^{-w^T\cdot x}}$$
对数似然函数变为：
$$min-\sum _{i=1}^N{y}_{i}ln(\theta (w^T\cdot x_i))+(1-y_i)ln(1-\theta (w^T\cdot x_i)))$$把$(1-y_i)$拆开，并把$sigmoid$带入,最终得到
$$min-\sum _{i=1}^N[y_i(w^T\cdot x_i)-ln(1+e^{w^T\cdot x_i})]$$再次说明，$y_i$是标量，$w,x_i$是列向量哦。

算法

1. 写出似然函数
2. 写出对数似然函数
3. 求对数似然函数的最大值，得到参数w的估计值。

如何求对数似然函数的最大值

1. 凸函数的局部最优解就是全局最优解。
2. 逻辑斯蒂回归函数就是凸函数(结论直接用，想要证明看链接)。

梯度下降法

在上面这两个条件下使用梯度下降法求逻辑斯蒂回归的参数。梯度下降法是求解无约束最优化问题的一种最常用的方法，实现简单。简单的来说就是一步一步迭代求解目标函数的梯度向量。

算法思想

1. 初始化：步长λ，参数w，精度ε。（步长是多个；参数可以经验取也可随机；精度是误差，要取小一些）
2. 根据目标函数f，对参数w求梯度$w^{{}^{\prime }}$。
3. 然后开始循环迭代，$w_{t+1}=w_t-\lambda \ast w_t^{{}^{\prime }}$。
4. 什么时候迭代结束呢？我们可以做出如下选择，一般选择2和3一起：
   （1. 可以设置迭代一定次数就结束；
   （2. 每一次迭代我们在最后计算如果：$f(w_{t+1})-f(w_t)＜\epsilon$就结束；
   （3. 每一次迭代我们在最后计算如果：$w_{t+1}-w_t＜\epsilon$就结束；
   （4. 用测试集计算精准度，够了就结束

推导公式

参考：https://www.bilibili.com/video/BV1t54y1Q76V?from=search&seid=1402616765635404394
https://www.bilibili.com/video/BV164411b7dx?p=10

注意

林轩田课程中，逻辑斯蒂回归有些不一样，是因为类别不是0和1，而是-1和1。如果用-1和1，那么上面说的指示函数$\mathbb{I}$会出问题。

$Probability\approx Likelihood$，那么$f(x)\approx h(x)=\theta (w^{T}x)$。还利用了$sigmoid$的对称性，将$y_i$挪到$\theta$函数中，


老操作了，加log，加负号。

这个函数的求导：

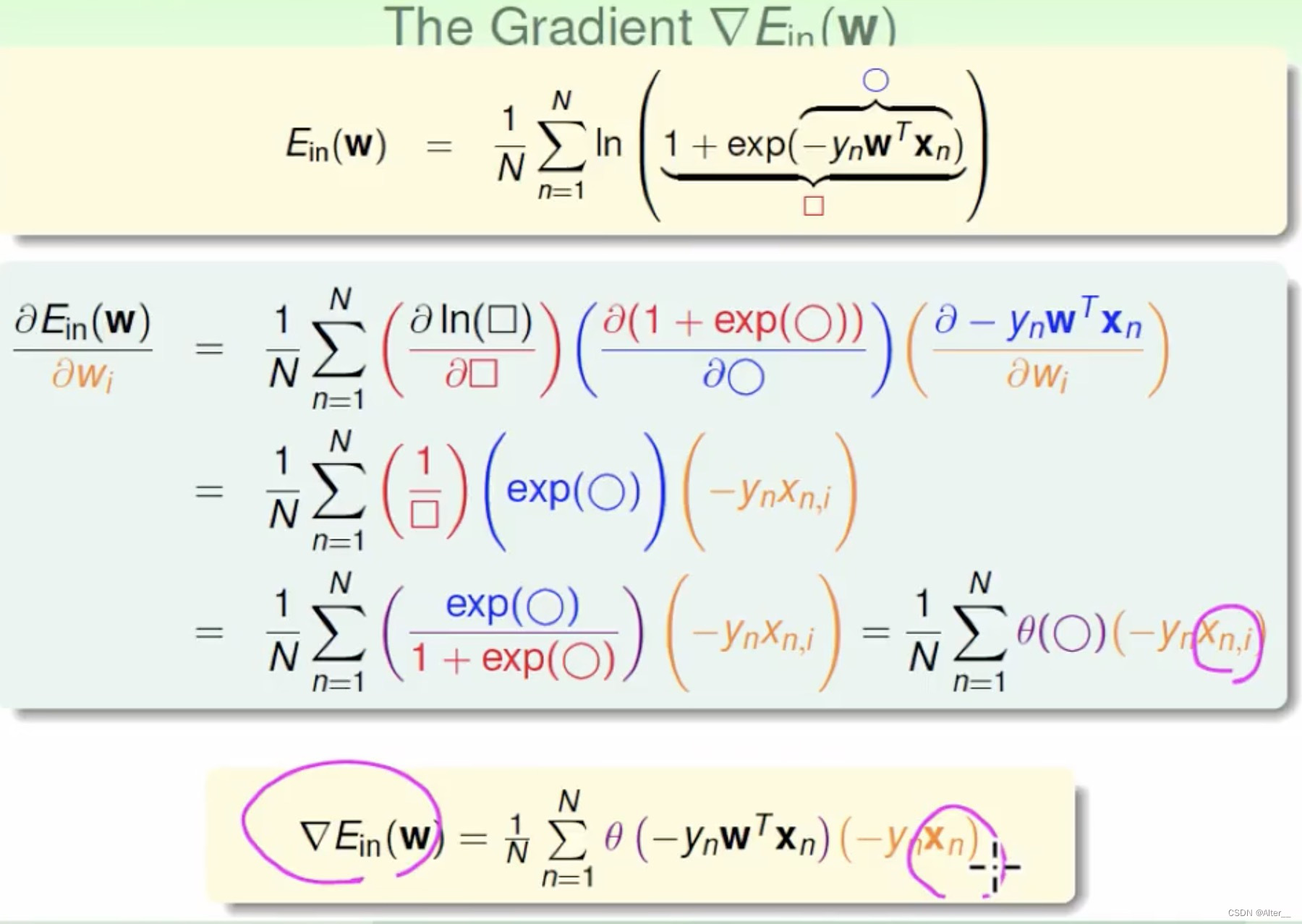
所以，最终你可以发现，两种类别设置的最终导数形式不一样。

全文参考

逻辑斯蒂回归加上正则化罚项，L1范数，绝对值求导：https://zhuanlan.zhihu.com/p/463149304
二项逻辑斯蒂回归的梯度计算：https://zhuanlan.zhihu.com/p/44591359
林轩田相关课程：https://www.bilibili.com/video/BV1Cx411i7op?p=39&vd_source=3e4efd7b4c6de427a4d3667989b3bd71
损失推导(多项的逻辑斯蒂回归形式与统计学习方法上写的不一致)：https://zhuanlan.zhihu.com/p/65594209