1、概述
Barabási和Albert(1999)的“富者更富”(Rich get richer)生成模型(BA模型)最被熟知的无标度网络子集的生成模型。它让每个网页根据一个非均匀的概率分布与已有网页建立连接,这个概率分布与当前网页的入度数成比例。根据这个过程,拥有更多入度的的网页相较一般网页会吸引更多的链接。这样的机制会产生“幂律”(Power Law)。
和无标度网络相关的另外一个耳熟能详的名词是“长尾效应”。
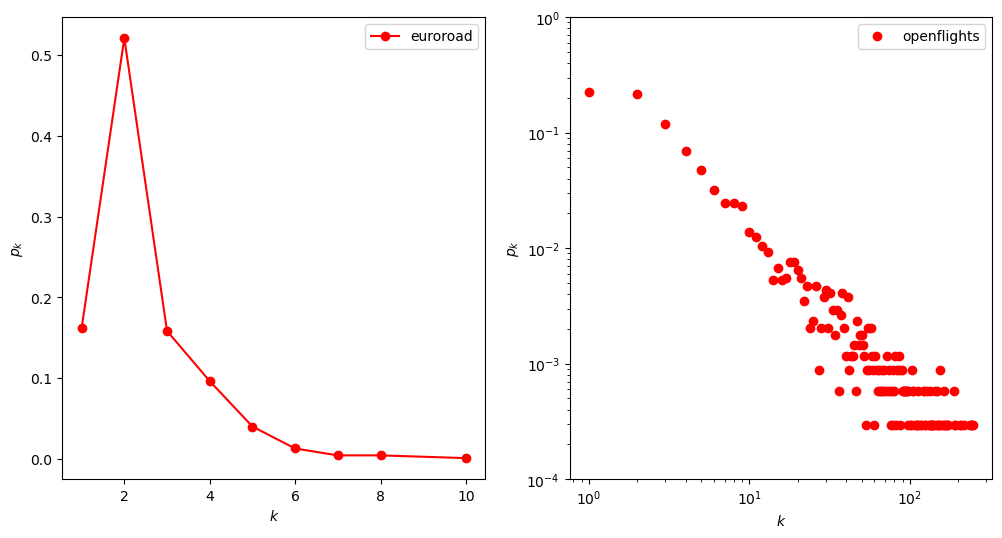
无标度网络(scale-free network)是一种度分布(即对复杂网络中节点度数的总体描述)服从或者接近幂律分布的复杂网络。尽管许多真实世界的网络被认为是无标度的,然而其证明却往往因为愈发严格的数据分析技术而显得不够充分。由此,许多网络的无标度性还在科学社群中被争讨论中。一些声称是无标度的网络包括:
• 社交网络(Social networks),包括合作网络。两个被广泛研究的示例是演员合演电影的合作网络和数学家合著论文的合作网络。
• 许多种电脑网络,包括互联网和万维网的网图。
• 一些金融网络,如银行间支付网络。
• 蛋白质-蛋白质相互作用网络。
• 语义网络[3]。
• 航空航线网络。
BA图/无标度图拥有以下特征:
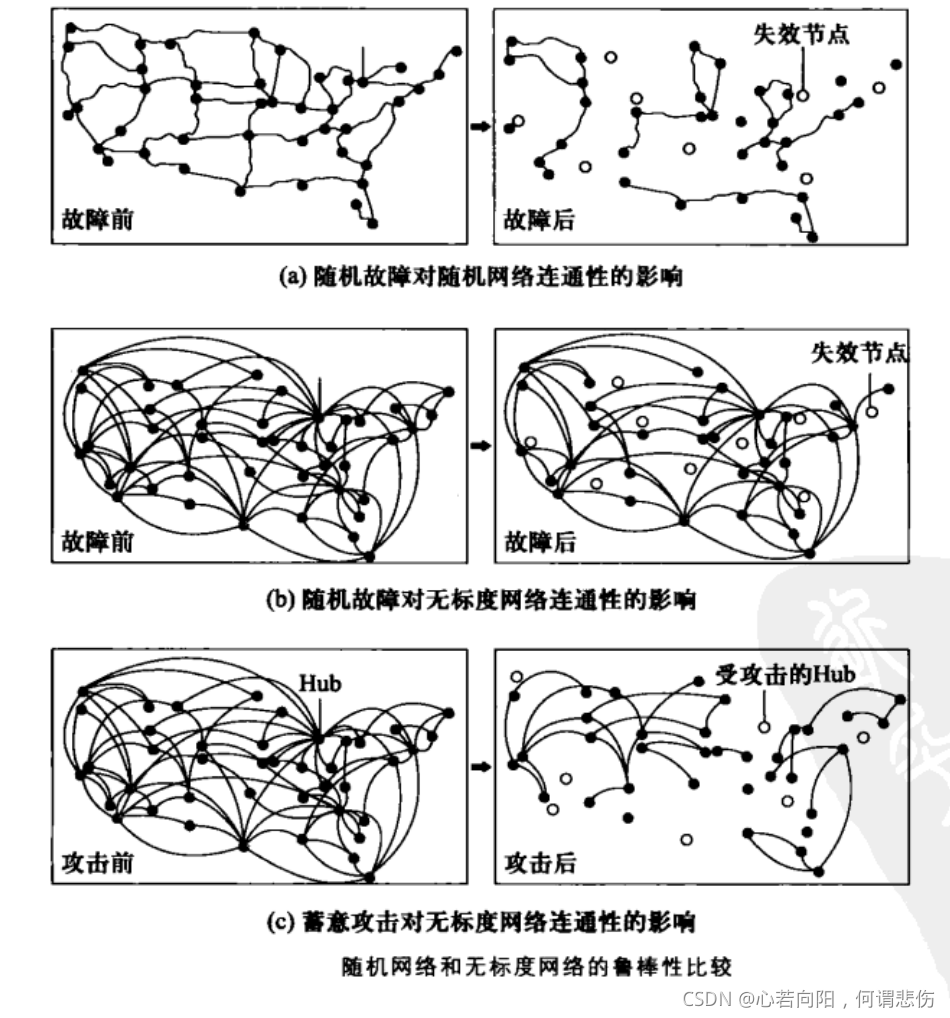
- 普遍存在度远高于平均值的节点。度最高的节点通常称为枢纽(hub),被认为在网络中起到特殊作用,尽管这还要看具体在网络的哪个区域。无标度性与网络应对故障的鲁棒性有很大关系。主要的hub节点通常连接着小的hub节点。这些小的hub节点再伴随着度更小的节点,
- 无标度图的层级关系使得网络拥有一定的容错行为。如果错误随机发生,并且大量节点都具有较小的度,那么hub节点受影响的概率微乎其微。即便hub节点出现了错误,因为还有其他hub节点,网络通常不会失去原来的连通性。然而,如果定向选择一些主要的hub节点并把它们从网络中去除,网络便会转为许多相对离散的图。因此,hub节点既是无标度网络的优势又是劣势。
- 随节点度数升高而降低的聚集系数(clustering coefficient)分布。这个分布也服从幂律分布。这表明度数低的节点从属于致密的子图,这些子图再通过hub节点互相连接。试想一个社交网络,它的节点是人,而链接是熟人关系。很容易得出人们倾向于形成社群,也就是互相熟识的团体。
- 在实践中,一个生长中的无标度网络的半径几乎可以被认作是一个定值。
2、过程调用接口
| 过程接口 | CALL apoc.generate.ba( noNodes, edgesPerNode, label, relType ) |
| 参数名 | 类型 | 缺省值 | 可为空? | 说明 |
| noNodes | 非负长整数 | 1000 | 是 | 随机生成的节点总数。 |
| edgesPerNode | 非负长整数 | 2 | 是 | 每个节点的边的数量的一半。实际生成图时会按照这个数值生成出边和入边,因此会有2倍的边。 |
| label | 字符串 | NULL | 是 | 节点标签。如果为空则缺省为Person,并且会为每个Person节点生成一个英文名字保存在name属性中。 |
| relType | 字符串 | NULL | 是 | 关系类型。如果为空则缺省为FRIENDS_OF。 |
3、示例
// 8.7(1) 生成一个有10万节点、80万条边的BA图。
// 节点标签为NodeBA,边/关系类型为LINKS4。
// 执行时间:1872msCALL apoc.generate.ba(100000,4,'NodeBA', 'LINKS4') // 8.7(2) 统计生成的图中、节点度的分布。MATCH (u:NodeBA)
WITH size ((u) -- ()) AS countOfRels
WITH countOfRels, count(countOfRels) AS cnt
RETURN countOfRels, cnt
ORDER BY countOfRels ASC
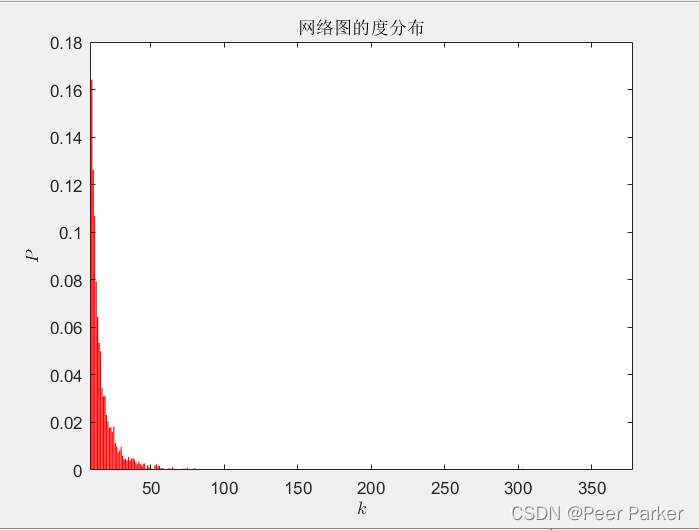
运行8.7(1)和8.7(2)中的查询后,我们可以得到下面的结果(图中仅显示到度数<200的节点):
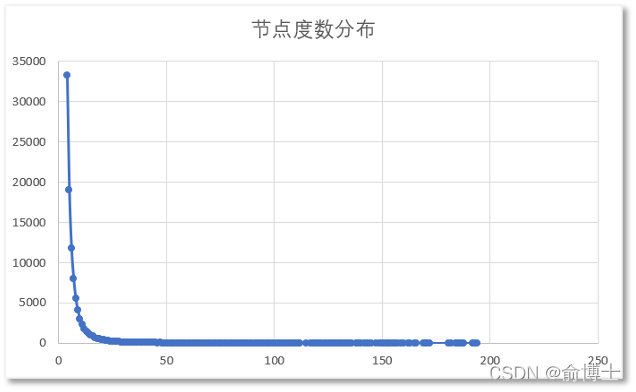
从上图中可以清晰地看到,无标度网络中只有少量节点有很高的度(即边的数量,从而符合幂律、而不是随机分布),而绝大多数节点的度非常少(长尾)。