网络节点的度没有明显的特征长度我们就称之为无标度网络。
一、BA无标度网络模型
1、模型概述
ER随机图和WS小世界模型忽略了实际网络的两个重要特性:
(1)增长特性:即网络的规模是不断扩大的。例如每个月都会有大量的新的科研文章发表,www上则每天都有大量新的网页产生。而ER随机图和WS小世界模型中网络节点数是固定的。
(2)公先连接特性:即新的节点更倾向于与那些具有较高连接度的hub节点相连接。这种现象也称为“富者更富”或“马太效应”。 例如,新发表的文章更倾向于引用一些已被广泛引用的重要文献,新的个人主页上的超文本链接更有可能指向有影响的站点。而在ER随机图中,两个节点之间是否有边相连是完全随机确定的,在WS小世界模型中,长程边的端点也是完全随机确定的。
基于上述增长和优先连接特性,前人们又提出了BA无标度网络模型,构造算法如下:
(1)增长:从一个具有m 0 _0 0个节点的连通网络开始,每次引入一个新的节点并且连到m个已存在的节点上,这里m<=m 0 _0 0。
(2)优先连接:一个新节点与一个已经存在的节点i相连接的概率与节点i的度k i _i i之间有如下关系:
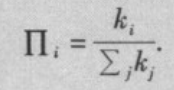
在经过t步后,BA算法产生一个包含N=t+m 0 _0 0个节点和mt +M 0 _0 0条边的网络,其中M 0 _0 0是初始时刻t=0的m 0 _0 0 个节点之间存在的边数。
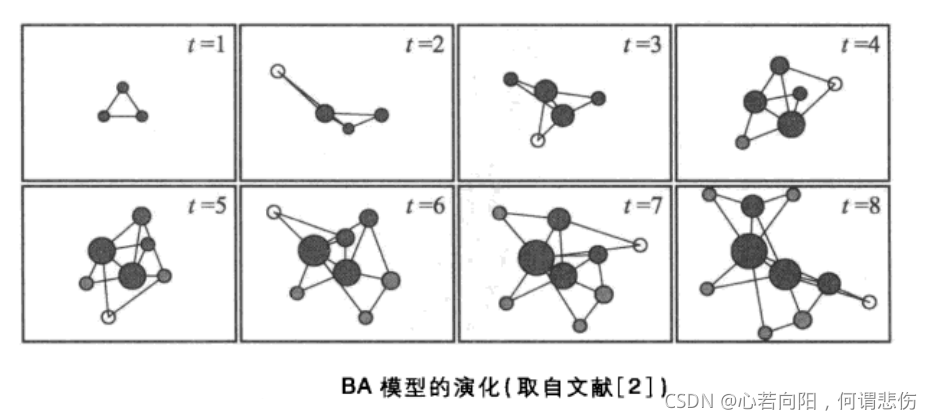
下图显示了参数为m 0 _0 0=M 0 _0 0=3、m=2的BA网络的演化过程。已有节点用实心圆点表示,实心圆点的相对大小对应于节点度的相对大小。每次新增加的一个节点用空心圆点表示,它按优先连接机制与网络中已有的两个节点相连。
2、幂律度分布
BA模型具有幂律度分布且与参数、网络规模N均无关。
对BA模型的度分布的理论分析可以有多种方法,包括主方程方法、率方程方法和更为简洁的近似方法即平均场理论。 在复杂网络分析中,这几种方法得到的渐近结果往往都是相同的。
2.1 平均场理论
假设初始网络有m 0 _0 0个节点,并记时刻t节点i的度为k i _i i(t)。对充分大的t,可忽略初始网络中的M 0 _0 0条边并有m 0 _0 0+t ≈ \approx ≈t。当一个新节点加入到系统中来时,节点i的度改变(即增加1)的概率为:
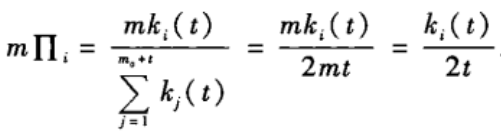
现在用平均场理论对BA模型的度分布做近似分析,为此需要给出如下的连续化假设:
(1)时间t不再是离散的,而是连续的;
(2)节点的度值也不再是整数,而是可以为任意实数。
在这两个假设下,上式概率公式可以解释为节点i的度的变化率,从而可以把网络演化近似转化为单个节点演化的平均场方程:
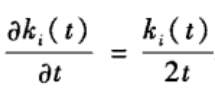
假设节点i是在时刻t i _i i加入网络的,那么上面微分方程的初始条件为k(t i _i i)=m。于是求得:
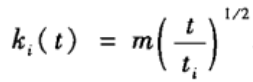
假设当时间t-> ∞ \infty ∞时,度分布P(k(t))收敛于稳态度分布P(k)。由概率定义有:
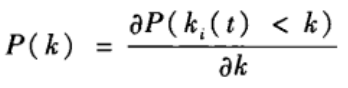
可得:
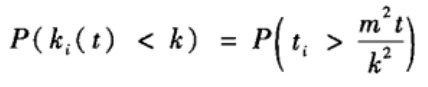
假设是以相等的时间间隔添加节点的,那么t i _i i的概率密度为:
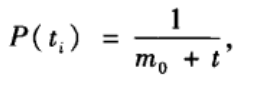
从而有:
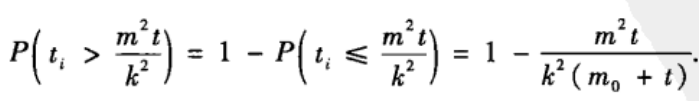
可得:
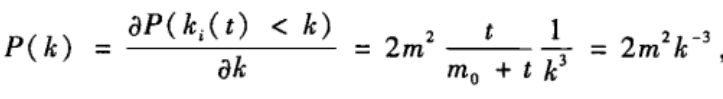
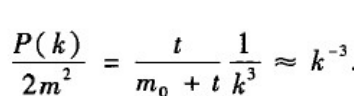
上式表明,P(k)/2m 2 ^2 2的取值与m无关。总是近似为k − 3 ^{-3} −3。
2.2 主方程方法
平均场分析毕竟是一种近似分析方法,得到的度分布的幂指数是正确的,但是度分布的系数并不准确。下面我们将针对更为一般的模型基于主方程方法给出的精确计算。
BA网络平均路径长度和聚类系数的推导由于涉及较深的数学知识,这里只给出有关结果。BA网络的平均路径长度比网络规模的对数还要小;具体地说,当m≥2时有:
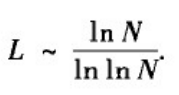
另一方面,当网络规模充分大时,BA网络并不具有明显的聚类特征;具体地说,BA网络的聚类系数满足:
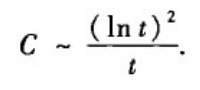
二、Price模型
1、模型描述
BA模型的度分布是幂指数固定为3的幂律分布,而许多实际的无标度网络的度分布的幂指数都是在2与3之间的。因此,我们希望能有一个幂指数可以在一定范围内调整的无标度网络模型。而这种模型居然在BA模型提出之前的30年就已经存在了。它就是Price模型。
Price有向网络模型构造算法:
(1)增长:从一个具有m 0 _0 0个孤立节点的网络开始,每次引入一个新的节点并且通过m条有向边指向m个已存在的节点上,这里m<=m 0 _0 0。
(2)累积优势:一个新节点有边指向一个已经存在的入度为k i i n ^{in}_i iin的节点i的概率满足如下关系:
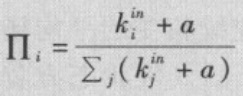
2、幂指数可调的入度分布
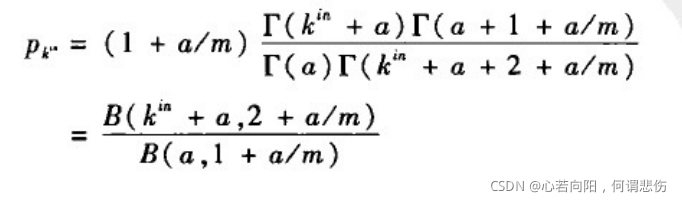
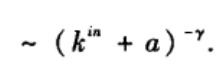
其中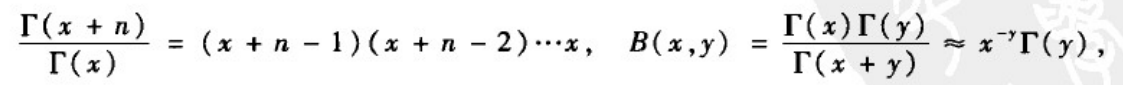
幂指数为:
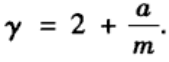
当k i n ^{in} in>>a时有:
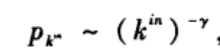
这表明Price网络模型的入度分布近似服从幂指数 λ \lambda λ=2 +a/m的幂律分布。如果a/m≤1,那么幂指数 λ \lambda λ∈(2,3],这意味着Price网络模型是一个非均匀的异质网络。随着a/m值的增加,Price网络模型的人度分布的均匀性也不断增加。因此,Price网络模型实际上是一个幕指数可调的幂律人度分布的网络模型。
3、幂指数可调的无向无标度网络
如果把Price模型中的每一条有向边都视为无向边,那么这样构成的无向网络中的节点i的度k i _i i与Price 模型中的节点i的出度m和人度k i i n _i^{in} iin 之间具有如下关系:k i _i i=k i i n _i^{in} iin +m。因此,基于Price模型的入度分布对应的无向网络的度分布为:
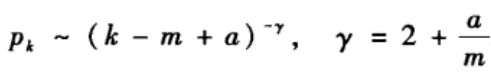
这样就得到了幂指数在(2, ∞ \infty ∞)范围内可调的具有幂律度分布的无向网络。
BA模型可以视为Price模型在取m=a时的特例。
4、优先连接机制的计算机实现
Price模型的计算机实现算法:
(1)给定一个具有m 0 _0 0个节点的初始强连通网络。把每一条边所指向的节点的编号添加到数组Array中。
(2)给定参数p ∈ \in ∈[0,1]。对于t=1,2,,,N-m 0 _0 0,执行如下操作:
1)生成一个完全随机数r ∈ \in ∈[0,1);
2)如果r<p,那么就完全随机的在数组Array中选择一个元素。
3)如果r>=p,那么就完全随机的选择一个节点。
4)执行步骤1)到3)m次后,添加从新加入节点指向选定的m个节点的m条有向边,并把这m个节点的编号添加到数组Array中。
5、节点复制模型
在优先连接的计算机实现中,由于数组Array是由网络中每个节点所指向的邻居节点的编号组成的,因此完全随机地在数组Array中选取一个元素等价于如下操作:完全随机地选择一个已有节点,然后再完全随机地选择该节点所指向的一个邻居点。
也就是说,在一定程度上(由参数p决定),新加入节点倾向于模仿(复制)网络中已有节点的行为。这种节点复制模式导致“富者更富”:某个节点如果已经受到很多关注,那么今后就更有可能受到更多的关注。我们可以把参数p视为复制概率:p值越大,意味着新加入的节点越倾向于复制已有节点的行为,从而导致更为显著的富者更富。
节点复制模型构造算法如下:
(1)增长:从一个具有m 0 _0 0个孤立节点的网络开始,每次引入一个新的节点并且通过m条有向边指向m个已存在的节点上,这里m≤m 0 _0 0。
(2)节点复制:给定一个参数p∈[0,1],按照如下方式选择已有节点,并添加从新节点指向该已有节点的有向边:
1)生成一个完全随机数r ∈ \in ∈[0,1);
2)如果r<p,那么就完全随机的选择一个节点,然后再完全随机的选取该节点所指向的一个邻居节点。
3)如果r>=p,那么就完全随机的选择一个节点。
4)执行步骤1)到3)m次,并避免重复选择节点。
三、无标度网络模型的推广
BA模型把实际复杂网络的无标度特性归结为增长和优先连接这两个非常简单明了的机制,这很好地体现了科学研究中的从复杂现象提取简单本质的特点。但是在BA模型中,越老的节点具有越高的度;换句话说,后来者不可能居上。然而,在许多实际网络中,节点的度及其增长速度并非只与该节点的年龄有关,还与节点的内在属性相关。
接下来介绍BA模型的两种推广:一种是考虑到节点之间具有不同的竞争能力的适应度模型,另一种是基于局域世界优先连接的网络模型。
1、适应度模型
适应度模型构造算法:
(1)增长:从一个具有m 0 _0 0个节点的连通网络开始,每次引入一个新的节点并且连到m个已存在的节点上,这里m≤m 0 _0 0。
(2)优先连接:一个新节点与一个已经存在的节点i相连接的概率与节点i的度k i _i i和适应度η i _i i之间满足如下关系:
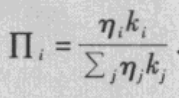
可以看出,适应度模型与BA无标度模型的区别在于,适应度模型中的优先连接概率与节点的度和适应度之积成正比,而不是仅与节点的度成正比。
2、局部世界演化网络模型
局部世界演化模型是在BA模型的基础上基于在诸多实际的复杂网络中存在着局域世界考虑的。
局域世界演化模型构造算法:
(1)增长:网络初始时有m 0 _0 0个节点和e 0 _0 0条边。每次新加人一个节点和附带的m条边。
(2)局域世界优先连接:随机地从网络已有的节点中选取M个节点(M≥m),作为新加入节点的局域世界(LW)。新加入的节点根据优先连接概率来选择与局域世界中的m个节点相连,其中LW由新选的M个节点组成:
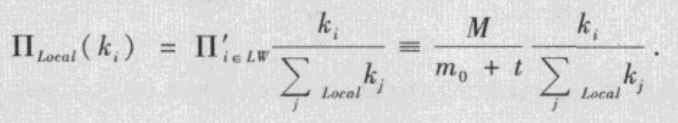
在每一时刻,新加入的节点从局域世界中按照优先连接原则选取m个节点来连接,而不是像BA无标度模型那样从整个网络中来选择。构造一个节点的局域世界的法则根据实际的局域连接而不同,上述模型中只考虑了随机选择的简单情形。
显而易见,在t时刻,m≤M≤m 0 _0 0+t,因此,上述局域世界演化网络模型有两个特殊情形:M=m和M=t+m 0 _0 0。
(1)特殊情形1:M=m
这时,新加入的节点与其局域世界中所有的节点相连接,这意味着在网络增长过程中,优先连接原则实际上已经不发挥作用了。这等价于BA无标度网络模型中只保留增长机制而没有优先连接时的特例。此时,第i个节点的度的变化率为
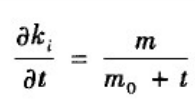
网络度分布服从指数分布:
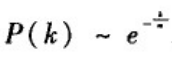
(2)特殊情形2:M=t+m 0 _0 0
在这种特殊情形,每个节点的局域世界其实就是整个网络。因此,局域世界模型此时完全等价于BA无标度网络模型。
四、鲁棒性与脆弱性
对于给定的一个网络,每次从该网络中移走一个节点,也就同时移走了与该节点相连的所有的边,从而有可能使得网络中其他节点之间的一些路径中断。如果在节点i和节点j之间有多条路径,中断其中的一些路径就可能会使这两个节点之间的距离d i j _{ij} ij增大,从而整个网络的平均路径长度L也会增大。如果节点i和j之间的所有路径都被中断,那么这两个节点之间就不再连通了。如果在移走少量节点后网络中的绝大部分节点仍是连通的,那么就称该网络的连通性对节点故障具有鲁棒性。
考虑两类节点去除策略:一是随机故障策略,即完全随机地去除网络中的一部分节点;二是蓄意攻击策略,即从去除网络中度最高的节点开始,有意识地去除网络中一部分度最高的节点。
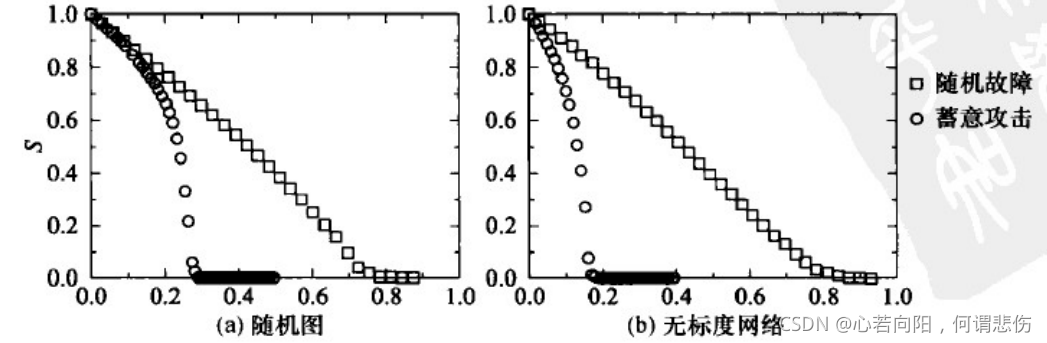
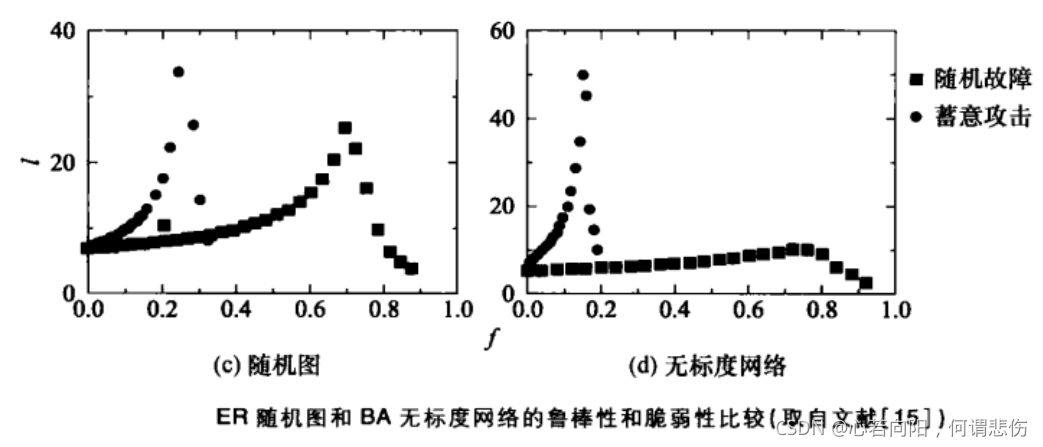
从上图得知无标度网络对随机节点故障具有极高的鲁棒性;但对蓄意攻击具有极高的脆弱性,只要有意识的去除网络中极少量度大的节点就会对整个网络的连通性产生很大的影响。
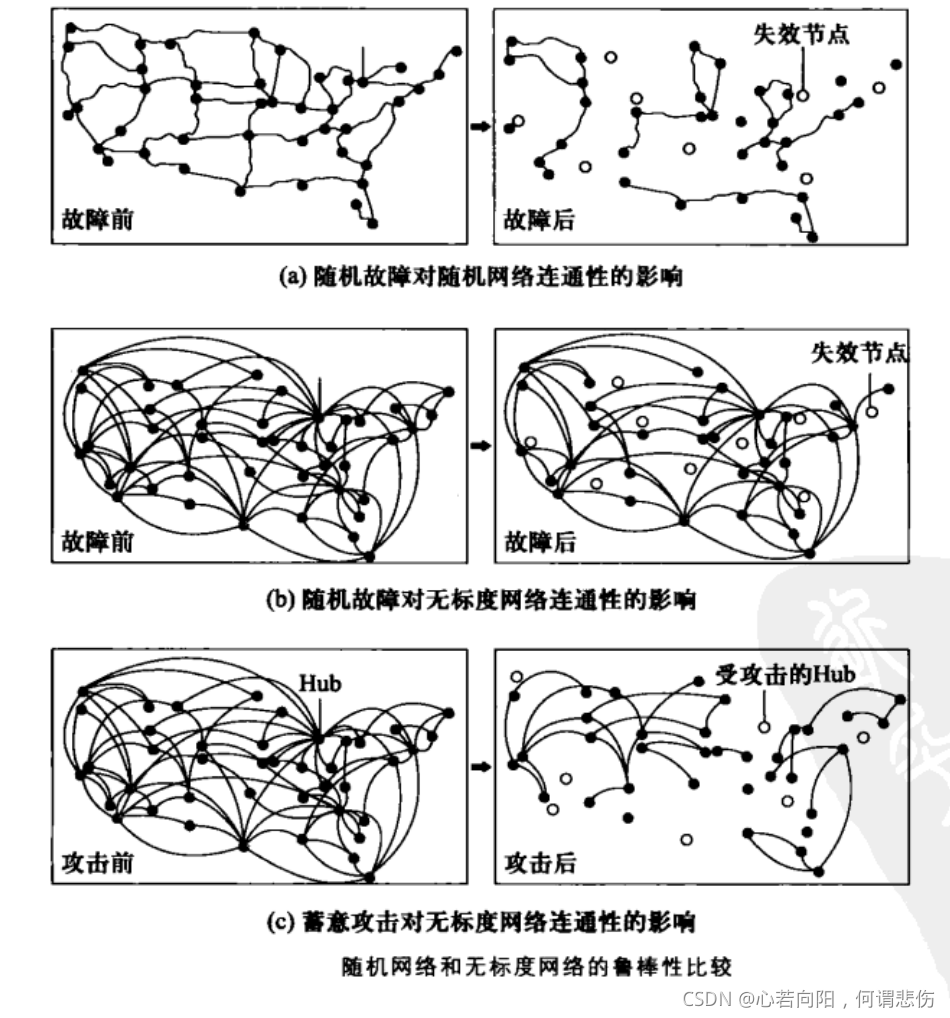
上图形象的比较了随机网络和无标度网络的鲁棒性。