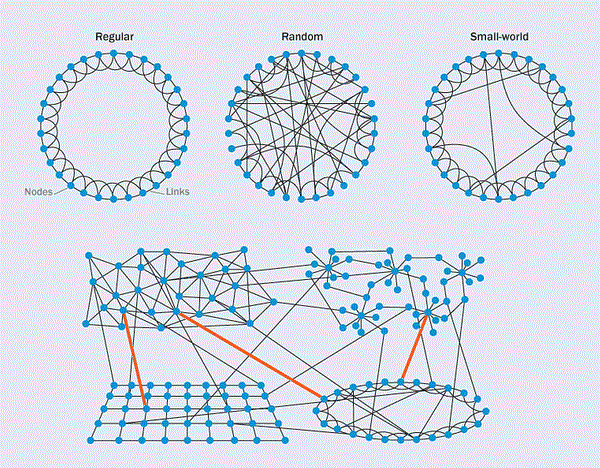
复杂网络（Complex Network），是指具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络。特征：小世界、集群即集聚程度的概念、幂律的度分布概念。

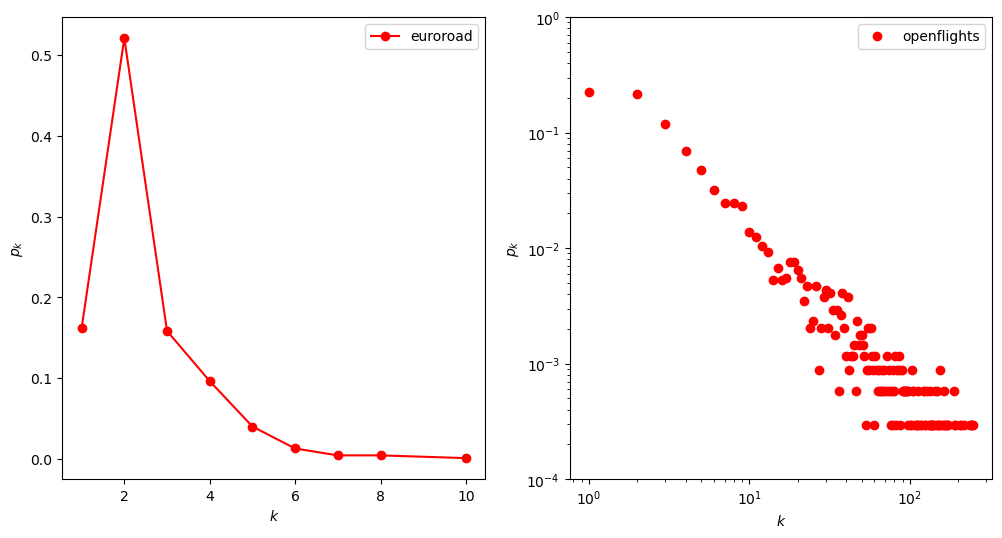
BA模型是由巴拉巴西（Albert-László Barabási）与阿尔伯特（Réka Albert）提出的无标度网络模型。在此之前，大多数网络被想当然的认为是随机的，因此连接度分布可以近似用泊松分布来表示，而巴拉巴西与其学生阿尔伯特、郑浩雄通过对万维网度分布测量的结果却显示万维网度分布服从幂律分布，存在枢纽节点（拥有大量链接的节点）。也许万维网是特别的，巴拉巴西研究组进而又分析了两个网络系统——IBM计算机芯片布线图与好莱坞演员数据库，结果其度分布均遵循幂律分布。

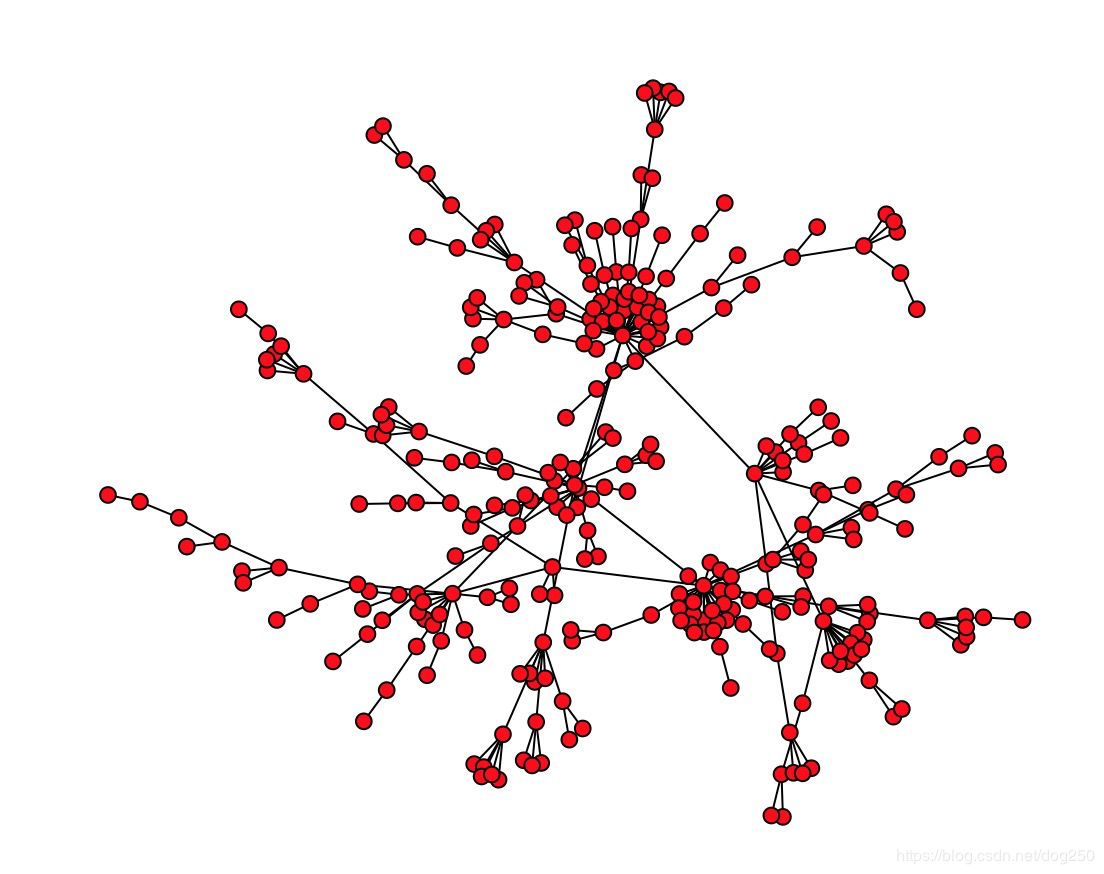
仿真实现BA无标度网络，使用的是MATLAB

clc, clear
m0=input('请输入未增长前的网络节点个数m0: ');
m=input('请输入每次引入新节点时新生成的边数m： ');
N=input('请输入增长后的网络节点总数N： ');
disp('初始网络时m0个节点的连接情况：1表示都是孤立点；2表示构成完全图；3表示随机连接一些边');
se=input('请选择初始网络情况1，2或3： ');
if m>m0disp('输入参数m不合法'); return;
end
x=100*rand(1,m0); y=100*rand(1,m0);  %构造初始用于画图的m0个节点坐标
if se==1A=zeros(m0);
elseif se==2A=ones(m0); A(1:m0+1:m0^2)=0; %对角线元素置0
elseA=zeros(m0); B=rand(m0); B=tril(B); %截取下三角元素A(B<=0.1)=1; %按照概率0.1进行连边A=A+A';  %构造完整的邻接矩阵
end 
for k=m0+1:Nx(k)=100*rand; y(k)=100*rand; %生成用于当前节点画图的坐标p=(sum(A)+1)/sum(sum(A)+1); %计算所有节点的连接概率pp=cumsum(p); %求累积分布A(k,k)=0;   %加入新的连边之前，邻接矩阵扩充维数ind=[]; %新节点所连节点的初始集合while length(ind)<mjj=find(pp>rand); jj=jj(1); %用赌轮法选择连边节点的编号ind=union(ind,jj); %使用union保证选择的节点不重复endA(k,ind)=1; A(ind,k)=1; %构造加边以后新的邻接矩阵
end
plot(x,y,'ro','MarkerEdgeColor','g','MarkerFaceColor','r','markersize',8);
hold on, A2=tril(A); [i,j]=find(A2); %找邻接矩阵下三角元素的非零元素
for k=1:length(i)plot([x(i(k)),x(j(k))],[y(i(k)),y(j(k))],'linewidth',1.2)
end
deg=sum(A);  %计算邻接矩阵的列和,即各节点的度
ave_degree=sum(deg)/N;  %计算平均度
figure, bar([1:N],deg); %画各节点度的柱状图
title('网络图各节点度大小');
xlabel('$v_{i}$','Interpreter','Latex'), ylabel('$k$','Interpreter','Latex')
degrange=minmax(deg); %求度的取值范围
pinshu=hist(deg,[degrange(1): degrange(2)]);%求度取值的频数
df=pinshu/N; %求度的频率分布
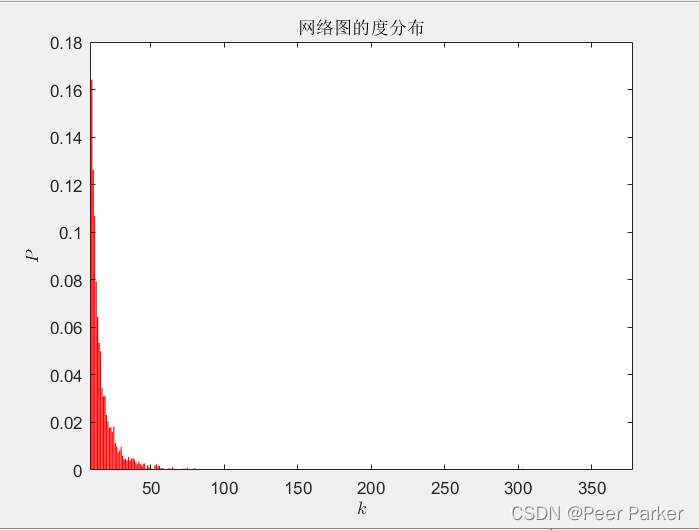
figure, bar([degrange(1):degrange(2)],df,'r')  %画度分布柱状图
title('网络图的度分布');
xlabel('$k$','Interpreter','Latex'), ylabel('$P$','Interpreter','Latex')

结果展示

 赶紧放假吧，好累！！！