networkx学习(五)无标度网络
参考:参考来源,《巴拉巴西网络科学》
无标度网络:
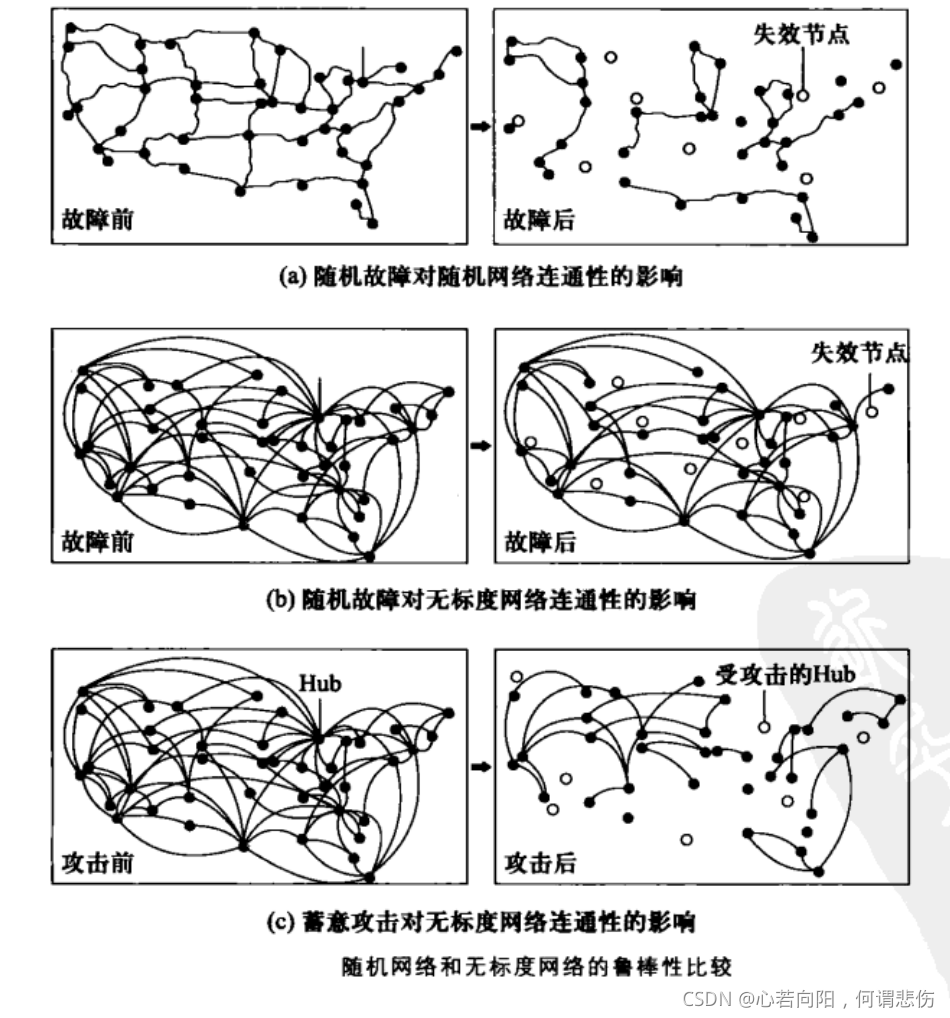
对于随机网络和规则网络,度分布区间非常狭窄,大多数节点都集中在节点度均值< k >的附近,说明节点具有同质性,因此< k >可以被看作是节点度的一个特征标度。而在节点度服从幂律分布的网络中,大多数节点的度都很小,而少数节点的度很大,说明节点具有异质性,这时特征标度消失。这种节点度的幂律分布为网络的无标度特性。
1.无标度性质
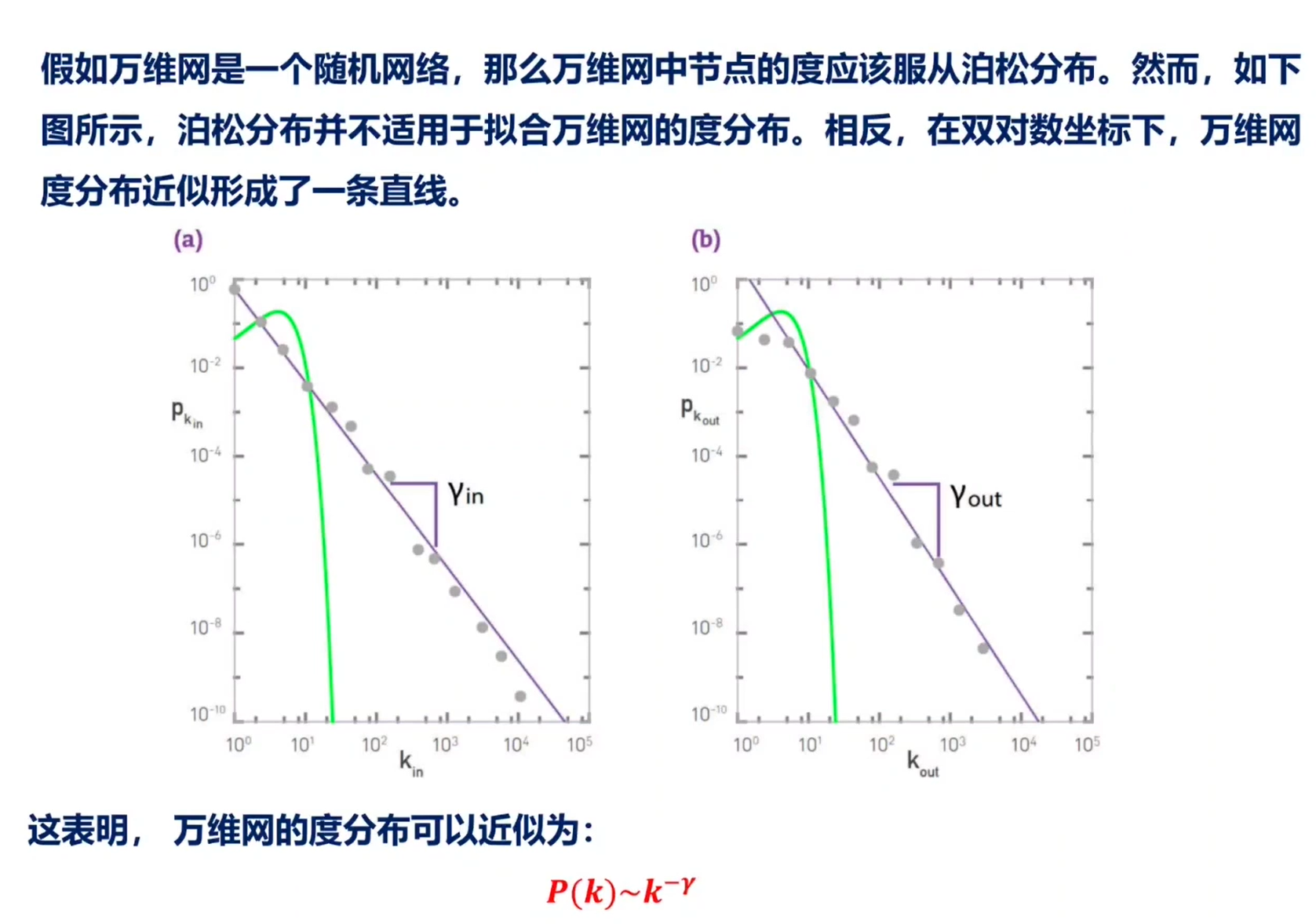
在万维网的连接图背后似乎隐藏着大量的随机性。然而,仔细观察就会发现,万维网地图和随机网络之间存在一些令人费解的差异。实际上,在随机网络中,高度连接的节点——枢纽节点,是几乎不可能出现的。相比之下,万维网中同时存在大量度很小的节点和少数几个枢纽节点——拥有链接数异常多的节点。


实践一
1、道路网络和航空网络的度分布
# 导入库
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd# 加载euroroad数据集
df1 = pd.read_csv("euroroad.csv")
G1 = nx.from_pandas_edgelist(df1, 'source', 'target', create_using = nx.Graph())# 加载openflights数据集
df2 = pd.read_csv("openflights.csv")
G2 = nx.from_pandas_edgelist(df2, 'source', 'target', create_using = nx.Graph())print(len(G1.nodes()), len(G2.nodes()))
# 定义求度分布的函数
def get_pdf(G):all_k = [G.degree(i) for i in G.nodes()]k = list(set(all_k)) # 获取所有可能的度值N = len(G.nodes())Pk = []for ki in sorted(k):c = 0for i in G.nodes():if G.degree(i) == ki: c += 1 Pk.append(c/N) return sorted(k), Pk
deg1 = [G1.degree(i) for i in G1.nodes()]
deg2 = [G2.degree(i) for i in G2.nodes()]k1, Pk1 = get_pdf(G1)
k2, Pk2 = get_pdf(G2)plt.figure(figsize=(12,6))plt.subplot(121)
plt.plot(k1, Pk1, 'ro-', label='euroroad')
plt.legend(loc=0)
plt.xlabel("$k$")
plt.ylabel("$p_k$")plt.subplot(122)
plt.plot(k2, Pk2, 'ro', label='openflights')
plt.legend(loc=0)
plt.xlabel("$k$")
plt.ylabel("$p_k$")
plt.ylim([1e-4,1])
plt.xscale("log")
plt.yscale("log")
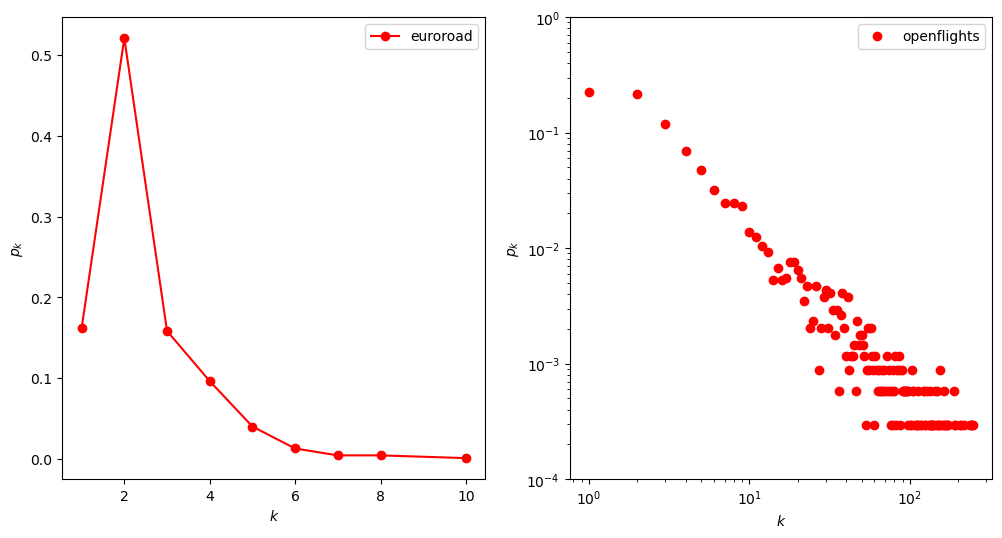
2、对于航空网络,粗略拟合度分布
from scipy import optimizedef fit_line(x, a, b):return a * x + b