无标度网络的C++代码实现

前言

上一篇文章中给出了ER随机网络的C++代码实现，这篇文章让我们来说一下另一个科研中用的非常广泛的网络——无关联无标度网络，即SF, UCM网络模型。

背景

BA无标度网络的发展及算法

无标度网络的发展要追溯到20世纪末，由Barabási和Albert提出的BA无标度网络模型，他们说明了一些大型网络，例如万维网和基因网络，其度分布满足幂律性它是一个度分布满足幂律分布 𝑃 (𝑘) ∼ 𝑘-3 的网络。 BA 的构建与随机网络不同，它是一种不断增长的网络，并且它新增加的节点并不是完全随机的连接向原网络中的任意节点，而且存在一种优先依附的关系。BA无标度网络的具体生成方法如下：
1. 给定网络总体大小 𝑁，从一个三元组或一个存在 𝑚0 个节点的简单图开始。

2. 网络增长：每次增加一个节点，并与原有网络中的 𝑚 个节点进行连接。连接满足优先性，且 𝑚 ≤ 𝑚0。

3. 优先依附：新节点与原有节点 𝑖 会优先考虑原有网络中度较大的节点，节点 𝑖连接到原网络中其它节点的概率为：。

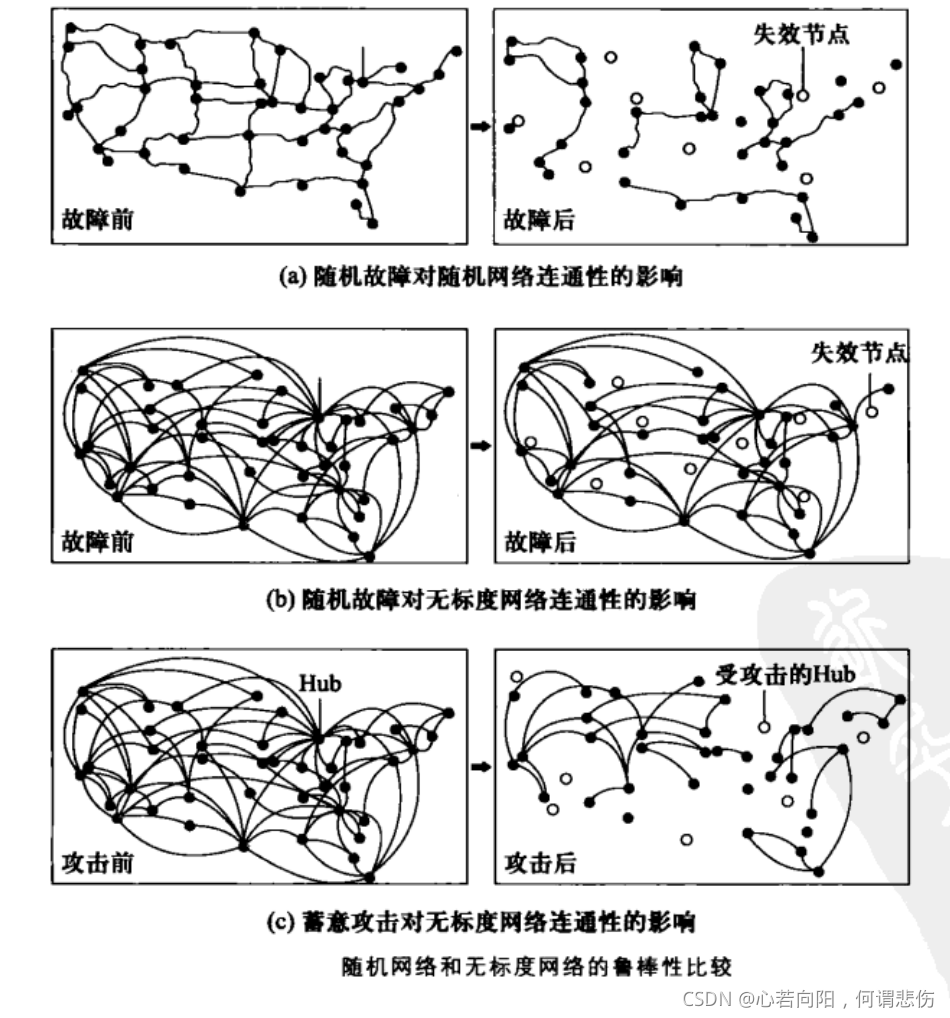
BA 网络由于优先依附的存在，实际上是一个同构 (关联) 网络，通常用来描述“富人更富”、马太效应及累计优势等现象，这也是它备受科学家青睐的原因。

无关联无标度网络的发展及算法

此外，无标度网络发展出了另一种形式，它不单解决了 BA 网络幂律指数固定为3的问题，同时去掉了优先依附效应，构建出了一种无关联无标度网络。 Michele Catanzaro 和 Marián Boguñá 等人给出的构建无关联配置模型的算法可以描述为：

1. 给定网络的大小 𝑁，同时根据给出的网络度分布为每个节点分配度，并且限制节点度，其中 m 为网络中的最小度，而为网络最大度，取值为正整数。

2. 节点的度意味着节点拥有个存根 (stubs)，将节点 1 ∼ 𝑁 号的存根进行排序，每次随机选取两个存根进行连边，直到所有存根选取完，就构建了网络。注意，无关联配置模型的构建应当保证存根总数量为偶数，存根的选择需避免网络产生重连边与自连边。同时，若出现剩余几个存根之间互有连接时，应当放弃本次网络构建，从第一步重新开始。

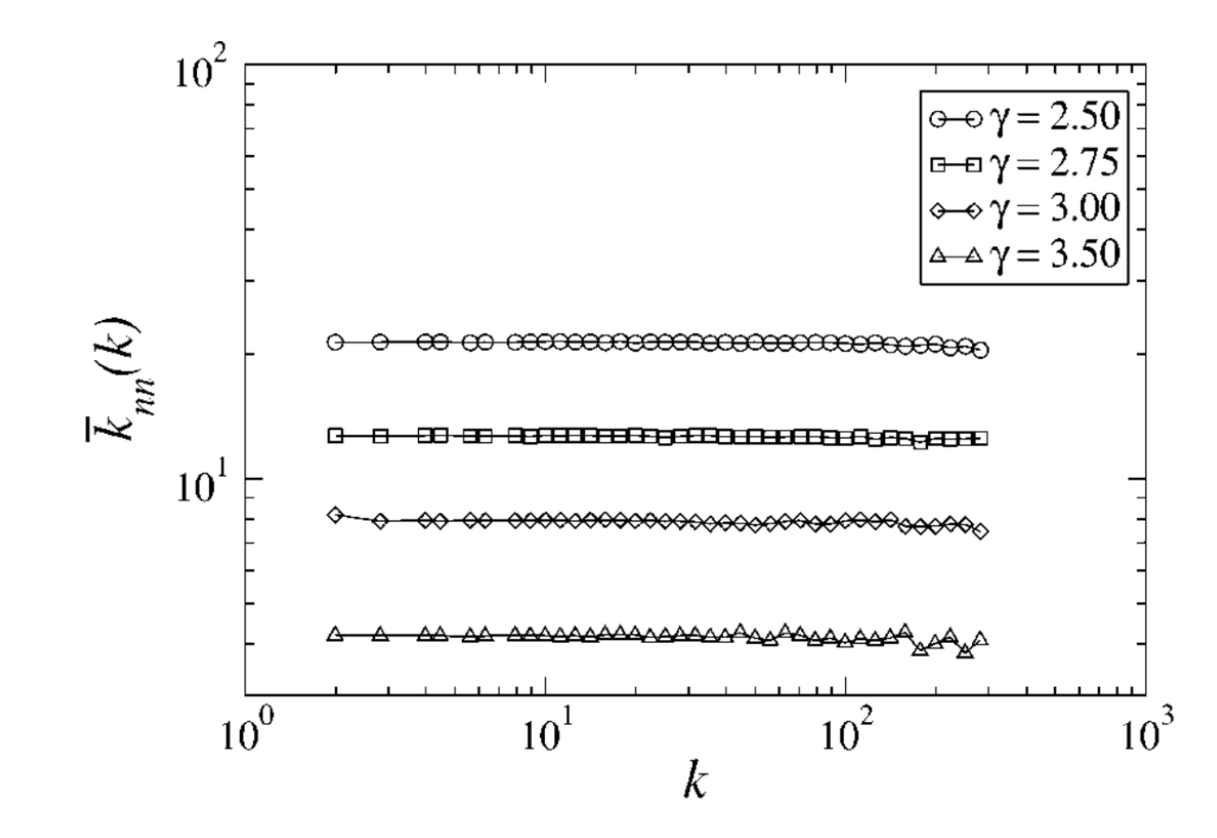
无标度网络顾名思义，其网络节点之间的度呈现无关联性。同样，网络的性质不做过多阐述，复杂网络的任意一本书中都有很详细的描述。

C++代码实现

BA无标度网络

#include <iostream>
#include <ctime>
#include <stdlib.h>
#include <fstream>
#include <cmath>
#include "mt19937ar.c"
#include <vector>
#include <algorithm>using namespace std;int main()
{int Network_Size = 10000;double r;                                                   //用来判断连边的随机数long int m0;cout << "初始连通网络的节点数m0:";cin >> m0;                                                  //取m0个点构成连通网络long int m;                                                 //新节点连接旧节点的m条边数cout << "请输入增加的节点所连接旧节点的边数:";cin >> m;if(m > m0){cout << "m不能大于m0，输入错误";exit(1);}long int t = Network_Size - m0;cout << "步长t = " << t << endl;vector<double> sequence(Network_Size,0);vector<double> degree(Network_Size,0);vector<double> statistics(Network_Size,0);double Sum_degree = 0;vector<double> Probability_degree(Network_Size,0);double probability_degree_distribute = 0;vector<double> Probability_Sum(Network_Size+1,0);vector<vector<int> > adjlist(Network_Size);ofstream outfile_BA_adjacent_matrix;       //输出邻接矩阵到文本文件ofstream outfile_BA_degree;                //输出度分布到文本文件outfile_BA_adjacent_matrix.open("BA_adjacent_matrix.txt");outfile_BA_degree.open("BA_degree.txt");unsigned long idum;idum=(unsigned long)time(NULL);init_genrand(idum);for(int i = 0; i < m0; i++){for(int j = i + 1; j < m0; j++){if(i != j){adjlist[i].push_back(j);degree[i]++;adjlist[j].push_back(i);degree[j]++;}}}for(int i = 0; i < m0; i++){for(int j = 0; j < adjlist[i].size(); j++){cout << adjlist[i][j] << ' ';}cout << endl;}Sum_degree = m0 * (m0 - 1);double temp = 0;for(int i = 0; i < m0; i++)               //m0个节点组成的联通网络中每个节点的优先概率{Probability_degree[i] = degree[i]/Sum_degree;temp = temp + Probability_degree[i];Probability_Sum[0] = 0;Probability_Sum[i + 1] = temp;Probability_Sum[m0] = 1;}for(int i = m0; i < Network_Size; i++)   //增长{int u = m;for(;;){if(u == 0){break;}r = genrand_real2();int judge = 0;for(int p = 0; p < i; p++){if(r < Probability_Sum[p + 1] ){for(int k = 0; k < adjlist[p].size(); k++){if(adjlist[p][k] == i){judge = 1;break;}}if(judge == 1){break;}adjlist[p].push_back(i);degree[p]++;adjlist[i].push_back(p);degree[i]++;Sum_degree = Sum_degree + 2;u--;double Sum = 0;                         //更新for(int w = 0; w <= i; w++){Probability_degree[w] = degree[w]/Sum_degree;Sum = Sum + Probability_degree[w];Probability_Sum[0] = 0;Probability_Sum[w + 1] = Sum;Probability_Sum[i] = 1;}break;}}}}for(int i = 0; i < NetWork_Size; i++){outfile_BA_adjacent_matrix << '\t' << endl;for(int j = 0; j < adjlist[i].size(); j++){outfile_BA_adjacent_matrix << adjlist[i][j] <<' ';}outfile_BA_adjacent_matrix << endl;}for(int i = 0; i < Network_Size; i++){sequence[i] = i;for(int j = 0; j < Network_Size; j++){if(sequence[i] == degree[j]){statistics [i]++;}}probability_degree_distribute = (statistics[i]) / Network_Size;outfile_BA_degree << sequence[i] << '\t' << probability_degree_distribute << endl;}return 0;
}

无关联无标度网络

#include <iostream>
#include <ctime>
#include <stdlib.h>
#include <fstream>
#include <cmath>
#include "mt19937ar.c"
#include <vector>
#include <algorithm>using namespace std;int Network_Size = 1000;        //网络规格int edge = 0;                   //边的数量int main()
{double random_number;int m0 = 5;                     //网络中的最小度double r = 3.5;                          //幂double Sum = 0;double degree_Sum = 0;vector<int> degree(Network_Size);vector<double> probability_degree_distribution(Network_Size);vector<double> Probability_Sum(Network_Size);vector<vector<int> > adjlist(Network_Size);unsigned long idum;idum = (unsigned long)time(NULL);init_genrand(idum);ofstream outfile_UCM_adjacent_matrix;       //输出邻接矩阵到文本文件outfile_UCM_adjacent_matrix.open("UCM_adjlist.txt");ofstream out_degree;out_degree.open("UCM_degree.txt");for(int i = m0; i < Network_Size; i++){probability_degree_distribution[i] = pow(i,-r);Sum = Sum + probability_degree_distribution[i];}for(int i = m0; i < Network_Size; i++)                        //归一化{probability_degree_distribution[i] = probability_degree_distribution[i]/Sum;}double temp_1 = 0;for(int i = m0; i < Network_Size; i++){temp_1 = temp_1 + probability_degree_distribution[i];Probability_Sum[i] = temp_1;}for(int i = 0; i < Network_Size; i++){random_number = genrand_real2();for(int j = m0; j < Network_Size; j++){if(random_number < Probability_Sum[m0]){degree[i] = m0;break;}else if(random_number > Probability_Sum[(int)sqrt(Network_Size)]){degree[i] = (int)sqrt(Network_Size);break;}else if((random_number > Probability_Sum[j] && random_number < Probability_Sum[j + 1]) && Probability_Sum[j+1] <= Probability_Sum[(int)sqrt(Network_Size)]){degree[i] = j;break;}}}for(int i = 0; i < Network_Size; i++){degree_Sum = degree_Sum + degree[i];}if((int)degree_Sum % 2 != 0){degree[0]++;degree_Sum++;}vector<int> stabs(degree_Sum);int k = 0;for(int i = 0; i < Network_Size; i++){for(int j = 0; j < degree[i]; j++){stabs[k] = i;k++;}}int degree_Sum2 = degree_Sum;sort(stabs.begin(),stabs.end(),greater<int>());for(;;){int judge = 0;if(degree_Sum2 == 0){break;}int i = genrand_int32() % degree_Sum2;int j = genrand_int32() % degree_Sum2;if(stabs[i] == stabs[j]){continue;}if(stabs[i] != stabs[j]){for(int k = 0; k < adjlist[stabs[i]].size(); k++){if(adjlist[stabs[i]][k] == stabs[j]){judge = 1;break;}}if(judge == 1){continue;}else{adjlist[stabs[i]].push_back(stabs[j]);adjlist[stabs[j]].push_back(stabs[i]);stabs[i] = stabs[degree_Sum2-1];stabs[j] = stabs[degree_Sum2-2];degree_Sum2 = degree_Sum2 - 2;}}}for(int i = 0; i < Network_Size; i++){out_degree << degree[i] << endl;}for(int i = 0; i < Network_Size; i++){outfile_UCM_adjacent_matrix << i << '\t';for(int j = 0; j < adjlist[i].size(); j++){outfile_UCM_adjacent_matrix << adjlist[i][j] << ' ';}outfile_UCM_adjacent_matrix << endl;}return 0;
}

注意："mt19937ar.c"为高精度随机种子生成器，也可以将替换为C++自带的随机种子；"mt19937ar.c"在上一篇ER随机网络的文章中给出了用法与代码。同时，无关联无标度网络的代码中并没有去除最后剩下几条边互相不能链接的情况，这时可能会造成死循环，通常我的做法是再生成一次网络，或者可以在代码中再添加一层循环，来判断是否出现这种情况，但这样就降低了生成效率。