通过点拟合圆
- 三点确定一个圆
- 多点拟合一个圆
三点确定一个圆
参考代码: matlab空间三点求圆心
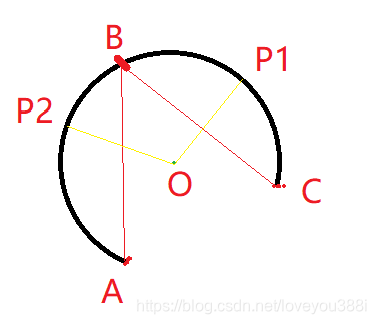
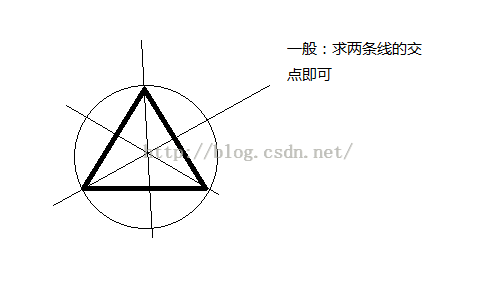
代码中使用的算法原理是:三个点确定两个线段,圆心位于两个线段的中垂线上,所以圆心坐标符合两个中垂线的性质,具体推导如下(我的推导过程和原文中的稍有区别,我算出d,原文算出k,思路一致):

代码转自博客: matlab空间三点求圆心
function p = CircleCenter(p1, p2, p3)
% CircleCenter(p1, p2, p3) 根据三个空间点,计算出其圆心
% p1,p2,p3:三个空间点% 圆的法向量pf= cross(p1-p2, p1-p3);if any(pf == 0)error('三个点不能共线!!');end% 两条线段的重点,之后需要求中垂线p12 = (p1 + p2)/2;p23 = (p2 + p3)/2;% 求两条线的中垂线p12f = cross(pf, p1-p2);p23f = cross(pf, p2-p3);% 求在中垂线上投影的大小ds = ( (p12(2)-p23(2))*p12f(1) - (p12(1)-p23(1))*p12f(2) ) / ( p23f(2)*p12f(1) - p12f(2)*p23f(1) );% 得出距离p = p23 + p23f .* ds;end
多点拟合一个圆
在空间中,我们有时候需要多个点去拟合一个最佳的圆。
转自博客 最小二乘法拟合圆




原博客附加代码:
/*** 最小二乘法拟合圆* 拟合出的圆以圆心坐标和半径的形式表示* 此代码改编自 newsmth.net 的 jingxing 在 Graphics 版贴出的代码。* 版权归 jingxing, 我仅仅是搬运工外加一些简单的改动工作。*/
typedef complex<int> POINT;
bool circleLeastFit(const std::vector<POINT> &points, double ¢er_x, double ¢er_y, double &radius)
{center_x = 0.0f;center_y = 0.0f;radius = 0.0f;if (points.size() < 3){return false;}double sum_x = 0.0f, sum_y = 0.0f;double sum_x2 = 0.0f, sum_y2 = 0.0f;double sum_x3 = 0.0f, sum_y3 = 0.0f;double sum_xy = 0.0f, sum_x1y2 = 0.0f, sum_x2y1 = 0.0f;int N = points.size();for (int i = 0; i < N; i++){double x = points[i].real();double y = points[i].imag();double x2 = x * x;double y2 = y * y;sum_x += x;sum_y += y;sum_x2 += x2;sum_y2 += y2;sum_x3 += x2 * x;sum_y3 += y2 * y;sum_xy += x * y;sum_x1y2 += x * y2;sum_x2y1 += x2 * y;}double C, D, E, G, H;double a, b, c;C = N * sum_x2 - sum_x * sum_x;D = N * sum_xy - sum_x * sum_y;E = N * sum_x3 + N * sum_x1y2 - (sum_x2 + sum_y2) * sum_x;G = N * sum_y2 - sum_y * sum_y;H = N * sum_x2y1 + N * sum_y3 - (sum_x2 + sum_y2) * sum_y;a = (H * D - E * G) / (C * G - D * D);b = (H * C - E * D) / (D * D - G * C);c = -(a * sum_x + b * sum_y + sum_x2 + sum_y2) / N;center_x = a / (-2);center_y = b / (-2);radius = sqrt(a * a + b * b - 4 * c) / 2;return true;
}
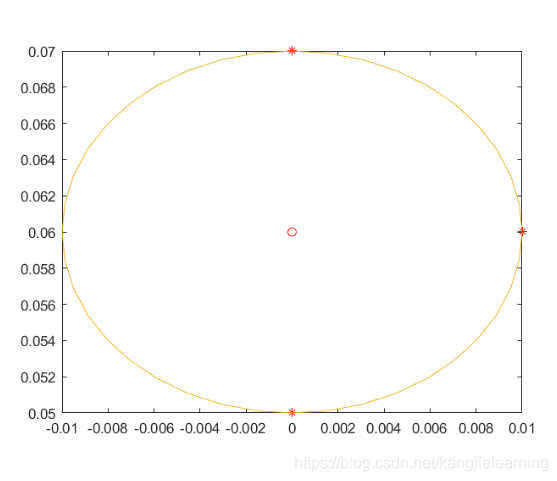
作者给出的效果图: