资源下载地址:linux内核hook系统调用execve函数-Linux文档类资源-CSDN下载
(已在内核为 4.19.0-amd64-desktop版本uos编译通过,并成功达到目的)
在Linux系统中,用户层程序无法直接控制系统内核,只能通过系统调用。
一般调用顺序为:
用户进程->execve()->syscall()->stub_execve()->sys_execve()-> do_execve().....
本文章使用的是国产uos-Linux,内核为 4.19.0-amd64-desktop
使用strace命令,可以查看进程的系统调用(以deepin-calculator这个进程为例):

可见第一行即使用了execve系统调用。
那么,我们可以在内核中对execve函数进行hook,加入你想干的事情(比如让他打不开,又或者做一些邪恶的事情~),这里我们来让系统无法使用dpkg命令,也就是整个系统现在装不了也卸载不了软件了~~
(1)函数声明
typedef asmlinkage long (*m_sys_call_ptr_t)(const struct pt_regs *);static m_sys_call_ptr_t *psys_call_table;m_sys_call_ptr_t old_execve ; (2)获取系统调用地址
psys_call_table = (m_sys_call_ptr_t *)kallsyms_lookup_name("sys_call_table");(3)替换系统调用
disable_write_protect();old_execve = psys_call_table[__NR_execve];psys_call_table[__NR_execve] = HookGetExecves;enable_write_protect(); 注意这里替换的时候需要先对内核代码段打patch,也就是对开启内核代码段的保护(CR0),替换完毕后再关闭:
//关闭内存写保护
void disable_write_protect(void) { write_cr0(read_cr0() & (~0x10000)); }
// 开启内存写保护
void enable_write_protect(void) { write_cr0(read_cr0() | 0x10000); }(4)自定义hook函数,做你想做的事情
这里,我直接让deep-calculator起不来,无法打开
asmlinkage long HookGetExecves(const struct pt_regs * regs)
{char __user *filename = (char *)regs->di;char user_filename[NAME_MAX] = {0};long copied = strncpy_from_user(user_filename,filename,NAME_MAX);//printk("%s %s %d %d\n",__func__,user_filename,copied, NAME_MAX);if((strcasecmp(user_filename,"/usr/bin/dpkg")==0)){const char * const *argv = (const char *const *)regs->si;get_user_cmdline(argv, user_filename, NAME_MAX); // 解析出命令行,如果进程后面加了参数printk("====%s=====\n",user_filename); return -1; //这里让程序无法打开,直接退出}return old_execve(regs);
}(5)还原系统调用
disable_write_protect();psys_call_table[__NR_execve] = old_execve;enable_write_protect();最后,写个makefile编译一下,如图:
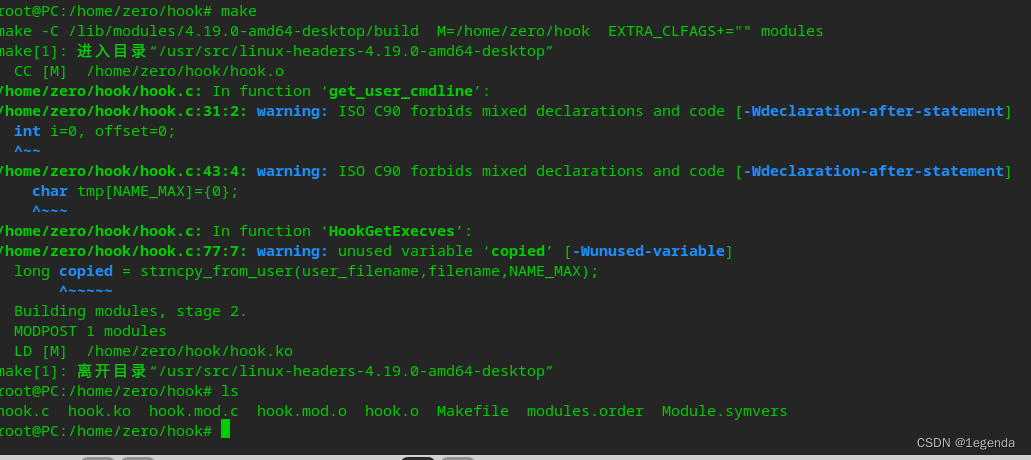
然后 sudo insmod hook.ko将编译好的内核模块,加载进去:
输入sudo dmesg --follow 可跟踪查看内核打印的消息,因为我们在代码中加了printk,现在来使用dpkg这个命令,看看有什么效果。

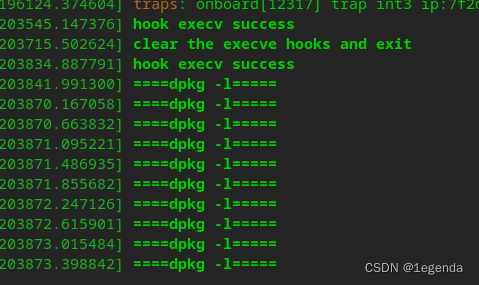
上面是使用dpkg -l 命令查看所有软件,发现现在dpkg已经用不了了。
然后下面的内核也打印出了printk里面的内容,即我们所调用的进程以及参数。
资源下载地址:linux内核hook系统调用execve函数-Linux文档类资源-CSDN下载