---

前言

本篇文章我们继续来研究一下execve这个系统调用，上篇文章已经讲解了前两个参数的意义了，那么这篇文章就来讲解一下第三个参数的具体含义。

一、execve的第三个参数

execve函数的第三个参数 envp 是一个字符串数组，用于传递给新程序的环境变量。

环境变量是操作系统提供给程序的一组全局变量，用于存储与系统环境相关的配置和信息。例如，PATH 环境变量指定了可执行程序所在的路径，HOME 环境变量指定了当前用户的家目录等。程序可以通过读取环境变量来获取系统相关的配置信息以及自定义的参数。

envp 参数是一个空指针结尾的字符串数组，每个元素都是一个以 "key=value" 形式表示的环境变量设置。例如，envp 数组可以包含类似以下的元素：

envp[0] = "PATH=/usr/local/bin:/usr/bin:/bin"
envp[1] = "HOME=/home/user"
envp[2] = "LANG=en_US.UTF-8"
...
envp[n] = NULL

在程序加载执行时，新程序会继承这些环境变量的设置，并且可以通过读取它们来获取相应的环境信息。

需要注意的是，envp 数组的最后一个元素必须是 NULL，用于表示环境变量列表的结束。

使用 envp 参数，可以在调用 execve 函数时传递自定义的环境变量给新程序。这允许程序在不同的执行环境中获得不同的配置。通过修改或添加环境变量，可以对新程序的行为进行定制和调整。

例如，可以根据需要设置自定义的环境变量，然后将其作为 envp 参数传递给 execve 函数，使新程序能够感知和使用这些自定义的环境变量。这样，新程序就可以根据环境变量的设置来执行不同的逻辑或采取不同的配置。
总结：

execve 函数的第三个参数 envp 是一个字符串数组，用于传递给新程序的环境变量。它允许自定义和传递环境变量给新程序，以便在程序加载执行时进行配置和定制。

这里对程序进行改进：
fork.c:

#include <stdio.h>
#include <sys/types.h>
#include <unistd.h>#define EXE "test"int main(void)
{int pid = 0;char* argv[3] = {EXE, "world", NULL};printf("begin\n");printf("now pid : %d\n", getpid());if((pid = fork()) != 0){//父进程}else{//子进程execve(EXE, argv, argv);}printf("end\n");return 0;
}

test.c:

#include <stdio.h>
#include <sys/types.h>
#include <unistd.h>int main(int argc, char** argv, char** envp)
{int i = 0;printf("argc :%d\n", argc);for(i = 0; i < argc; i++){printf("argv[%d] : %s\n", i, argv[i]);}printf("Hello World current pid :%d\n", getpid());i = 0;while(envp[i]){printf("envp[%d] :%s\n", i, envp[i]);i++;}return 0;
}

运行结果：

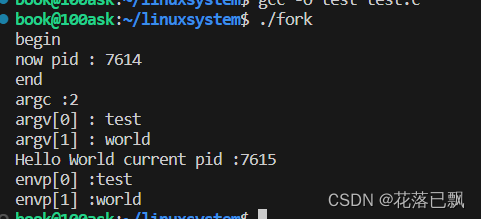
由运行结果可以看出子进程环境变量由父进程传递过来。

二、进程空间

这一张图片描述了进程的空间概要情况：

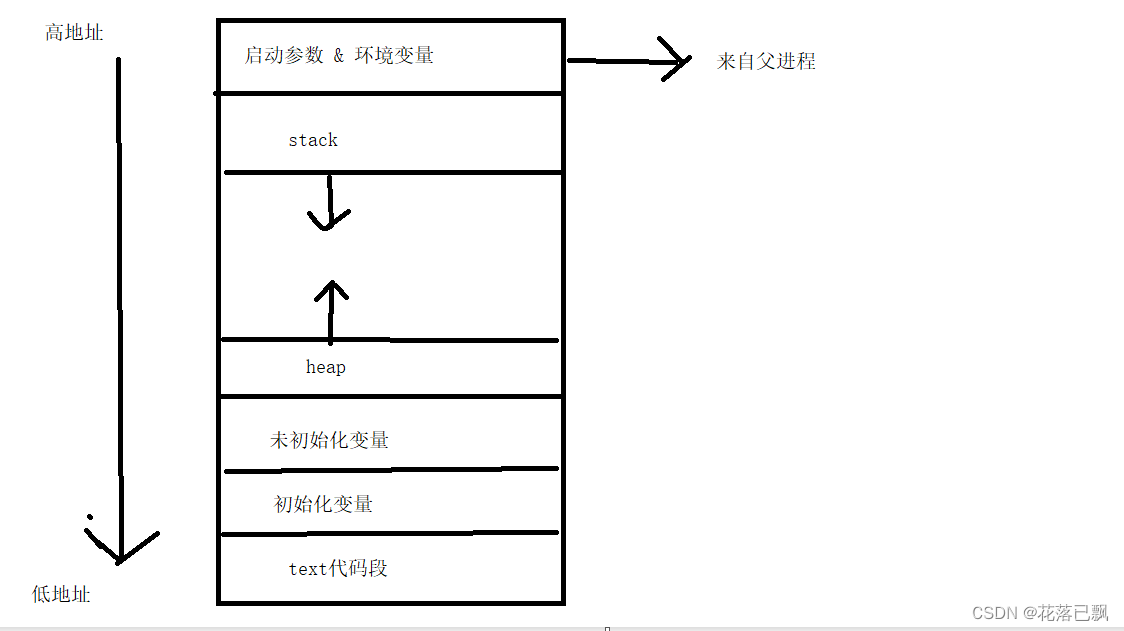
验证：

#include <stdio.h>
#include <malloc.h>static void Text(void)
{}int main(int argc, char** argv)
{int i = 0;int* p = (int*)malloc(4);static int uninitval;static int initval = 0;printf("argv[0] :%p\n", argv);//启动参数printf("i : %p\n", &i);//栈地址printf("p = %p\n", p);//堆地址printf("uninitval = %p\n", &uninitval);//未初始化变量printf("initval = %p\n", &initval);//初始化变量printf("Text = %p\n", Text);//代码段return 0;
}

运行结果：

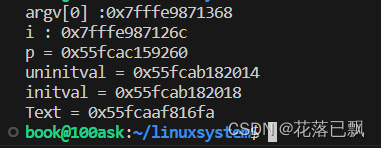
根据运行结果可以印证上图的结果。

三、命令行参数规范

1.由选项，选项值，操作数组成

2.选项由短横线(-)开始，选项名必须是单个字母或数字字符

3.选项可以有选项值，选项与选项值之间可用空格分隔(-o test -otest)

4.如果多个选项均无选项值，可合而为一(-a-b -c-abc)

5.既不是选项，也不能作为选项值的参数是操作数

6.第一次出现的双横线(–)用于结束所有选项，后续参数为操作数

getopt函数讲解：

getopt 是一个用于解析命令行选项的函数，它是C语言中标准库 <unistd.h> 中提供的函数。

getopt 函数可以帮助程序解析命令行参数，并提供了一种方便的方式来处理选项和选项参数。它支持简化的单字符选项（短选项）以及长选项（长选项）的解析。

以下是 getopt 函数的常见参数和用法：

int getopt(int argc, char *const argv[], const char *optstring);

argc：命令行参数的数量，即 main 函数的参数 argc。

argv：命令行参数的数组，即 main 函数的参数 argv。

optstring：指定程序支持的选项字符串。

getopt 函数会迭代解析命令行参数，并返回下一个选项的字符。当解析完所有的选项后，getopt 函数返回 -1，表示解析完毕。

在循环中调用 getopt 函数，可以逐个获取命令行参数中的选项和选项参数。例如：

#include <stdio.h>
#include <unistd.h>int main(int argc, char *argv[]) {int opt;while ((opt = getopt(argc, argv, "abc:")) != -1) {switch (opt) {case 'a':printf("Option -a is set\n");break;case 'b':printf("Option -b is set\n");break;case 'c':printf("Option -c is set, value: %s\n", optarg);break;case '?':fprintf(stderr, "Unknown option: %c\n", optopt);return 1;default:break;}}for (int i = optind; i < argc; i++) {//非选项参数printf("Non-option argument: %s\n", argv[i]);}return 0;
}

以上示例代码解析了以下几种命令行参数：

单字符选项：

-a：表示选项 -a 被设置。

-b：表示选项 -b 被设置。
带参数的选项：

-c value：表示选项 -c 被设置，并且其参数为 value。
非选项参数（操作数）：

通过循环使用 getopt 函数，可以依次获取每个选项及其参数，并使用 switch 语句进行处理。同时，可以在 optind 后的循环中获取非选项参数（操作数），并进行相应的处理。

需要注意的是，选项字符串中的冒号（:）可以用来指示带有参数的选项。例如，"abc:" 表示选项 -c 将带有参数。在 switch 语句中，optarg 变量用于获取选项的参数。

总结：
getopt 函数是一个用于解析命令行选项的函数。它通过遍历命令行参数，逐个解析选项和选项参数，并提供了一种方便的方式来处理命令行选项。通过了解 getopt 函数的使用方法，可以编写灵活的命令行工具，支持选项的解析和处理。

四、optstring规则的扩展定义

1.+ ：将 getopt 函数的错误消息输出到 stderr（标准错误流）而不是 stdout（标准输出流）。通常情况下，错误消息会被发送到 stdout。使用 + 标志可以将错误消息重定向到 stderr，这样可以将标准输出用于其他目的。

2.- ：使 getopt 函数返回一个非选项参数（即不以 - 或 – 开头的参数），作为额外的非选项参数。通常情况下，getopt 函数只返回选项字符，而将其他所有参数视为非选项参数。使用 - 标志可以将非选项参数作为额外的返回结果。

3.: ：表示该选项需要一个参数。如果一个选项需要一个参数，但未提供该参数，则 getopt 函数将返回特殊值 ‘:’，并在 optopt 中存储选项字符。

#include <stdio.h>
#include <unistd.h>int main(int argc, char** argv)
{int opt = -1;while((opt = getopt(argc, argv, ":abc:")) != -1){switch (opt){case 'a':printf("Option -a is set\n");break;case 'b':printf("Option -b is set\n");break;case 'c':printf("Option -c is set, value: %s\n", optarg);break;case '?':printf("Unknow option: -%c\n", optopt);break;        default:break;}}for(int i = optind; i < argc; i++){printf("Non-option argument: %s\n", argv[i]);}return 0;
}

修改代码加上+符号，取消输出错误信息：
运行结果：

总结

本篇文章就讲解到这里。