朴素贝叶斯法的学习与分类

《统计学习方法》李航第四章

1、概述

书上对朴素贝叶斯的描述如下：

朴素贝叶斯法时基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。

其实目的就是要得到最大的$P(Y|X)$。根据先验概率$P(X)$和求出的输出Y和输入特征X之间的联合概率分布$P(X,Y)$，进而计算出$P(Y|X)=\frac{P(X,Y)}{P(X)}$.是生成模型。

2、先验概率、后验概率和条件概率

书中描述提到了后验概率，要先弄清楚什么是后验概率。
先验概率：指根据以往的经验和分析，在实验或采样前就可以得到的概率。
后验概率：指某件事已经发生，计算这件事发生的原因时由某个因素引起的概率。

书中关于朴素贝叶斯的数学描述如下：

这里提到了条件概率，
条件概率：在给定事件B发生的条件下，事件A发生的概率，记为$P(A|B)$，有$P(A|B)=\frac{P(AB)}{P(B)}$。
查看书中给出的条件概率的计算公式，发现可以按照刚刚的后验概率来理解，即$P(X=x|Y=c_k)$其实求的就是：$Y=c_k$这件事已经发生，计算这件事发生是由$X=x$引起的概率，记为$P(X=x|Y=c_k)$.但是书中为什么说是条件概率而不是后验概率呢？
查询可知，其实后验概率就是一种条件概率，但是与其它条件概率的不同之处在于，它限定了目标事件为隐变量取值，而其中的条件为观测结果。一般的条件概率，条件和事件都可以是任意的。也就是说，后验概率其实是限制了关注点的条件概率，重点关注目标事件，是一个执果索因的过程。

3、条件独立性假设

朴素贝叶斯法对条件概率分布作了条件独立性假设，由于这是一个较强的假设，朴素贝叶斯法也由此得名，具体的，条件独立性假设是：
$$\begin{gathered} P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k) \\ =\prod _{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k) \end{gathered}$$
条件独立假设等于是说用于分类的特征在类确定的条件下都是条件独立的。属于生成模型。

4、朴素贝叶斯分类器

朴素贝叶斯分类时，对给定的输入x，通过学习得到的模型计算后验概率分布$P(Y=c_k|X=x)$，将后验概率最大的类作为x的类输出。即：
$$\begin{gathered} P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{{\sum }_{k}P(X=x|Y=c_k)P(Y=c_k)} \\ =\frac{P(Y=c_k){\prod }_{j}P(X^{(j)}=x^{(j)}|Y=c_k)}{{\sum }_{k}P(Y=c_k){\prod }_{j}P(X^{(j)}=x^{(j)}|Y=c_k)} \end{gathered}$$

因为求最大且对于所有$c_k$分母都是相同的，
所以：
$$y=arg\underset{c_k}{\max }P(Y=c_k)\prod _{j}P(X^{(j)}=x^{(j)}|Y=c_k)$$

5、算法流程

利用朴素贝叶斯分类器分类的大致流程可以理解为以下过程：
已知
假设分类的模型样本是$$(x_1^{(1)},x_2^{(1)},...,x_n^{(1)},y_1),(x_1^{(2)},x_2^{(2)},...,x_n^{(2)},y_2),...(x_1^{(m)},x_2^{(m)},...,x_n^{(m)},y_m)$$
即我们有m个样本，每个样本有n个特征，输出特征有K个类别，定义为$C_1,C_2,...,C_k$.

中间推导

• 根据朴素贝叶斯模型的基本原理，要得出最大的$P(Y=c_k|X=x)$，就需要计算先验概率$P(Y=c_k)$和联合概率分布$P(X,Y=c_k)$.

• 而从样本通过极大似然估计很容易得知先验概率$P(Y=c_k)$和条件概率分布 $P(X=x|Y=c_k)=P(X_1=x1，X_2=x_2,...,X_n=x_n|Y=c_k)$：
  先验概率$P(Y=c_k)$的极大似然估计是：
  $$P(Y=c_k)=\frac{{\sum }_{i=1}^{N}I(y_i=c_k)}{N}$$(其实就是$Y=c_k$在训练集分类中出现的占比)
  设第$j$个特征$x^{(j)}$可能取值的集合为$a_{j1},a_{j2},...,a_{j{S}_j}$，条件概率$P(X^{(j)}=a_{jl}|Y=c_k)$的极大似然估计是$$P(X^{(j)}=a_{jl}|Y=c_k)=\frac{{\sum }_{i=1}^{N}I(x_i^{(j)}=a_{jl},y_i=c_k)}{{\sum }_{i=1}^{N}I(y_i=c_k)}$$

• 因此可以求得联合概率分布$$\begin{gathered} P(X,Y=c_k)=P(Y=c_k)P(X=x|Y=c_k) \\ =P(Y=c_k)P(X_1=x_1,X_2=x_2,...,X_n=x_n|Y=c_k) \\ =P(Y=c_k){\prod }_{j=1}^{n}P(X_j=x_j|Y=c_k) \end{gathered}$$.

结果
求出$$y=arg\underset{c_k}{\max }P(Y=c_k|X=x)=arg\underset{c_k}{\max }\frac{P(X,Y=c_k)}{P(X)}$$
即$$y=arg\underset{c_k}{\max }P(Y=c_k)\prod _{j=1}^{n}P(X_j=x_j|Y=c_k)$$结果最大的$k$即为输入$X$对应的类别$C_k$.

训练实例：

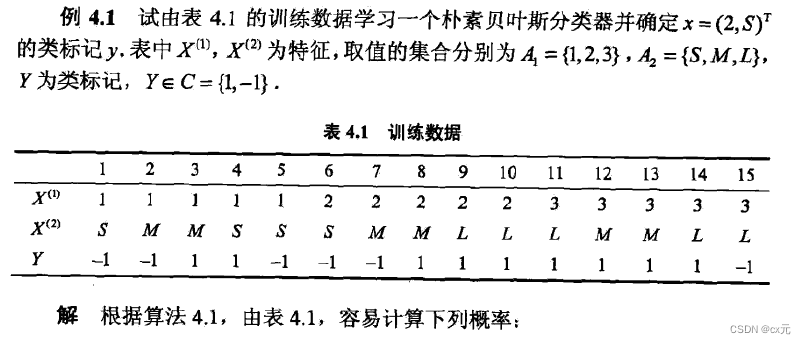
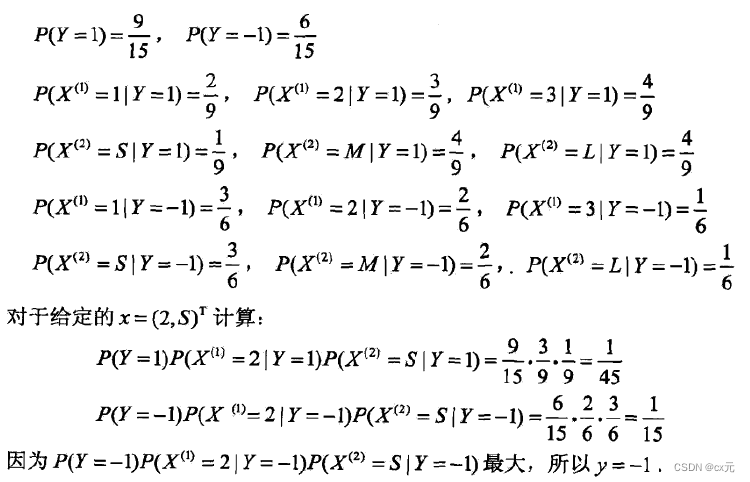
6、贝叶斯和朴素贝叶斯

因为朴素贝叶斯的概率估计方法采用的是极大似然估计，极大似然估计可能会造成估计结果为0的情况，导致无法进行后续计算，所以引入贝叶斯估计方法。

7、注意

朴素贝叶斯使用的前提就是条件独立假设，即假设输入变量都是条件独立互不影响的，如果条件之间存在依存关系，则模型就变成了贝叶斯网络。