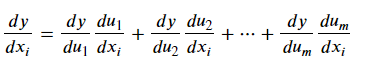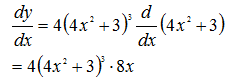来看复合函数如何求导：

现实中要解决的问题，大多可以总结为这三种函数的组合

减法可以看做是加上某个函数的-1倍

除法可以转化为乘法

先来看加法

两个函数的和的导数，就是他们导数的和

两个函数sin（x）和$x^2$

它们的和就是黄色这条线代表的函数

在x=0.5是他们的和这样表示

在数学上表示为x=0.5加上微小变化量dx处，sin（0.5+dx）的和$(0.5+dx{)}^2$的值相加后的导数

上式中sin(x)的导数是cos(x),$x^2$的导数是$2x^1$也就是2x

可得：$\frac{df}{dx}=cos(x)+2x$

乘法：

来看$f(x)=sin(x)x^2$ 的导数

乘法表示的函数，我们一般用面积大方法表示更直观：

对比上图，调整x的取值，会引起两个函数的变化，从而影响面积的变化

（$sin(x)$ 的变化域在[-1,1]之间）

它的微小变化量我们任然用增加面积来表示：

宽度增加的值是$d(sin(x))$
高度增加了$d(x^2)$
(注意这里的变化是想的变化引起的函数结果的变化)

这样第一个长条的面积就是 ：长$sin(x)$ × 高(增加的微小变化量)$d(x^2)$

加上第二个竖长条的面积，

第三个小块可以忽略不计

当dx趋近于0的时候，他的面积可以看做是正方形的面积$d(x^2)$,所以忽略不计，

意味着$d(sin(x))$和$d(x^2)$同样非常非常小

(2x代表x取一小段变化起点出处的导数，2x乘以dx才代表这一小段微小变化量的导数)

我们知道了导数$d(sin(x))$和$d(x^2)$的值，带入：

口诀：左乘右导，右乘左导

左边的函数 乘以右边函数的导数，加上右边的函数 乘以左边函数的导数

例如求一个常数乘以函数的导数

用面积表示为：

增加的小块面积=宽$d(sin(x))$ ×高_常数

加入常数为2，则 2×$d(sin(x))$ =2cos(x)

再来看另外一种符合函数

这次我们用三个数轴表示函数

x变化是时，第二，三数轴引起的变化

把中间的$x^2$看做h
则h增加了dh
$sin(h)$增加了$d(sin(h))$

$d(sin(h))$展开就是$cos(h)\ast dh$

给x赋值1.5
带入得到：

一直$d(x^2)$=2xdx

再次展开

带入1.5

上式理解：

$sin(x^2)$ 的导数是 $cos(x^2)$，它的系数是$d(x^2)$,也就是$x^2$的导数，而$x^2$的导数是2x，它的系数是dx，从右向左理解

由此，对于复合函数