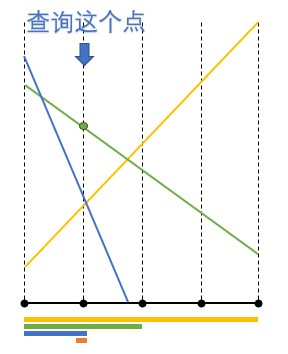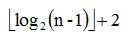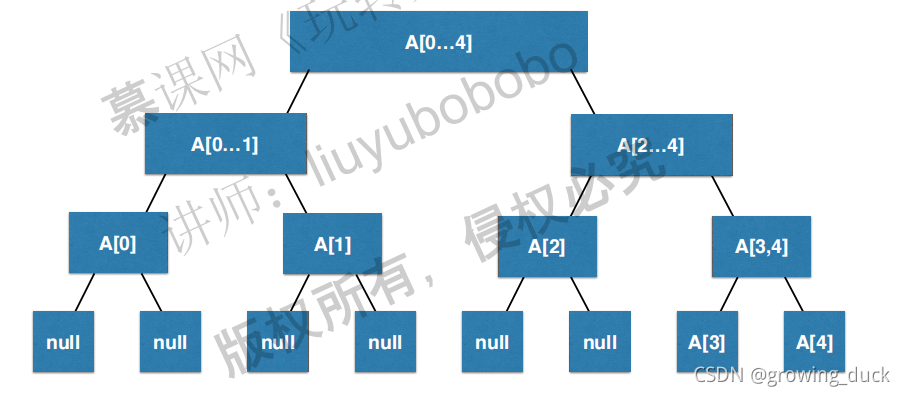
如上图：

线段树是一颗满二叉树，叶子节点如果没有值，用null表示。 非空叶子节点就是基础数据，树中每个父亲节点代表左右孩子的结果集（比如求合，最大值，最小值等，自己定义算法，传入左右孩子即可）。

那么有n个元素，构建线段树需要开辟多少空间？

对于满二叉树，每一层节点数量都是前面所有节点数量之和+1。 也就是说，如果最后一层有n个节点，整棵树就约为2n个节点。

如果此时n为2的k次方，所有元素刚好在最后一层，整棵树约就是2n。   如果再多一个元素，就需要开辟下一层空间，如上图那样，整棵树就需要开辟4n的空间。

构建线段树：

使用两个数组来构建线段树，一个数组表示原始数据，另一个数组表示线段树。

如上图所示，如果传入一个数组，如何把它构建为线段树？ 

public class SegmentTree<E> {//存储数据private E[] data;//用数组表示树结构private E[] tree;//定义算法类，计算左右孩子的结果。 此例中为求合private Merger<E> merger;//外界传入一个数组arr，将它构建为线段树（每个树节点就是左右孩子的和）public SegmentTree(E[] arr, Merger<E> merger) {this.merger = merger;data = (E[]) new Object[arr.length];for (int i = 0; i < arr.length; i++) {data[i] = arr[i];}tree = (E[]) new Object[4 * arr.length];buildSegmentTree(0, 0, arr.length - 1);}// 在treeIndex的位置创建表示区间[l...r]的线段树private void buildSegmentTree(int treeIndex, int l, int r) {if (l == r) {tree[l] = data[l];return;}int leftTreeIndex = leftChild(treeIndex);int rightTreeIndex = rightChild(treeIndex);int mid = (l + r) / 2;
//        int mid = l + (r - l) / 2;buildSegmentTree(leftTreeIndex, l, mid);buildSegmentTree(rightTreeIndex, mid + 1, r);tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);}// 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引private int leftChild(int index) {return 2 * index + 1;}// 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引private int rightChild(int index) {return 2 * index + 2;}public int getSize() {return data.length;}public E get(int index) {if (index < 0 || index >= data.length) {throw new IllegalArgumentException("Index is illegal.");}return data[index];}// 返回区间[queryL, queryR]的值public E query(int queryL, int queryR) {if (queryL < 0 || queryL >= data.length ||queryR < 0 || queryR >= data.length || queryL > queryR) {throw new IllegalArgumentException("Index is illegal.");}return query(0, 0, data.length - 1, queryL, queryR);}// 在以treeIndex为根的线段树中[l...r]的范围里，搜索区间[queryL...queryR]的值private E query(int treeIndex, int l, int r, int queryL, int queryR) {if (l == queryL && r == queryR) {return tree[treeIndex];}int leftTreeIndex = leftChild(treeIndex);int rightTreeIndex = rightChild(treeIndex);int mid = (l + r) / 2;if (queryL >= mid + 1) {return query(rightTreeIndex, mid + 1, r, queryL, queryR);} else if (queryR <= mid) {return query(leftTreeIndex, l, mid, queryL, queryR);}E leftResult = query(leftTreeIndex, l, mid, queryL, mid);E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);return merger.merge(leftResult, rightResult);}// 将index位置的值，更新为epublic void set(int index, E e) {if (index < 0 || index >= data.length) {throw new IllegalArgumentException("Index is illegal");}//直接把数据数组中对应的值改掉data[index] = e;//重构线段树set(0, 0, data.length - 1, index, e);}// 在以treeIndex为根的线段树中更新index的值为eprivate void set(int treeIndex, int l, int r, int index, E e) {//说明找到树中最底层那个节点了if (l == r) {tree[treeIndex] = e;return;}int mid = (l + r) / 2;int leftTreeIndex = leftChild(treeIndex);int rightTreeIndex = rightChild(treeIndex);if (index > mid) {set(rightTreeIndex, mid + 1, r, index, e);} else {set(leftTreeIndex, l, mid, index, e);}tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);}
}

public interface Merger<E> {/*** 计算两个节点的结果集* @param a* @param b* @return*/E merge(E a, E b);
}

做一道题：

/*** 给你一个数组 nums ，请你完成两类查询，其中一类查询要求更新数组下标对应的值，另一类查询要求返回数组中某个范围内元素的总和。* <p>* 实现 NumArray 类：* <p>* NumArray(int[] nums) 用整数数组 nums 初始化对象 void update(int index, int val) 将 nums[index] 的值更新为 val int sumRange(int left,* int right) 返回子数组 nums[left, right] 的总和（即，nums[left] + nums[left + 1], ..., nums[right]）* <p>* 来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/range-sum-query-mutable 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。*/
public class NumArray {private SegmentTree<Integer> tree;public NumArray(int[] nums) {if (nums.length != 0) {Integer[] data = new Integer[nums.length];for (int i = 0; i < nums.length; i++) {data[i] = nums[i];}tree = new SegmentTree<Integer>(data, (a, b) -> a + b);}}public void update(int i, int val) {tree.set(i,val);}public int sumRange(int i, int j) {return tree.query(i,j);}
}