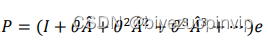Random Walk Approaches for Node Embeddings
一、随机游走基本概念

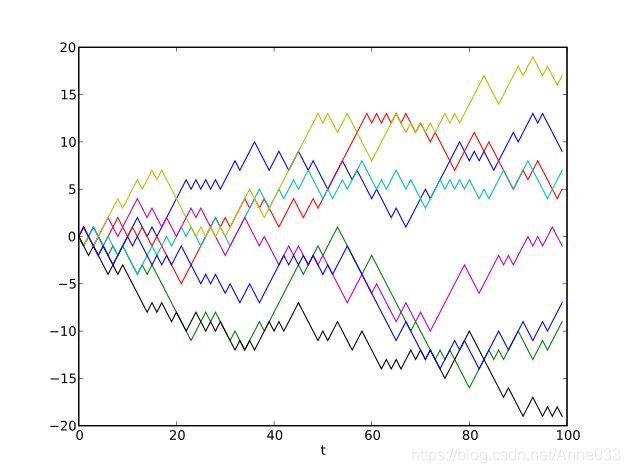
想象一个醉汉在图中随机的行走,其中走过的节点路径就是一个随机游走序列。
随机行走可以采取不同的策略,如行走的方向、每次行走的长度等。
二、图机器学习与NLP的关系

从图与NLP的类比关系可以看出,图机器学习和NLP相似度很高,了解两者的类比关系可以加深对图机器学习的理解。
随机游走的根本目标是对图中的各个节点进行编码,将图中的各个节点编码成可供下游任务使用的向量,即编码器。因此,随机游走是一个无监督/自监督算法,没有使用任何标签。
三、概念定义(可以先看后面,用到时再看概念)

-
z u \mathbf{z} _u zu:期望获得的节点 u u u的嵌入向量,是算法的目标
-
P ( v ∣ z u ) P(v|\mathbf{z} _u) P(v∣zu):从 u u u节点出发的随机游走序列经过 v v v节点的概率。
如果 u u u节点和 v v v节点出现在同一个随机游走序列,那么 P P P值应该高;如果 u u u节点和 v v v节点没有出现在同一个随机游走序列,那么期望 P P P应该低,这也是之后优化算法的根本思路。
-
P ( v ∣ z u ) P(v|\mathbf{z} _u) P(v∣zu)的计算:本文使用softmax计算 P P P值,具体计算方法在“五、优化算法”中,这里只介绍两个非线性函数
-
softmax:将k维的向量的值通过softmax改为k维的概率值,其中:
σ ( z ) [ i ] = e z [ i ] ∑ j = 1 K e z [ j ] \sigma(z)[i]=\frac{e^{z[i]}}{\sum_{j=1}^K e^{z[j]}} σ(z)[i]=∑j=1Kez[j]ez[i] -
sigmoid:将k维嵌入向量的值映射到0-1,其中:
S ( x ) = 1 1 + e − x S(x)=\frac{1}{1 + e^{-x}} S(x)=1+e−x1
-
-
相似度similarity:数量积(余弦相似度)
因为嵌入向量 z z z在最后都通过计算使其度量(向量长度)相同,所以可以直接求向量积来代表其相似度。
s i m i l a r i t y = z u T z v similarity=\mathbf{z} _u ^T \mathbf{z} _v similarity=zuTzv -
N R ( u ) N_R(u) NR(u):选定游走策略为R,在 u u u节点为起点的条件下,访问得到的节点的集合。
四、随机游走算法
1、特征学习优化策略:

优化算法总目标:对于给定的图 G G G,随机游走的目标是找到一个函数 f f f,其可以将节点 u u u映射为 d d d维的向量 z u \mathbf{z} _u zu。
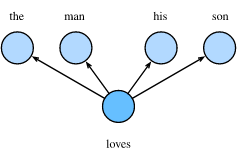
似然目标函数:如图,在确定出发节点 u u u的条件下(即向量 z u \mathbf{z} _u zu),与 u u u节点同一序列的节点集合 N R ( u ) N_R(u) NR(u)中的节点出现的概率最大。可以看出其本质是极大似然估计。
2、随机游走优化策略:

- 选定游走策略R,对每个节点 u u u进行固定长度的随机游走。
- 对每个节点 u u u,收集 N R ( u ) N_R(u) NR(u)。
- 对于给定的节点 u u u与 N R ( u ) N_R(u) NR(u),更新 z u \mathbf{z} _u zu,使优化目标函数最大。最终得到的 z u \mathbf{z} _u zu即维节点 u u u的嵌入向量。
其中,优化目标函数在随机游走算法中等同于:

其中,第一个求和符号 u ∈ V u \in V u∈V代表遍历图 G G G的所有节点,第二个求和符号 v ∈ N R ( u ) v \in N_R(u) v∈NR(u)代表遍历所有 N R ( u ) N_R(u) NR(u)中的节点, l o g log log加负号使求最大变为求最小,这样,优化目标函数变为了损失函数。
P ( v ∣ z u ) P(v|\mathbf{z} _u) P(v∣zu)使用softmax进行求解。
进一步解释如图:

3、随机游走算法的优化—负样本:

从图中可以看出,在计算softmax时,需要遍历图 G G G的顶点两次,时间复杂度为 O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2),这是不可接受的。
在此使用负采样解决softmax难算问题:

如图,在计算softmax时,对于分母,不用计算图中所有的节点,而是采样 k k k个负节点进行计算。注意:图 G G G中每个节点的采样概率是不同的,在Node2Vec中采用类似于Word2Vec中词频的方法。
此方法原理解释如下:

关于K的取值是一个超参数:

更高的K意味着采样更多的点,这回增加模型的健壮性。但是相同的更多的会引入更多的负样本,这回导致正负样本失衡,影响训练,因此一般来说K的取值在5到20之间。理论上,同一个随机游走序列中的节点不应被采样为负样本。
4、优化过程—随机梯度下降
因这里是机器学习的基础,故在此不做赘述:


五、总结

- 选定游走策略R,对每个节点 u u u进行固定长度的随机游走。
- 对每个节点 u u u,收集 N R ( u ) N_R(u) NR(u)。
- 利用损失函数,采用随机梯度方法对 z u \mathbf{z} _u zu进行优化。损失函数可以采用负样本算法简化计算。
本文只是将游走策略抽象为R,那么具体什么样的策略是真正有效的呢,DeepWalk和Node2Vec提供了可以参考的具体思路。
图片截选自——斯坦福CS224W: Machine Learning with Graphs