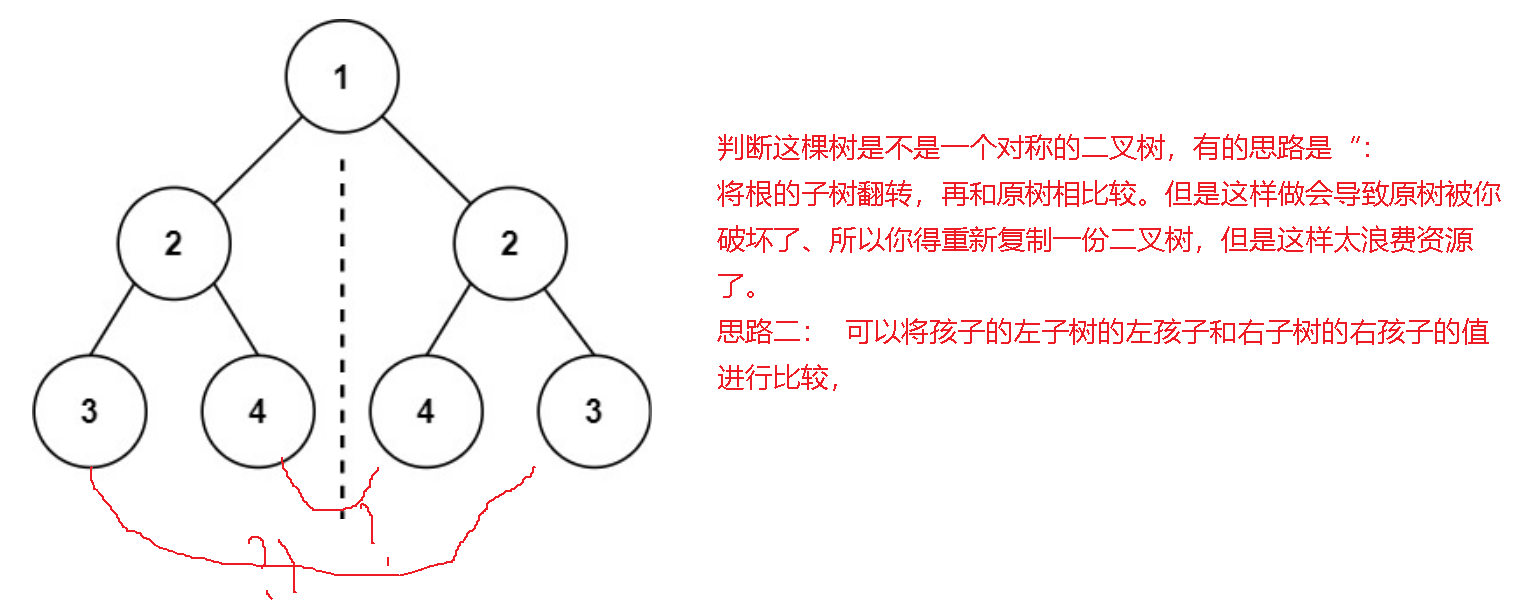
前言

承接上节，树的非递归三种遍历我们使用了栈，今天讲解的树的层序遍历，我们需要使用另外一种数据结构——队列
我们先简单的回忆一下什么是队列

1.队列

概念：一端入元素，另一端出元素的线性表
一端：队尾
另一端：队头
线性表：顺序表，链表

接下来我们就来完成树的层序遍历吧！

1.根结点入队
2.打印根结点的值并判断当前结点是否有左右子结点
若有，则左右依次入队，此时出队一个元素，并访问其左右子结点
若无，则遍历结束

void LevelOrder(TreeNode* T) {//二叉树的层序遍历if (T == NULL)return;TreeNode* Queue[MaxSize];//队列int front, rear;front = rear = 0;//队空TreeNode* p = NULL;//遍历指针//1.让根节点入队rear = (rear + 1) % MaxSize;Queue[rear] = T;while (front != rear) {front = (front + 1) % MaxSize;p = Queue[front];printf("%d ", p->data);if (p->left != NULL) {//判读左孩子rear = (rear + 1) % MaxSize;Queue[rear] = p->left;}if (p->right != NULL) {//判断右孩子rear = (rear + 1) % MaxSize;Queue[rear] = p->right;}}}

完整代码如下

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#define MaxSize 20typedef struct TreeNode {int data;struct TreeNode* left;struct TreeNode* right;
}TreeNode;void LevelOrder(TreeNode* T) {//二叉树的层序遍历if (T == NULL)return;TreeNode* Queue[MaxSize];//队列int front, rear;front = rear = 0;//队空TreeNode* p = NULL;//遍历指针//1.让根节点入队rear = (rear + 1) % MaxSize;Queue[rear] = T;while (front != rear) {front = (front + 1) % MaxSize;p = Queue[front];printf("%d ", p->data);if (p->left != NULL) {//判读左孩子rear = (rear + 1) % MaxSize;Queue[rear] = p->left;}if (p->right != NULL) {//判断右孩子rear = (rear + 1) % MaxSize;Queue[rear] = p->right;}}}int main() {TreeNode n1;TreeNode n2;TreeNode n3;TreeNode n4;n1.data = 1;n2.data = 3;n3.data = 5;n4.data = 7;n1.left = &n2;n1.right = &n3;n2.left = &n4;n2.right = NULL;n3.left = NULL;n3.right = NULL;n4.left = NULL;n4.right = NULL;printf("层序遍历为：");LevelOrder(&n1);return 0;
}