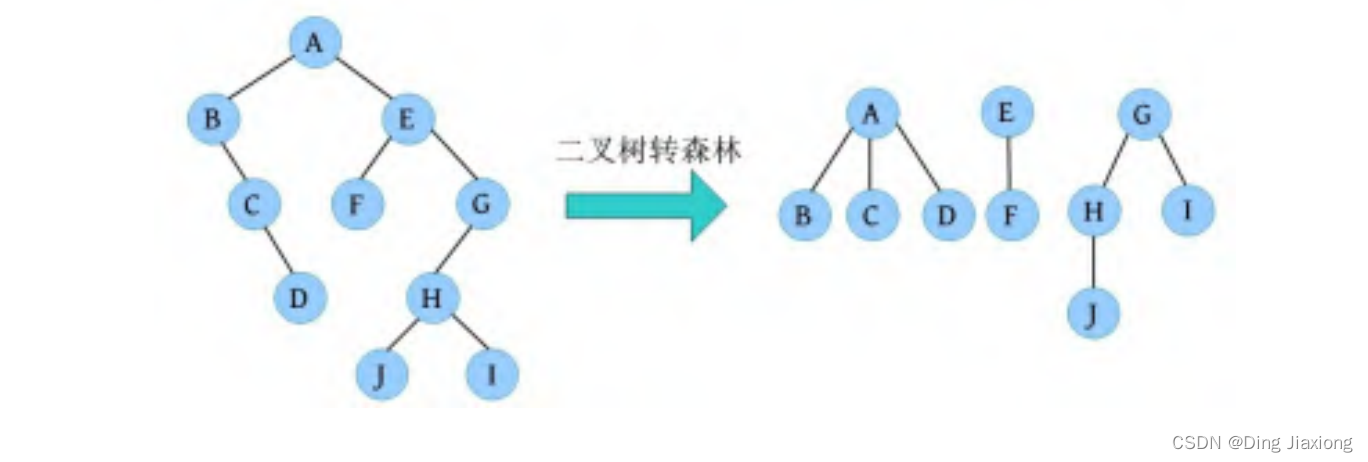
二叉树的层序遍历

article/2025/9/18 19:41:53

二叉树的层序遍历

  • 1.层序遍历
  • 2.实例
    • 2.1二叉树的层序遍历
    • 2.2 二叉树的层序遍历 II
    • 2.3 二叉树的右视图
    • 2.4 二叉树的层平均值
    • 2.5 N叉树的层序遍历
    • 2.6在每个树行中找最大值
    • 2.7二叉树的最大深度
    • 2.8二叉树的最小深度
    • 2.9翻转二叉树
    • 2.10完全二叉树的节点个数
    • 2.11左叶子之和
    • 2.11找树左下角的值

1.层序遍历

层序遍历一个二叉树。就是从左到右一层一层的区遍历二叉树。为了实现层序遍历，我们需要借助一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

2.实例

2.1二叉树的层序遍历

在这里插入图片描述

二叉树的层序遍历

思路：
1.创建队列用来存储节点，创建list集合用来存储结果
2.逐层记录结果即可。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> ans = new ArrayList<>();//用来输出结果Queue<TreeNode> queue  = new LinkedList<>();//创建一个队列，用来逐层存放if(root==null) return ans;queue.offer(root);while(!queue.isEmpty()){List<Integer> list = new ArrayList<>();//用于存放值int len = queue.size();for(int i=0;i<len;i++){TreeNode temp = queue.poll();list.add(temp.val);//放进listif(temp.left!=null) queue.offer(temp.left);if(temp.right!=null) queue.offer(temp.right);}ans.add(list);}return ans;}
}

2.2 二叉树的层序遍历 II

在这里插入图片描述
二叉树的层序遍历 II

思路：
和上题基本一致，只需要在输出结果之前将结果反转即可。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<List<Integer>> levelOrderBottom(TreeNode root) {List<List<Integer>> ans = new ArrayList<>();//用来输出结果Queue<TreeNode> queue  = new LinkedList<>();//创建一个队列，用来逐层存放if(root==null) return ans;queue.offer(root);while(!queue.isEmpty()){List<Integer> list = new ArrayList<>();//用于存放值int len = queue.size();for(int i=0;i<len;i++){TreeNode temp = queue.poll();list.add(temp.val);//放进listif(temp.left!=null) queue.offer(temp.left);if(temp.right!=null) queue.offer(temp.right);}ans.add(list);}//将ans反转即可List<List<Integer>> ans1 = new ArrayList<>();for(int i=ans.size()-1;i>=0;i--){ans1.add(ans.get(i));}return ans1;}
}

2.3 二叉树的右视图

在这里插入图片描述
二叉树的右视图

和模板思路一致，只不过添加的是队列的最后一个元素
if(i==len-1){//保证当前的最后后子节点
ans.add(temp.val);
}

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Integer> rightSideView(TreeNode root) {List<Integer> ans = new ArrayList<>();//用来输出结果Queue<TreeNode> queue = new LinkedList<>();//队列用来存放节点if(root==null) return ans;queue.offer(root);while(!queue.isEmpty()){int len = queue.size();for(int i=0;i<len;i++){TreeNode temp = queue.poll();if(i==len-1){//保证当前的最后后子节点ans.add(temp.val);}if(temp.left!=null) queue.offer(temp.left);if(temp.right!=null) queue.offer(temp.right);}}return ans;}
}

2.4 二叉树的层平均值

在这里插入图片描述
二叉树的层平均值

依旧套用模板，只是在记录每一层的值，并输出即可。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Double> averageOfLevels(TreeNode root) {List<Double> ans =new ArrayList<>();//用于输出答案Queue<TreeNode> queue = new LinkedList<>();//用于存放节点if(root==null) return ans;queue.offer(root);//将节点存入队列中while(!queue.isEmpty()){int len = queue.size();Double sum = 0.0;for(int i = 0;i<len;i++){TreeNode temp = queue.poll();sum+=temp.val;if(temp.left!=null) queue.offer(temp.left);if(temp.right!=null) queue.offer(temp.right);}ans.add(sum/len);}return ans;}
}

2.5 N叉树的层序遍历

在这里插入图片描述
N叉树的层序遍历

本题我们需要注意的是如何添加孩子节点。

/*
// Definition for a Node.
class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List<Node> _children) {val = _val;children = _children;}
};
*/class Solution {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> ans = new ArrayList<>();//用于输出答案Queue<Node>  queue = new LinkedList<>();//用于存储节点if(root==null) return ans;queue.offer(root);//将节点存入队列中while(!queue.isEmpty()){int len = queue.size();List<Integer> list = new ArrayList<>();//记录每层的值for(int i=0;i<len;i++){Node temp = queue.poll();list.add(temp.val);List<Node> children = temp.children;//记录temp的孩子节点if(children==null||children.size()==0) continue;for(Node child:children){if(child!=null){//如果孩子节点不为空queue.offer(child);//添加到队列}}}ans.add(list);}return ans;}
}

2.6在每个树行中找最大值

在这里插入图片描述
在每个树行中找最大值

注意注意Collection.max()这一方法，输出集合中的最大值

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Integer> largestValues(TreeNode root) {List<Integer> ans = new ArrayList<>();//用于输出答案Queue<TreeNode> queue = new LinkedList<>();//用于存放节点if(root==null) return ans;queue.offer(root);//存放当前节点while(!queue.isEmpty()){int len = queue.size();List<Integer> list = new ArrayList<>();//用于记录每一层的值for(int i=0;i<len;i++){TreeNode temp = queue.poll();//暂时存放节点list.add(temp.val);//记录没层的所有值if(temp.left!=null) queue.offer(temp.left);if(temp.right!=null) queue.offer(temp.right);}ans.add(Collections.max(list));//注意Collection.max()}return ans;}
}

2.7二叉树的最大深度

在这里插入图片描述

二叉树的最大深度

遍历完每一层时深度加一即可。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int maxDepth(TreeNode root) {Queue<TreeNode> queue = new LinkedList<>();//存放节点int depth=0;if(root==null) return depth;queue.offer(root);//将节点入队while(!queue.isEmpty()){int len = queue.size();for(int i=0;i<len;i++){TreeNode temp = queue.poll();if(temp.left!=null) queue.offer(temp.left);if(temp.right!=null) queue.offer(temp.right);}depth++;//层数加一}return depth;}
}

2.8二叉树的最小深度

在这里插入图片描述
二叉树的最小深度

只需要找出左右节点都为null的节点，返回当前深度即可。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int minDepth(TreeNode root) {List<Integer> ans = new ArrayList<>();Queue<TreeNode> queue = new LinkedList<>();if(root==null) return 0;queue.offer(root);//根节点入队int depth=0; while(!queue.isEmpty()){depth++;//每进入一层，depth++int len = queue.size();for(int i=0;i<len;i++){TreeNode temp = queue.poll();//找到叶子节点if(temp.left==null&&temp.right==null) return depth;if(temp.left!=null) queue.offer(temp.left);if(temp.right!=null) queue.offer(temp.right);}}return depth;}
}

2.9翻转二叉树

在这里插入图片描述
反转二叉树

思路：使用层序遍历，然后将该层的左右子树翻转即可。


```java
/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {/** 层序遍历*/public TreeNode invertTree(TreeNode root) {Queue<TreeNode> queue =new LinkedList<>();if(root==null) return null;queue.offer(root);//根节点入队while(!queue.isEmpty()){int len = queue.size();for(int i=0;i<len;i++){TreeNode temp=queue.poll();//取出当前根节点swapChild(temp);//交换根节点的左右子节点//继续收集下一层的节点if(temp.left!=null) queue.offer(temp.left);if(temp.right!=null) queue.offer(temp.right);}}return root;}//交换根节点的左右子节点private void swapChild(TreeNode root){TreeNode temp = root.left;root.left=root.right;root.right=temp;}
}

2.10完全二叉树的节点个数

在这里插入图片描述

完全二叉树的节点个数

依旧使用层序遍历，定义一个计数器记录节点个数即可

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int countNodes(TreeNode root) {if(root==null) return 0;Queue<TreeNode> queue = new LinkedList<>();//存储节点int num =0;//记录节点个数queue.offer(root);while(!queue.isEmpty()){int len = queue.size();for(int i=0;i<len;i++){TreeNode temp = queue.poll();//出队num++;if(temp.left!=null) queue.offer(temp.left);if(temp.right!=null) queue.offer(temp.right);}}return num;}
}

2.11左叶子之和

在这里插入图片描述

左叶子之和

本题依旧可以使用层序遍历，解题的关键是如何找到左叶子节点的

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int sumOfLeftLeaves(TreeNode root) {if(root==null) return 0;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int sum=0;while(!queue.isEmpty()){TreeNode temp=queue.poll();//注意左叶子的判断if(temp.left!=null&&temp.left.left==null&&temp.left.right==null){sum+=temp.left.val;}if(temp.left!=null) queue.offer(temp.left);if(temp.right!=null) queue.offer(temp.right);}return sum;}
}

2.11找树左下角的值

在这里插入图片描述
找树左下角的值

注意int的使用，只有一个值

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/class Solution {/**注意只有一个值，所有用int*/public int findBottomLeftValue(TreeNode root) {int ans=0;Queue<TreeNode> queue =new LinkedList<>();//放节点queue.offer(root);while(!queue.isEmpty()){int len =queue.size();for(int i=0;i<len;i++){TreeNode temp = queue.poll();//取出当前节点if(i==0) ans = temp.val;if(temp.left!=null) queue.offer(temp.left);if(temp.right!=null)  queue.offer(temp.right);}}return ans;}
}

http://chatgpt.dhexx.cn/article/KP6Wrmjg.shtml

相关文章

二叉树的遍历——层序遍历

二叉树的遍历——层序遍历

一、之前写了二叉树的三种遍历方法&#xff1a;有先序遍历、中序遍历、后序遍历&#xff0c;这三种方法都是用递归的方式来遍历二叉树的。层序遍历则不是使用递归来遍历&#xff0c;而是使用队列的来实现遍历&#xff1a; void LevelTreeOrder(BTNode* root) {Queue q;QueueIni…
阅读更多...
LDA算法简单推导

LDA算法简单推导

阅读更多...
【机器学习】LDA算法 (主题模型算法)

【机器学习】LDA算法 (主题模型算法)

随着互联网的发展&#xff0c;文本分析越来越受到重视。由于文本格式的复杂性&#xff0c;人们往往很难直接利用文本进行分析。因此一些将文本数值化的方法就出现了。LDA就是其中一种很NB的方法。 LDA有着很完美的理论支撑&#xff0c;而且有着维度小等一系列优点。本文对LDA算…
阅读更多...
LDA算法和PCA算法的总结(原理和思想)

LDA算法和PCA算法的总结(原理和思想)

LDA和PCA的对比(并没有公式推导&#xff0c;改日会写) 先补一补数学(不需要)&#xff1a; 方差——概率论和统计方差衡量随机变量或一组数据时离散程度的度量&#xff1b;概率论中方差用来度量随机变量和其数学期望之间的偏离程度。统计中的方差&#xff08;样本方差&#xff…
阅读更多...
LDA算法原理及LDA与PCA的比较

LDA算法原理及LDA与PCA的比较

1. LDA算法简介 LDA&#xff08;线性判别式分析 Linear Discriminant Analysis&#xff09;属于机器学习中的监督学习算法&#xff0c;常用来做特征提取、数据降维和任务分类。在人脸识别、人脸检测等领域发挥重要作用。LDA算法与PCA算法都是常用的降维技术。二者的区别在于&a…
阅读更多...
LDA算法调研报告

LDA算法调研报告

LDA算法调研报告 1、LDA算法概述 本文所阐述的LDA算法全称为Latent Dirichlet Allocation&#xff08;网上没有标准的中文名称&#xff0c;我称之为潜在狄利克雷分配算法&#xff09;&#xff0c;不是线性判别分析算法&#xff08;Linear Discriminant Analysis&#xff09;。L…
阅读更多...
【机器学习】LDA算法原理

【机器学习】LDA算法原理

问题 线性判别分析（Linear Discriminant Analysis，LDA）是机器学习中常用的降维方法之一，本文旨在介绍LDA算法的思想，其数学推导过程可能会稍作简化。 LDA的思想 ● LDA是一种线性的、有监督的降维方法，即每个样本都有对应的类别标签（这点和PCA不同）。 ● 主要思想：…
阅读更多...
Spark机器学习-LDA算法09

Spark机器学习-LDA算法09

LDA算法 LDA即文档主题生成模型，该算法是一种无监督学习 将主题对应聚类中心，文档作为样本，则LDA也是一种聚类算法 该算法用来将多个文档划分为K个主题，与Kmeans类似 LDA是一种基于概率统计的生成算法 LDA算法—种常用的主题模型，可以对文档主题进行聚类，同样也可以用…
阅读更多...
LDA算法实现鸢尾花数据集降维

LDA算法实现鸢尾花数据集降维

目录 1. 作者介绍2. LDA降维算法2.1 基本概念2.2 算法流程 3. LDA算法实现3.1 数据集介绍3.2 代码实现3.3 结果展示 1. 作者介绍 唐杰&#xff0c;男&#xff0c;西安工程大学电子信息学院&#xff0c;2022级研究生 研究方向&#xff1a;机器视觉与人工智能 电子邮件&#xff…
阅读更多...
秒懂---LDA算法

秒懂---LDA算法

线性判别分析LDA原理总结 在主成分分析&#xff08;PCA&#xff09;原理总结中&#xff0c;我们对降维算法PCA做了总结。这里我们就对另外一种经典的降维方法线性判别分析&#xff08;Linear Discriminant Analysis, 以下简称LDA&#xff09;做一个总结。LDA在模式识别领域&…
阅读更多...
基于Sklearn实现LDA算法

基于Sklearn实现LDA算法

文章目录 一、LDA算法二、sklearn实现LDA三、结果如图四、总结五、参考 一、LDA算法 1.线性判别分析&#xff08;Linear Discriminant Analysis, LDA&#xff09;方法常被用于数据预处理中的降维&#xff08;dimensionality reduction&#xff09;步骤。LDA在保证良好的类别区…
阅读更多...
LDA算法推导

LDA算法推导

LDA算法是什么 简单地说LDA算法就是向低维度投影&#xff0c;让同一类别数据投影点更接近&#xff0c;不同类别数据点距离更远。 LDA原理 定义&#xff0c;已知 我们要把两类数据都投影到w直线上。 让不同类别的数据的类别中心之间的距离尽可能的大&#xff0c; 同一种类别数…
阅读更多...
线性判别分析LDA原理总结

线性判别分析LDA原理总结

转自http://www.cnblogs.com/pinard/p/6244265.html 在主成分分析&#xff08;PCA&#xff09;原理总结中&#xff0c;我们对降维算法PCA做了总结。这里我们就对另外一种经典的降维方法线性判别分析&#xff08;Linear Discriminant Analysis, 以下简称LDA&#xff09;做一个总…
阅读更多...
线性判别分析(Linear Discriminant Analysis, LDA）算法分析

线性判别分析(Linear Discriminant Analysis, LDA）算法分析

LDA算法入门 一． LDA算法概述： 线性判别式分析(Linear Discriminant Analysis, LDA)，也叫做Fisher线性判别(Fisher Linear Discriminant ,FLD)，是模式识别的经典算法，它是在1996年由Belhumeur引入模式识别和人工智能领域的。性鉴别分析的基本思想是将高维的模式样本投影到…
阅读更多...
机器学习笔记17-LDA算法

机器学习笔记17-LDA算法

1. LDA算法简介 LDA&#xff08;线性判别式分析 Linear Discriminant Analysis&#xff09;属于机器学习中的监督学习算法&#xff0c;常用来做特征提取、数据降维和任务分类。在人脸识别、人脸检测等领域发挥重要作用。LDA算法与PCA算法都是常用的降维技术。二者的区别在于&a…
阅读更多...
数据结构层次遍历二叉树

数据结构层次遍历二叉树

2022.11.19 计算二叉树的深度和节点个数 任务描述相关知识编程要求测试说明C/C代码 任务描述 本关任务&#xff1a;给定一棵二叉树&#xff0c;借助队列实现层次遍历二叉树。 相关知识 为了完成本关任务&#xff0c;你需要掌握&#xff1a;1.队列基本操作&#xff0c;2.二叉…
阅读更多...
树的层次遍历

树的层次遍历

二叉树的前序、中序、后序遍历我想大家应该都很熟悉了&#xff0c;那我们今天就来讲一下二叉树的层次遍历。 二叉树的前序、中序、后序遍历需要用到栈&#xff08;递归的过程也就是一个栈&#xff09;&#xff0c;层次遍历需要借助队列这个数据结构。 层次遍历的思路 我们给…
阅读更多...
层次遍历_树

层次遍历_树

哈喽大家好&#xff0c;这里是蒟蒻hanyiyang的博文&#xff0c;今天&#xff0c;我来给大家&#xff0c;介绍一个关于图的算法&#xff0c;希望能帮助到大家&#xff01;&#xff01;&#xff01; 层次遍历 大家来看一看上面这个图&#xff0c;为什么要说这是层次遍历呢&…
阅读更多...
树的应用 —— 二叉树的遍历【层次遍历、遍历序列还原树】

树的应用 —— 二叉树的遍历【层次遍历、遍历序列还原树】

树的应用 —— 二叉树的遍历【层次遍历、遍历序列还原树】 【层次遍历】 二叉树的遍历一般有先序遍历、中序遍历和后序遍历&#xff0c;除了这三种遍历&#xff0c;还有另一种遍历方式——层次遍历&#xff0c;即按照层次的顺序从左向右进行遍历。 一棵树如下图所示。 层次…
阅读更多...
二叉树：层次遍历算法（自上而下，从左到右）

二叉树：层次遍历算法（自上而下，从左到右）

层次遍历&#xff08;LevelOrder&#xff09;就是默认为自上而下&#xff0c;从左到右&#xff0c;一层一层进行遍历&#xff0c; 层次遍历需要借助队列来完成&#xff0c; 队列&#xff1a;先进先出&#xff08;FIFO&#xff09;。 分析&#xff1a;如图有一棵二叉树&#xff…
阅读更多...
推荐文章

Copyright @ 2022~2023