层序遍历？看这一篇就够了！

article/2025/9/18 19:45:01

点关注不迷路

1.树的层序遍历

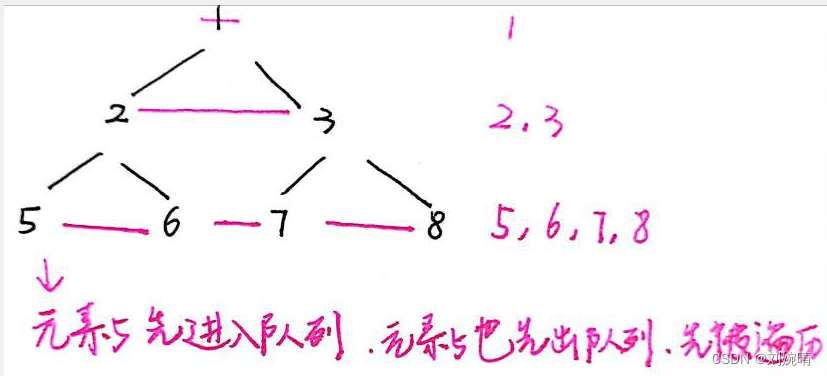
顾名思义，对于树型结构，层序遍历就是按层从上到下，每层按一定顺序对树的节点进行遍历。我们通过如图所示的二叉树进行说明：对于左边的二叉树，按层划分后可得到右边的分层结构。

如果按照每层从左到右的遍历逻辑，这棵二叉树的层序遍历序列就是 $[1, 4, 2, 7, 20, 5]$ 。通过代码如何实现呢？一般地，我们利用队列 $q u e u e$ 作为容器，按照如下逻辑进行遍历：

// 0. 声明队列
queue<TreeNode*> q;
// 1. 将根节点加入队列
q.push(root);
// 2. 遍历队列中每个节点
while(!q.empty()) {TreeNode* cur = q.front();q.pop();// 3. 记录当前节点值vec.push(cur->val);// 4. 将左右孩子放入队列q.push(cur->left);q.push(cur->right);
}

同一层中的节点自左向右遍历是通过队列实现的：还是拿之前的例子来说，先将值为 $1$ 的节点放入队列，然后将先左孩子 $4$ 放入队列，再将右孩子 $2$ 放入队列，由于队列是先进先出型结构，所以保证了值为 $4$ 的节点要先于值为 $2$ 的孩子处理；同样地，第三层节点放入队列的顺序依次为 $7, 20, 5$ ，与之后的处理顺序相同，保证了从左向右的顺序。过程如下图所示：(黄色代表加入队列的节点、粉色代表当前处理的节点、蓝色表示吃瓜的节点)

在这里插入图片描述

一般地，在遍历完第 $k$ 层的最后一个节点后，该层所有节点都被弹出了队列，且其孩子节点（均处于 $k + 1$ 层）都被存入了队列且未处理，所以当前队列的长度就是 $k + 1$ 层的节点数量。

所以，通过提前记录队列长度，可以方便地应对一些需要对各层进行特殊处理的问题。

特别地，为了防止二叉树为空、遍历到叶节点等情况，需要加入一些特判元素。修改后的模板如下：

// 1.初始化
queue<TreeNode*> q;
if(root == NULL) { // 二叉树为空return;
}
q.push(root);// 2.遍历整棵树
while(1) {int cnt = q.size(); // 要处理层的节点个数if(cnt == 0) break; // 已经遍历完二叉树// 3.遍历该层while(cnt--) {TreeNode* cur = q.front();q.pop();// 4.对 cur 的操作，根据题意更改action(cur);// 5.将左右孩子放入队列if(cur->left) q.push(cur->left);if(cur->right) q.push(cur->right);}
}

点关注不迷路

2.几道例题

说明：对于不同的题目，只需要在我们的模板基础上增加或更改一些元素，所以对于下面的每道例题，我们在代码中只重点注释修改的部分。

第一题：二叉树的层序遍历

我们先从基础的力扣102题来入手：题目要求返回一个二维容器，其中的每一个容器记录着某一层的所有节点值。我们只需要层序遍历二叉树，并按层遍历节点，将其加入 $v e c t o r$ 。在遍历完该层后，将记录了该层所有节点的 $v e c t o r$ 加入结果容器即可，代码如下：

  vector<vector<int>> levelOrder(TreeNode* root) {// 声明结果二维容器vector<vector<int>> result;queue<TreeNode*> q;if(root == NULL) return result;q.push(root);while(1) {int cnt = q.size();if(cnt == 0) break;// 记录该层节点的容器vector<int> v;while(cnt--) {TreeNode* cur = q.front();q.pop();// 将当前节点存入容器v.push_back(cur->val);if(cur->left) q.push(cur->left);if(cur->right) q.push(cur->right);}// 处理完该层，加入结果容器result.push_back(v);}return result;}

第二题：二叉树的层序遍历 II

与上一道题不同，要求从下到上遍历。实际上我们只需要从上向下遍历后，将结果容器翻转即可。C++的标准库STL给我们提供了容器翻转的函数：
$r e v e r s e (r e s u l t . b e g i n (), r e s u l t . e n d ())$

第三题：二叉树的锯齿形层序遍历

与前两题不同，对于给定的如图所示的树，锯齿形遍历需要偶数层从右向左返回结果，奇数层从左向右返回结果，也即返回的结果序列应为：

[[3],[20,9],[15,7]
]

本质上，我们只需要翻转偶数层的容器，就可以把从左向右的遍历转化为从右向左的遍历。在代码实现时，我们增加一个布尔型变量，记录当前层是否需要翻转，并每层将该变量取反即可：

vector<vector<int>> zigzagLevelOrder(TreeNode* root) {vector<vector<int>> result;// 当前层是否需要翻转bool flag = false;queue<TreeNode*> q;if(root == NULL) return result;q.push(root);while(1) {int cnt = q.size();if(cnt == 0) break;vector<int> v;while(cnt--) {TreeNode* cur = q.front();q.pop();v.push_back(cur->val);if(cur->left) q.push(cur->left);if(cur->right) q.push(cur->right);}// 判断是否翻转if(flag) reverse(v.begin(), v.end());result.push_back(v);// 取反flag = !flag;}return result;
}

第四题：二叉树的最大深度

这是力扣第104题，在我们的模板里，每处理完一层，才退出内层循环，并开始新一轮外层循环。而本题要找最大深度，就是找一共处理了多少层，所以提前维护一个记录层数的变量 $d e p t h$ ，然后在外层循环内每次增加该变量即可：

int maxDepth(TreeNode* root) {int depth = 0; // 声明深度queue<TreeNode*> q;if(root == NULL) return 0;q.push(root);while(1) {int cnt = q.size();if(cnt == 0) break;depth++; // 处理新一层前深度自加while(cnt--) {TreeNode* cur = q.front();q.pop();if(cur->left) q.push(cur->left);if(cur->right) q.push(cur->right);}}return depth;
}

特别地， $d e p t h + +$ 语句必须要放在判断 $c n t = 0$ 的语句之后，否则若遍历到最后一层，深度自加之后才会退出循环，导致结果错误。

第五题：二叉树的最小深度

第111题要求“最小深度”（找到离根节点最近的叶子节点），由于我们进行的是层序遍历，只要找到一个叶子节点，该节点就一定是所求的最近节点。所以，遍历过程中增加判断叶子节点的部分即可。来看看代码：

int minDepth(TreeNode* root) {int depth = 0;queue<TreeNode*> q;if(root == NULL) return 0;q.push(root);while(1) {int cnt = q.size();if(cnt == 0) break;depth++;while(cnt--) {TreeNode* cur = q.front();q.pop();// 叶子节点if(!cur->left && !cur->right) return depth;if(cur->left) q.push(cur->left);if(cur->right) q.push(cur->right);}}return depth;
}