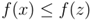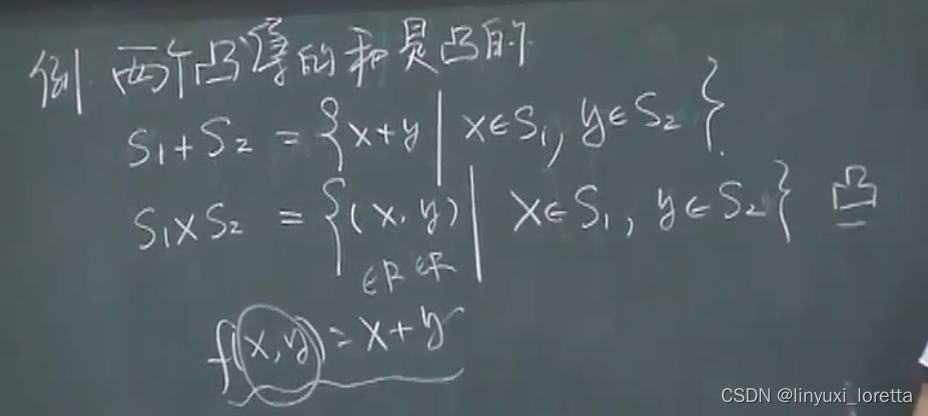定义函数,存在多个局部极小值,建议在局部优化之前进行全局优化,缩小范围
def fm(p):x, y = preturn (np.sin(x) + 0.05 * x ** 2+ np.sin(y) + 0.05 * y ** 2)
x = np.linspace(-10, 10, 50)
y = np.linspace(-10, 10, 50)
X, Y = np.meshgrid(x, y)
Z = fm((X, Y))
fig = plt.figure(figsize=(10, 6))
ax = fig.gca(projection='3d')
surf = ax.plot_surface(X, Y, Z, rstride=2, cstride=2,cmap='coolwarm', linewidth=0.5,antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')
fig.colorbar(surf, shrink=0.5, aspect=5)
全局优化
给定x,y的范围(-10,-5,0,5,10),最优化参数值是x=,0y=0
import scipy.optimize as sco
def fo(p):x, y = pz = np.sin(x) + 0.05 * x ** 2 + np.sin(y) + 0.05 * y ** 2if output == True:print('%8.4f | %8.4f | %8.4f' % (x, y, z)) return z
output = True
sco.brute(fo, ((-10, 10.1, 5), (-10, 10.1, 5)), finish=None)
#array([ 0., 0.])调整步长为0.1,最优化参数值是x=-1.4,y=-1,4,最小值-1.77
output = False
opt1 = sco.brute(fo, ((-10, 10.1, 0.1), (-10, 10.1, 0.1)), finish=None)
opt1
#array([-1.4, -1.4])
fm(opt1)
#-1.7748994599769203局部优化
opt2 = sco.fmin(fo, opt1, xtol=0.001, ftol=0.001,maxiter=15, maxfun=20)
opt2
#array([-1.42702972, -1.42876755])
fm(opt2)
#-1.7757246992239009约束优化
def Eu(p): s, b = preturn -(0.5 * math.sqrt(s * 15 + b * 5) +0.5 * math.sqrt(s * 5 + b * 12))
cons = ({'type': 'ineq','fun': lambda p: 100 - p[0] * 10 - p[1] * 10}) #约束条件
bnds = ((0, 1000), (0, 1000))
result = sco.minimize(Eu, [5, 5], method='SLSQP',bounds=bnds, constraints=cons) #初始值5,5
result['x']
#array([ 8.02547122, 1.97452878])
-result['fun']
#最优函数值9.700883611487832
np.dot(result['x'], [10, 10]) #验证