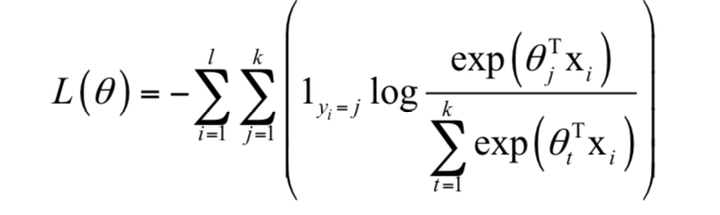凸优化学习

article/2025/10/16 22:39:34

”凸优化“ 是指一种比较特殊的优化，是指求取最小值的目标函数为凸函数的一类优化问题。凸优化就是：1、在最小化（最大化）的要求下，2、目标函数是一个凸函数（凹函数），3、同时约束条件所形成的可行域集合是一个凸集。其中，目标函数为凸函数且定义域为凸集的优化问题称为无约束凸优化问题。而目标函数和不等式约束函数均为凸函数，等式约束函数为仿射函数，并且定义域为凸集的优化问题为约束优化问题。

一个集合

称为凸集，若对任意的两个点

,连接他们的两个点所在的直线都在集合

内。即，

一般可见的集合都是凸集，例如单位球体。

优化问题转换为凸优化的方法：

对偶（Duality）是每个学习运筹学或者凸优化的人都必须熟练掌握的方法，对偶有很多种，本科运筹就教会大家写一个线性规划的对偶形式，高等数学里面也会提到用到拉格朗日乘子之类的约束优化问题，也即解拉格朗日对偶或者KKT条件。一般的，对于许多非凸优化的问题，我们仍然可以写出它的拉格朗日对偶。如原问题如下 $\{\min_{x}f(x),\ \text{s.t.}\ g_i(x)\geq 0\}$ ，拉格朗日对偶为 $\max_{\lambda\geq 0}\min_{x}f(x)-\lambda^Tg(x)$ ，其中 $\ g(x)=(g_1(x)...g_n(x))^T$ 。可以看到 $f(x)-\lambda^Tg(x)$ 是关于 $\lambda$ 的线性函数，因此 $\min_{x}f(x)-\lambda^Tg(x)$ 一定是一个关于 $\lambda$ 的凹函数。因此，由我们之前给的定义来看，拉格朗日对偶永远都是一个关于对偶变量的凸优化问题，并且根据弱对偶定理，可以给出原问题的下界。

松弛（Relaxation）也是常用的方法之一，在第一点里，我们举了一些例子可以通过松弛，去掉整数约束，使其等价为凸优化。通常情况下，我们松弛原问题，只能得到一个可行域更大的问题，如果原问题是求最小，则松弛后的问题的最优值一定小于等于原问题的最优值，这也是一种给出下界的方法。松弛不仅仅用于整数约束，只要利于将可行域非凸变为凸集皆可。例如，某问题有一约束为 $x^2+bx+c=0$ ，就不构成一个凸集，但等价于 $x^2+bx+c\leq 0$ 和 $x^2+bx+c\geq 0$ ，前一个不等式即构成凸集，因此我们可以将后一个不等式从约束中去除，就得到原问题的一个凸优化松弛问题。