目录

 

凸优化概述

1 概述

2 凸集

3 凸方法

3.1 凸性的一阶条件

3.2 凸性的二阶条件

3.3 詹森不等式

3.4 分段集

4 凸优化问题

---

凸优化概述

1 概述

也就是说，给定一个函数，我们想找到使最小化(或最大化)。目前已有的方法包含：最小二乘、逻辑回归和支持向量机。然而，对于一类特殊的优化问题称为凸优化问题，我们可以在很多情况下有效地找到全局解。

2 凸集

定义2.1：一组C是凸,如果任何x, y∈C和θ∈R与0≤θ≤1，

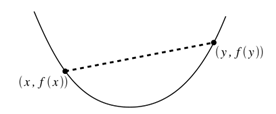
直观地，考虑这个定义的方法是如果我们在凸函数的图上取任意两点并在两点之间画一条直线，那么函数在这两点之间的部分就会在这条直线下面

3 凸方法

定义3.1：函数是凸函数，如果其域(表示D (f))是一个凸集,如果x, y∈D (f)和θ∈R, 0≤θ≤1,

直观地，考虑这个定义的方法是如果我们在凸函数的图上取任意两点并在两点之间画一条直线，那么函数在这两点之间的部分就会在这条直线下面

 

 

3.1 凸性的一阶条件

假设函数 是可微的。梯度 存在所有点x在域f中。那么f是凸函数当且仅当D (f)是一个凸集,x, y∈D (f)，

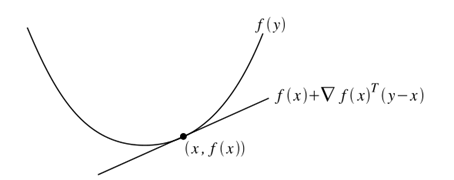
函数 称为在点x处的一阶近似函数f。直觉上看，这可以近似认为是在点x处的切线。凸性的一阶条件说，f是凸函数当且仅当函数的切线是全局上低于f值的。换句话说,如果我们把方法上的任意一点画切线，那么这条直线上的每一点将低于相应的函数值。

3.2 凸性的二阶条件

假设函数 是二次可微的。 被定义为所有点x的域f)。那么f是凸函当且仅当D (f)是一个凸集及其 半正定：即对于任意x∈D(f)，

这里，符号 当与矩阵结合使用时，指的是正半虚数性，而不是成分不等式。在一维中，这等价于二阶导数f " (x)总是非负的条件(函数始终为正非负)。

3.3 詹森不等式

假设我们从凸函数的基本定义中的不等式开始

使用归纳法，这可以很容易地扩展到多个点的凸组合，

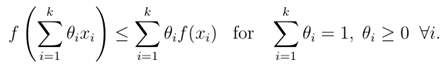
事实上，这也可以推广到无穷和或积分。在后一种情况下，不等式可以写成：

由于p(x)积分为1，通常把它看作概率密度，在这种情况下，前面的方程可以用期望来表示：

最后一个不等式叫做Jensen不等式。

3.4 分段集

凸函数产生一种特别重要的凸集称为α-sublevel集。给出了凸函数 和一个实数α∈R,α-sublevel集被定义为

换句话说,α-sublevel集是所有点的集合x, f (x)≤α。

表明这是一个凸集,考虑任何x, y∈D (f), f (x)≤α和f (y)≤α。然后

4 凸优化问题

其中f为凸函数，C为凸集，x为优化变量。然而，由于这可能有点模糊，我们通常把它写成：

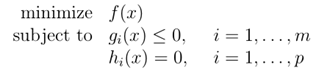
其中f为凸函数， 为凸函数， 为仿射函数，x为优化变量。

注意这些不等式的方向是否重要:凸函数 必须小于零。这是因为 的0个子空间集是一个凸集，所以可行域(许多凸集的交集)也是凸的(记住仿射子空间也是凸集)。如果我们要求某个凸的 ≥0，那么可行域就不再是凸集，我们用来求解这些问题的算法也不再保证能找到全局最优解。还要注意，只有仿射函数才允许为等式约束。直观地，你可以认为这是因为一个等式约束等价于两个不等式 ≤0和 ≥0。然而，当且仅当 同时为凸和凹时， 一定是仿射。

优化问题的最优值是表示p⋆(有时f⋆)并且它等于目标函数在可行域内的最小可能值

定义4.1： x是局部最优的，如果它是可行的（它满足优化问题的限制），如果存在R>0使得所有可行的点z当满足

定义4.2：一个点x是全局最优的，如果它是可行的，对于所有可行点z，

对于一个凸优化问题，所有局部最优点都是全局最优的。

-------------------------------------------------------------------------------------------------------------------------

参考资料：

1、Convex Optimization Overview：

https://web.stanford.edu/class/archive/cs/cs224n/cs224n.1184/readings/cs229-cvxopt.pdf

2、http://cs231n.github.io/optimization-1/